Примеры решения задач по статистической физике и термодинамике

Задача 1. В сосуде объемом V₁ = 3 л находится газ под давлением 0,2 МПа, в другом сосуде объемом V₂ = 4 л находится тот же газ под давлением 0,1 МПа. Температура в обоих сосудах одинакова. Под каким давлением будет находиться газ, если сосуды соединить трубкой?

Дано: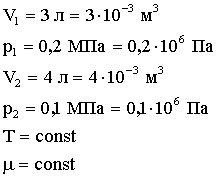
Найти:	р

Решение: По закону Дальтона:

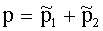(1)

где 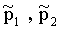- парциальные давления.

Из уравнения Менделеева-Клапейрона до соединения сосудов получим:

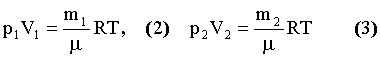
где m₁ и m₂ - масса газа в первом и во втором сосудах;
μ - молярная масса;
R - газовая постоянная.

Аналогично для парциальных давлений (после соединения):

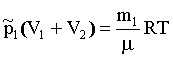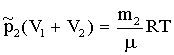(4) и (5)

Так как T = const и μ = const, то правые части уравнений (2) и (4), а также уравнений (3) и (5) равны. Тогда:

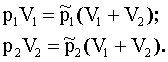
Отсюда:

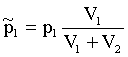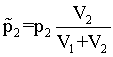(6) и (7)

Подставляя (6) и (7) в (1), получим:

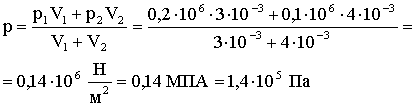
Ответ: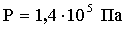

Задача 2. Какая часть молекул кислорода при температуре Т = 273 К обладает скоростями, лежащими в интервале от v₁ = 100 м/с до v₂ = 110 м/c? Чему равна наиболее вероятная скорость движения молекул?

Дано: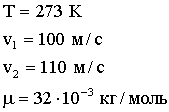
Найти: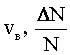

Решение: Найдем наиболее вероятную скорость молекул:

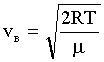
где R - газовая постоянная,
μ - молярная масса.

Подставим численные значения:

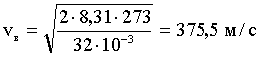
Интервал скоростей: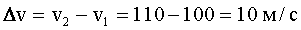

Это много меньше v₁ и v₂. Поэтому можно использовать приближенную формулу:

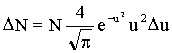(1)

где ΔN - число частиц, обладающих скоростями в интервале от v₁ до v₂ ,
N - полное число частиц,

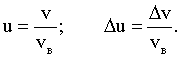
Относительное число частиц или доля молекул, обладающих скоростями в заданном интервале, найдем из формулы (1) при :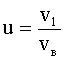

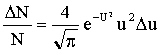(2)

Вычислим: 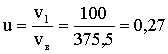, подставим в (2) и учтем, что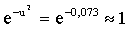

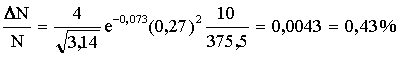
Ответ: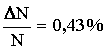

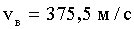
Задача 3. Определить среднюю длину свободного пробега молекул и число соударений за 1 с, происходящих между всеми молекулами кислорода, находящегося в сосуде емкостью 2 л при температуре 27^оС и давлении 100 кПа.

Дано: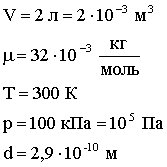
Найти:	< λ >, z

Решение: Средняя длина свободного пробега молекул вычисляется по формуле:

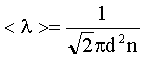(1)

где d - эффективный диаметр,
n - концентрация, т.е. число молекул в единице объема.

Давление связано с концентрацией:

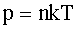
где k - постоянная Больцмана.

Выразим n:

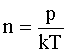(2)

Подставим (2) в (1) и получим:

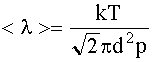(3)

Число соударений, происходящих между всеми молекулами за 1 с равно:

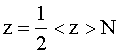(4)

где N - число молекул в сосуде объемом V,
< z > - среднее число соударений одной молекулы за 1 с.

Число молекул в сосуде равно:

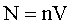(5)

Среднее число соударений молекулы за 1 с:

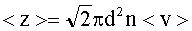(6)

где < v > - средняя арифметическая скорость молекулы.

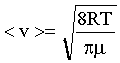(7)

Подставим в (4) выражения (5), (6), (7):

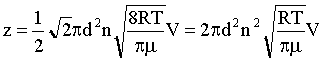
Учтем (2):

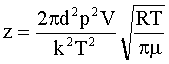
Подставим численные значения:

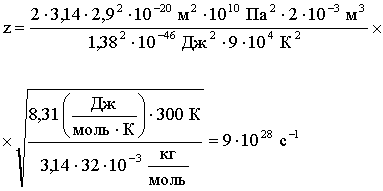
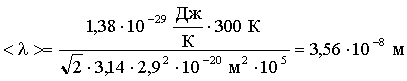
Ответ: z = 9·10²⁸ с-1, < λ > = 3,56·10^-8 м.

Задача 4. Горячая вода некоторой массы отдает теплоту холодной воде такой же массы и температуры их становятся одинаковыми. Показать, что энтропия при этом увеличивается.

Решение: Обозначим температуру горячей воды Т₁, холодной Т₂, а температуру смеси Q. Определим температуру смеси, исходя из уравнения теплового баланса.

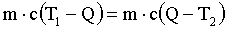
где с - удельная теплоемкость, m - масса.

Тогда: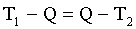

Отсюда температура смеси равна:

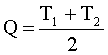(1)

Изменение энтропии, происходящее при охлаждении горячей воды:

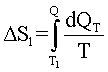
Элементарное количество теплоты равно:

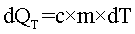
Тогда:

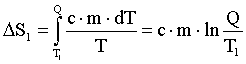
Изменение энтропии, происходящее при нагревании холодной воды:

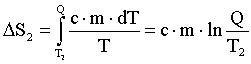
Изменение энтропии системы равно:

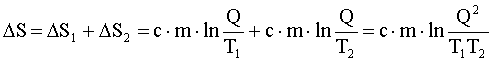
С учетом (1) получим:

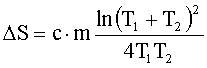
Так как 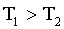, то 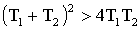, следовательно: 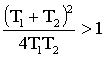и .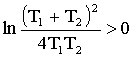
Тогда 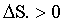, т.е. энтропия возрастает.

Квантовая физика