Электростатика. Постоянный электрический ток.

Электромагнетизм.

Электрическое поле. Электрический заряд. Закон Кулона. Напряженность поля. Принцип суперпозиции полей. Диполь.

Вектор индукции электростатического поля. Поток вектора индукции. Теорема Гаусса. Расчет полей равномерно заряженных проводников. Работа электростатического поля. Потенциал электрического поля. Связь между напряженностью и потенциалом. Циркуляция вектора напряженности электростатического поля.

Проводники в электрическом поле. Электростатическая индукция. Поверхностная плотность заряда. Диэлектрики в электрическом поле. Вектор поляризации, поляризационные заряды, диэлектрическая проницаемость.

Электроемкость. Конденсаторы. Расчет конденсаторов различной конфигурации. Соединения конденсаторов. Энергия конденсаторов.

Основные понятия об электрическом токе. Закон Ома для однородного участка цепи в интегральном и дифференциальном виде. Закон Джоуля-Ленца. Законы постоянного тока. Законы Ома для неоднородного участка цепи, для полной цепи. Законы Кирхгофа. Электронная теория проводимости металлов. Ток в полупроводниках. Ток в вакууме. Работа выхода электронов из металла. Контактная разность потенциалов в металле. Явление Зеебека. Ток в жидкости. Законы Фарадея. Электролиз в технике.

Раздел IV. Электродинамика Оптика. Атомная и ядерная физика.

Магнитное поле тока. Магнитная индукция. Закон Био-Савара-Лапласа. Расчет магнитного поля проводников различных конфигураций. Теорема о циркуляции вектора магнитной индукции. Поток вектора магнитной индукции.

• Закон Ампера. Работа сил Ампера. Сила Лоренца. Магнитное поле в веществе. Диа-, пара-, ферромагнетики. Вектор намагниченности, магнитная проницаемость. Напряженность магнитного поля. Объяснение "петли гистерезиса" для ферромагнетиков. Точка Кюри.

• Электромагнитная индукция. ЭДС в движущихся проводниках. Закон Ленца.

• Самоиндукция. Энергия магнитного поля.

• Колебательный контур. Свободные электрические колебания. Формула Томсона.

• Переменный ток. Активное, индуктивное и емкостное сопротивления. Закон Ома для цепей переменного тока. Трансформаторы.

• Электромагнитные волны и их свойства. Шкала электромагнитных волн

• Световые волны. Законы прямолинейного распространения света, отражения, преломления. Тонкие линзы. Формула тонкой линзы.

• Интерференция света. Тонкие пленки. Опыт Юнга.

• Дифракция света. Дифракция от одной щели. Дифракционная решетка. Разрешающая способность дифракционной решетки.

• Дисперсия света. Спектроскопия.

• Поляризация света. Законы Брюстера, Малюса.

Давление света. Фотоэффект. Законы Столетова, Эйнштейна для фотоэффекта.

• Планетарная модель атома и ее трудности. Модель атома Резерфорда-Бора.

• Радиоактивные превращения. Закон радиоактивного распада. Методы регистрации элементарных частиц. Строение ядра. Ядерные силы. Энергия связи. Физические основы ядерной энергетики.

ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК

Электростатика

Закон Кулона ,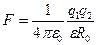

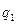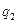где F – сила взаимодействия двух точечных зарядов и ; R – расстояние между зарядами; 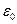- электрическая постоянная; 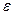- диэлектрическая проницаемость среды.

Напряженность электрического тока 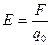, где F – сила, действующая на заряд 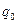, находящийся в данной точке поля.

Напряженность поля:

а) точечного заряда: 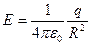, где R – расстояние от заряда q до точки, в которой определяются напряженность и потенциал;

б) диполя: 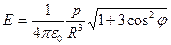, где p=ql (момент диполя); 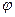- угол между расстоянием от центра диполя до точки наблюдения R и длиной l диполя;

в) вне сферы: 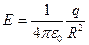, где R – расстояние от центра сферы;

внутри сферы: E=0;

г) бесконечно длинной нити: 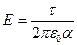, где 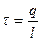- линейная плотность заряда; l – длина нити; 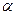- расстояние от нити до точки, в которой вычисляется напряженность поля.

д) бесконечной плоскости: 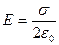, где ,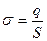

где S – площадь поверхности, по которой распределен заряд;

е) двух бесконечных плоскостей: , .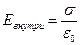

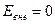Электрическая индукция .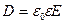

Теорема Гаусса: 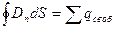; где 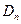- проекция вектора D на направление нормали к элементу поверхности, площадь которой равна dS; 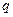- заряды, охватываемые поверхностью.

Электроемкость 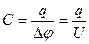, 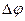- изменение потенциала, вызванное зарядом q.

Электроемкость

а) плоского конденсатора: 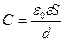, где S – площадь пластин конденсатора; d – расстояние между ними; 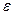- диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

б) параллельно соединенных конденсаторов: ,

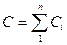в) последовательно соединенных конденсаторов: .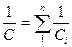

Энергия электрического поля , , .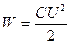

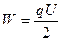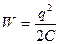Объемная плотность энергии , , .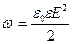

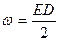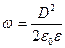Постоянный ток

Сила тока 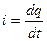, , 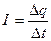где q – количество электричества, прошедшее через поперечное сечение проводника за время t.

Плотность тока: 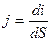, , 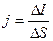где S – площадь поперечного сечения.

Закон Ома: 1) для однородного участка цепи 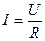, , 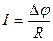где R – сопротивление участка цепи; 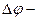разность потенциалов.

2) для неоднородного участка цепи ,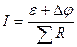

3) для замкнутой цепи 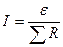, где R – сопротивление цепи; 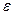- ЭДС источника тока.

Законы Кирхгофа:

1) для токов, сходящихся в узле .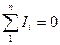

2)для замкнутого контура .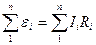

Работа и мощность тока

Для участка цепи: , , .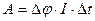

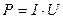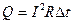Для полной цепи , .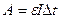

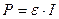МАГНИТНОЕ ПОЛЕ В ВАКУУМЕ

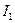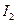
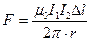Сила взаимодействия прямых параллельных токов и , где 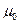- магнитная постоянная; 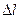- длина участка проводника, на который действует сила; r – расстояние между проводниками.

Сила Ампера, действующая на проводник с током в магнитном поле,

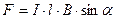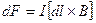, , где l – длина проводника; B –магнитная индукция поля; 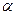- угол между векторами l и B.

Сила Лоренца, действующая на заряженную частицу q, движущуюся со скоростью 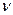в магнитном поле с индукцией B:

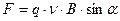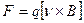, , где 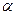- угол между векторам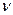и и .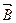

Закон Био-Савара-Лапласа: 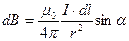, где dl – длина проводника, r – расстояние от середины элемента проводника до точки, магнитная индукция в которой определяется, 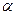- угол между dl и r.

Магнитная индукция, созданная

1.прямолинейным проводником на расстоянии r .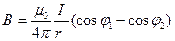

2. круговым током в центре 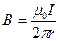, где r – радиус кривизны проводника;

3. бесконечно длинным проводником 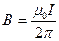, где r-расстояние от оси проводни­ка;

4. длинным соленоидом на оси 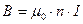, где 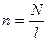, где N - число витков; l - длина проводника; I - сила тока в одном витке.

Поток вектора магнитной индукции через плоский контур площадью S

, .

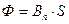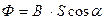Работа сил магнитного поля ,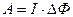

Закон Фарадея для электромагнитной индукции ,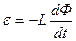

для самоиндукции 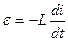, где L - индуктивность контура.

Количество заряда, протекающего через сопротивление R при изменении маг­нитного потока ,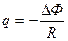

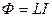
Индуктивность длинного соленоида , , .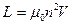

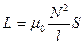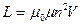Экстраток замыкания и размыкания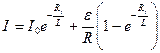

при замыкании 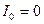, при размыкании .

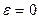Энергия магнитного поля .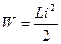

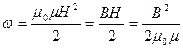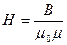Объемная плотность энергии , где - напряженность магнитного поля.

ОПТИКА

Закон преломления света 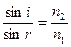, , 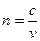где i - угол падения; r - угол преломления; 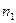и 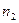- абсолютные показатели преломления соответственно первой и второй сред; с - скорость света в вакууме; 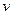- скорость света в среде.

Формула тонкой линзы 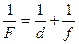, где F - фокусное расстояние линзы; d- расстояние от оптического центра линзы до предмета; 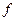- расстояние от оптического центра линзы до изображения.

Оптическая сила: 1) линзы ,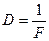

2) системы линз .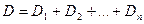

Интерференционный max: ,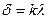

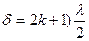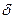интерференционный min: , где - оптическая разность хода, 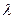- длина волны.

Расстояние между интерференционными полосами, полученными от 2-х когерентных источников 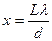, L - оптическая длина пути световой волны.

Оптическая разность хода для тонкой пластинки при отражении .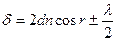

В отраженном свете: радиус темных колец Ньютона ,;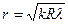

радиус светлых колец Ньютона 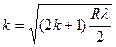, где R - радиус кривизны поверхности линзы, соприкасающейся с плоскопараллельной стеклянной пластинкой.

Условие дифракции на щели 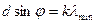, , 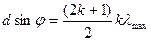где d - ширина щели, 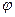- угол дифракции.

Условие главного max для дифракционной решетки .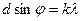

Разрешающая способность спектрального прибора ,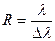

где 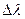- наименьшая разность длин волн двух соседних спектральных лини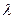й ( и 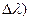, при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки;

для диф. Решетки 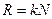, где N - число штрихов решетки.

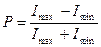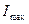Степень поляризации , где и 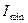- максимальная и минимальная интенсивности частично поляризованного света, пропускаемого анализатором.

Закон Брюстера при отражении: 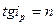, где 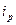- угол падения, при котором отраженная световая волна полностью поляризована, n - относительный показатель преломления.

Закон Малюса: а) 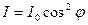(без поглощения);

б) 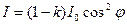(k - коэффициент поглощения), где I- интенсивность плоскополяризованного света, прошедшего через анализатор; 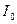- интенсивность плоскополяризованного света, падающего на анализатор; 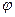- угол между направлением колебаний светового вектора волны, падающей на анализатор, и плоскостью пропускания анализатора.

Квантовая оптика

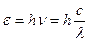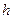Энергия фотона . где - постоянная Планка; 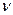- частота света; 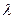- длина волны.

Масса и импульс фотона , .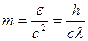

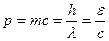Уравнение Эйнштейна для фотоэффекта 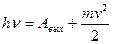, где А - работа выхода электронов из металла.

"Красная граница" фотоэффекта .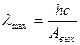

Давление света 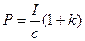, где I - облученность поверхности; k - коэффициент отражения.

Изменение длины волны рентгеновских лучей при рассеянии их на электроне: на угол 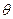(комптоновское рассеяние):

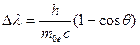, где 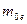- масса электрона отдачи.

СТРОЕНИЕ АТОМА И ЯДРА

Полная энергия электрона на n-ой орбите атома с зарядом ядра z

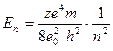, или 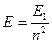, где m - масса электрона; 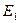- энергия ионизации атома; n - главное квантовое число.

Энергия, излучаемая или поглощаемая атомом водорода (водородоподобного атома) при переходе из одного стационарного состояния в друго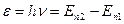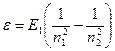е: , , где 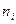- номер серии спектральных линий.

Масса релятивистской частицы: ,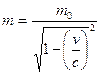

полная энергия: .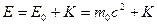

Кинетическая энергия релятивистской частицы: ,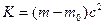

.

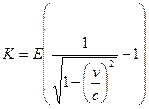Связь между полной энергией и импульсом релятивистской частицы

.

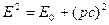Радиоактивность

Закон радиоактивного распада: 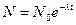, где N - число нераспавшихся атомов в момент времени t; 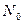- число нераспавшихся атомов в момент, принятый за начальный (t=0); е - основание натуральных логарифмов; 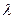- постоянная радиоактивного распада.

Число ядер, распавшихся за время :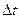

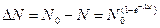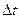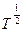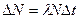при << , , где 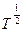- период полураспада.

Период полураспада: .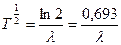

Среднее время жизни ядра: .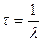

Активность радиоактивного распада , .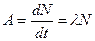

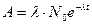Ядерная реакция: 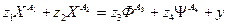, где 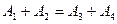, , 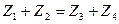где у - энергетический эффект реакции.

Дефект массы ядра .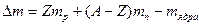

Энергия связи атомного ядра 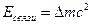или 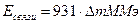Удельная энергия связи 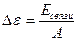, А - число нуклонов в ядре;

.

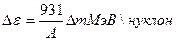Примеры решения задач

Пример 1. Два точечных электрических заряда 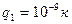и 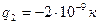находятся в воздухе на расстоянии d=10 см друг от друга. Определить напряженность и потенциал поля, создаваемого этими зарядами в точке A, если расстояние 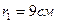и .

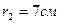Решение. Общая (результирующая) напряженность Е в точке А равна сумме напряженностей двух полей, создаваемых зарядам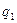и и 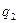, т. е.

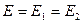, (1) где 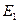— напряженность поля заряда 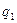; Е₂ — напряженность поля заря .

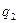На рисунке вектор 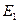направлен от заряда 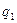, так как этот заряд положительный, вектор 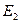направлен сторону заряда q₂, так как этот заряд отрицательный. Результирующий вектор Е совпадает по величине и направлению с диагональю параллелограмма, построенного на слагаемых векторах. Абсолютное значение этого вектора найдем из соотношения:

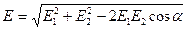. (2)

Абсолютную величину напряженносте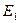й и 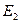, а также 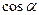определим по формулам:

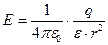, (3)

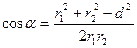. (4)

Выразим числовые значения всех величин в единицах СИ:

, , ,

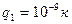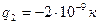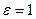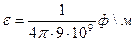
Подставив эти числовые значения в формулы (3), (4)и (2), получим:

.

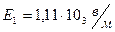
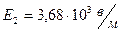При вычислении 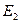знак заряда q₂ был опущен, так как в данном случае важно знать абсолютное значение напряженности

.

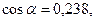
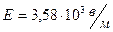Потенциал 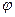результирующего поля, созданного двумя зарядам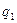и и 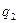равен алгебраической сумме потенциалов, т. е.

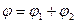(5)

Потенциал 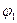является положительным, так как поле создано положительным зарядом 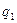потенциал 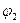является отрицательным,: так как поле создано отрицательным зарядом .

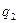Потенциал поля, созданного точечным зарядом, определяется по формуле:

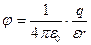(6)

Подставив сюда численные значения величин, получим: .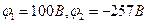

Пример 2. Определить начальную скорость 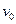сближения протонов, находящихся на достаточно большом расстоянии друг от друга, если минимальное расстояние 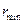, на которое они могут сблизиться, равно 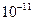.см

Решение. Между двумя протонами действуют силы отталкивания, вследствие чего движение протонов будет замедленным. Поэтому задачу можно решить как в инерциальной системе координат (связанной с центром масс двух протонов ), так и в неинерциальной (связанных с одним из ускоренно движущихся протонов). Во втором случае законы Ньютона не имеют места. Применение же принципа Даламбера затруднительно из-за того, что ускорение системы будет переменным. Поэтому удобно рассмотреть задачу в инерциальной системе отсчета.

Поместим начало координат в центре масс протонов. Поскольку мы имеем дело с одинаковыми частицами, то центр масс будет находиться в точке, делящий пополам отрезок, соединяющий частицы. Относительно центра масс частицы будут иметь в любой момент времени одинаковые по абсолютной величине скорост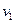и и 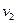. Скорость каждой частицы будет равна половине скорости сближения

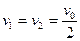. (1)

В дальнейшем воспользуемся законом сохранения энергии, записанную в виде

Т+П=const,

Где 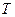– кинетическая энергия, 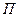– потенциальная энергия.

Выразим потенциальную энергию в начальный и конечный моменты движения.

В начальный момент. Согласно условию задачи, протоны находились на большом расстоянии, поэтому потенциальной энергии можно пренебречь. Следовательно, для начального момента полная энергия будет равна кинетической энергии 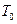протонов, т.е. 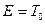. (2)

В конечный момент, когда протоны максимально сблизится, скорость и кинетическая энергия равны нулю, а полная энергия 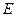будет равна потенциальной энергии 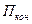: 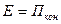. (3)

Приравнивая правые части равенств (2) и (3), получим: 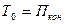. (4)

Кинетическая энергия 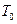равна сумме кинетических энергии протонов:

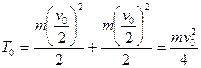(6)

потенциальная энергия системы двух зарядов 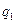и 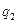, находящихся в вакууме, определяется по формул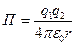е: , где 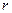– расстояние между зарядами.

Воспользовавшись этой формулой. Получим: 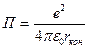. (6)

С учетом выражений (5) и (6) формула (4) примет вид: .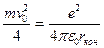

Откуда: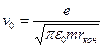

Подставив числовые значения. Получим: .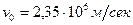

Пример 3. Электрон со скоростью 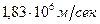влетел однородное электрическое поле в направлении, противоположном напряженности поля. Какую разность потенциалов должен пройти электрон, чтобы обладать энергий 13,6 эв? (Обладая такой энергии, электрон, при столкновении с атомом водорода, может ионизировать его. Энергия 13,6 эв называется энергией ионизации водорода).

. Решение. Электрон должен пройти такую разность потенциалов U, чтобы приобретенная при этом энергия W в сумме с кинетической энергией Т, которой обладал электрон перед вхождением в поле, составила энергию, равную энергии ионизации 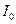. т.е.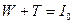

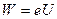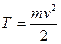Выразив в этой формуле и , получим: .

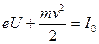Отсюда: .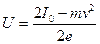

Произведя вычисления в единицах СИ, получим: .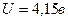

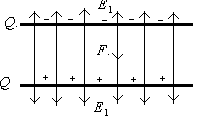
Пример 4. На пластинках плоского конденсатора находится заряд. 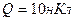Площадь 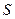каждой пластины конденсатора равна 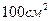, диэлектрик – воздух. Определить силу 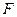, с которой притягиваются пластины. Поле между пластинами считать однородным.

Решение.Заряд 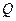одной пластины находится в поле напряженностью 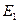, созданным зарядом другой пластины конденсатора. Следовательно, на первый заряд действует сила (см.рис.)

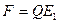(1)

Так как 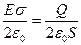, (2)где 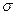– поверхностная плотность заряда пластины, то формула (1) примет вид: .

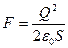Произведя вычисления, находим: .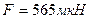

Пример 5. По длинному прямому тонкому проводу течет ток силой 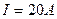. Определить магнитную индукцию В поля, создаваемого проводником в точке, удаленной от него на расстояние .

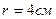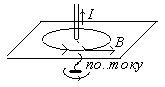Решение.Магнитное поле, создаваемое прямым бесконечно длинным проводником ничтожно малого сечения, обладает осевой симметрией. Это значит, что модуль вектора магнитной индукции в данной точке будет зависеть только от ее расстояния до проводника. Поэтому все точки на окружности радиусом (см. рис.) лежащий в плоскости, перпендикулярной проводнику, будут характеризоваться одинаковой по модулю магнитной индукцией: 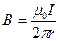, (1) где 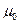– магнитная постоянная.

Направление вектора В зависит от положения точки на окружности и направления тока в проводнике. Этот вектор направлен по касательной к проведенной нами окружности (это следует из закона Био-Савара – Лапласа, записанного в векторной форме). Окружность на рис. является магнитной силовой линией. Ее направление (а значит, и направление вектора В) определяется по правилу правого винта.

Произведя вычисления находим В=0,1мТл.

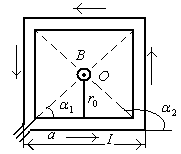Пример 6. По проводу, согнутому в виде квадрата со стороной, а=10см, течет ток силой 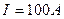. Найти магнитную индукцию В в точке О пересечения диагоналей квадрата.

Решение.Расположим квадратный виток в плоскости чертежа. Согласно принципу суперпозиции магнитных полей 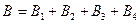, (1) где 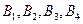- магнитные индукции полей, создаваемых токами, протекающими по каждой стороне квадрата.

В точке О пересечения диагоналей квадрата все векторы индукции будут направлены перпендикулярно плоскости витка «к нам». Кроме того, из соображений симметрии следует, что модули этих векторов одинаковы: 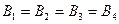. Это позволяет векторное равенство (1) заменить скалярным : 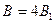. (2)

Магнитная индукция поля, создаваемого отрезком прямолинейного провода с током, выражается формулой:

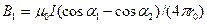. (3)

Учитывая, что 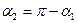и 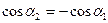(см. рис.), формулу (3)можно переписать в виде: .

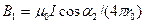Подставив выражение 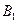в формулу (2), найдем .

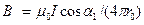Заметив, что 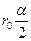и 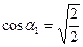(так как 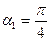), получим :

.

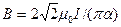Подставляя численные значения, получим: В=1,13мТл.

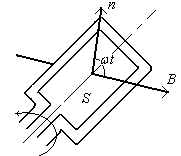
Пример 7. В однородном магнитном поле (В=0,1Тл) равномерно с частотой 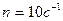вращается рамка, содержащая 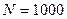витков, плотно прилегающих друг к другу. Площадь 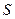рамки равна 150см. Определить мгновенное значение э.д.с. индукции 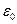соответствующее углу 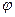поворота рамки, равному .

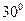Решение.Мгновенное значение э.д.с. индукции 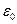определяется основным уравнением электромагнитной индукции Фарадея – Максвелла:

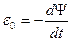, (1)где 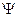– потокосцепление.

Потокосцепление 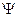связано с магнитным потоком Ф и числом 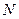витков, плотно прилегающих друг к другу, соотношением: 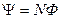. (2)

Подставляя выражение 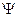в формулу (1), получаем: 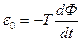. (3)

При вращении рамки (см. рис.) магнитный поток Ф, пронизывающий рамку в момент времени 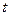, определяется соотношением: 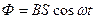, где В – магнитная индукция, S– площадь рамки, 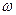– круговая (или циклическая частота).

Подставив в формулу (2) выражение Ф и продифференцировав полученное выражение по времени, найдем мгновенное значение э.д.с. индукции:

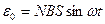(4)

круговая частота 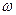связана с частотой вращения 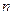соотношением .

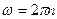Подставляя выражение 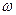в формулу (3) и заменив 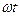на 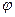, получим: .

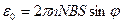Подставляя численные значения получим: .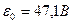

Пример 8. Соленоид с сердечником из намагниченного материала содержит 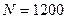витков провода, плотно прилегающих друг к другу. При силе тока 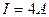магнитный поток 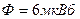. Определить индуктивность 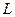соленоида и энергию 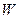магнитного поля соленоида.

Решение. Индуктивность 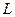связана с потокосцеплением 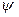и силой тока 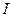соотношением: 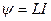. (1)

Потокосцепление. в свою очередь, может быть определено через поток Ф и число витков 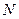(при условии, что витки плотно прилегают друг к другу): 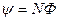. (2)

Из формул (1) и (2) находим индуктивность соленоида:

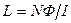. (3)

Энергия магнитного поля соленоида: 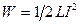. Выразив 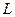согласно формуле (3) получим: . еских величин и произведем вычисления: у. е значение радея – Максвелла:

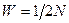
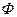
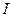. (4)

Подставим в формулы (3) и (4) значения физических величин и произведем вычисления: , .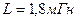

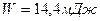Пример 9. От двух когерентных источников 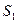и 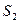( 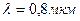) лучи попадают на экран. На экране наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему поместили мыльную пленку ( 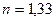), интерференционная картина изменилась на противоположную. При какой наименьшей толщине 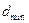пленки это возможно?

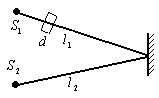Решение. Изменение интерференционный картины на противоположную означает, что на тех участках экрана, где наблюдались интерференционные максимумы, стали наблюдаться интерференционные минимумы. Такой сдвиг интерференционный картины возможен при изменении оптической разности хода пучков световых волн на нечетное число половин длин волн т.е.

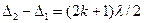, (1) где 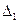– оптическая разность хода пучков до внесения пленки, 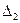– оптическая разность хода тех же пучков после внесения пленки,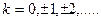

Наименьшей толщине 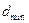пленки соответствует 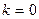. При этом формула (1) примет вид : 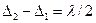. (2)

Вычислим оптические разности хода 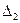и 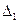. Из рисунка следует 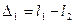, 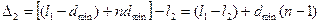. Подставим выражения 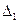и 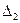в формулу (2): 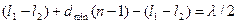, или 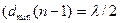. Отсюда .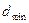

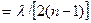Произведем вычисления: .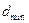

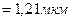Пример10.На дифракционную решетку в направлении нормали к ее поверхности падает монохроматический свет. Период решетки 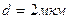. Определить наибольший порядок дифракционного максимума, который дает эта решетка в случае красного ( 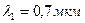) и в случае фиолетового ( 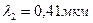) света.

Решение. Из формулы определяющий положение главных максимумов дифракционной решетки, найдем порядок 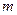дифракционного максимума: 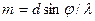, (1)

где 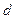– период решетки, 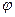–угол дифракции, 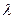– длина волны монохроматического света.. так как 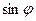не может быть больше 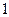, то число 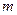не может быть больше 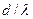, т.е. 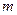≤ 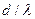. ( 2)

Подставив в формулу (2) значения, получим:

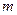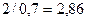≤ (для красных лучей),

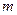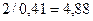≤ (для фиолетовых лучей).

Если учесть, что порядок максимумов является целым числом, то для красного света 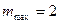и для фиолетового .

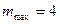Пример 11. Пучок естественного света падает на поляризованную поверхность стеклянной пластины, погруженную в жидкость. Отраженный от пластины пучок света образует угол 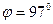с падающим пучком (см. рис.). Определить показатель преломления 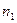жидкости, если отраженный свет максимально поляризован.

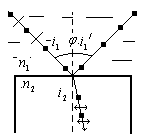Решение. Согласно закону Брюстера пучок света, отраженный от диэлектрика, максимально поляризован в том случае. Если тангенс угла падения численно равен относительному показателю преломления 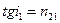, где 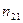показатель преломления второй среды (стекла) относительно первой (жидкости).

Относительный показатель преломления равен отношению абсолютных показателей преломления. Следовательно, 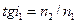и. следовательно, 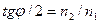, откуда : .

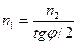Произведя вычисления, находим .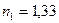

Пример 12.Плоскополяризованный монохроматический пучок света падает на поляроид и полностью им гасится. Когда на пути пучка поместили кварцевую пластинку, интенсивность I пучка света после поляроида стала равна половине интенсивности пучка , падающего на поляроид. Определить минимальную толщину кварцевой пластины. Поглощением и отражением света поляроидом пренебречь, постоянную вращения а кварца принять равной 48,9 град/мм .

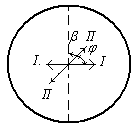Решение.Полное гашение света поляроидом означает, что плоскость пропускания поляроида (пунктирная линия на рисунке) перпендикулярна плоскости колебаний ( 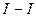) плоскополяризованного света, падающего на него. Введение кварцевой пластины приводит к повороту плоскости колебаний света на угол 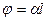, где 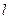– толщина пластины. . (1)

Зная во сколько раз уменьшится интенсивность света при прохождении его через поляроид. Определим угол 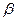, который установится между плоскостью пропускания и новым направлением 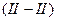плоскости колебаний падающего на поляроид плоскополяризованного света. Для этого воспользуемся законом Малюса: .

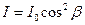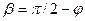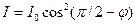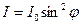Заметив, что , можно написать , или . (2)

Из равенства (2)с учетом (1) получим 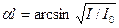. Откуда искомая толщина пластины .

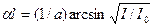Пример 13.Длина волны , на которую приходится максимум энергии в спектре излучения абсолютно черного тела, 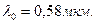Определить энергетическую светимость (излучательность ) 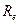поверхности тела.

Решение. Энергетическая светимость 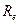абсолютно черного тела в соответствии с законом Стефана–Больцмана пропорциональна четвертой степени термодинамической температуры и выражается формулой: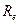 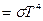, (1) где 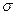– постоянная Стефана–Больцмана, Т– термодинамическая температура.

Температуру Т можно выразить с помощью закона смещения Вина: 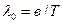, (2)

где 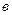– постоянная закона смещения Вина.

Используя формулы (2) и (1), получаем: 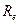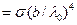. (3)

Произведя вычисления, находим: = .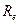

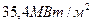Пример 14. В результате Эффекта Комптона фотон при соударении с электроном был рассеян на угол 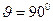. Энергия рассеянного фотона 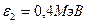. Определить энергию фотона 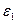до рассеяния.

Решение.Для определения энергии первичного фотона воспользуемся формулой Комптона:

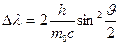, (1)

где 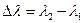– изменение длины волны фотона в результате рассеяния на свободном электроне, h– постоянная Планка , 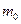– масса покоя электрона, с– скорость света в вакууме, 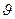– угол рассеяния фотона.

Преобразуем формулу (1): 1) заменим в ней 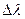на 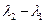, 2) выразим длины волн и 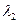через энерги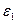и и 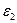соответствующих фотонов, воспользовавшись формулой 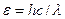, 3) умножим числитель и знаменатель правой части формулы на с . Тогда:

.

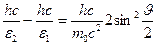Сократим на 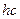и выразим из этой формулы искомую энергию:

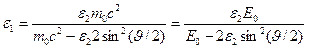, (2)

где 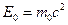– энергия покоя электрона.

Вычисления по формуле (2) удобнее вести во внесистемных единицах. Так как для электрона 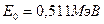, то 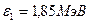.