Задачи для контрольных работ 7 страница

6.37Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределенность радиуса электронной орбиты и неопределенность импульса р электрона на такой орбите соответственно связаны следующим образом: и . Используя эти связи, а также соотношение неопределенностей, найти значение радиуса электронной орбиты, соответствующего минимальной энергии электрона в атоме водорода.

6.38Моноэнергетический пучок электронов высвечивает в центре экрана электронно-лучевой трубки пятно радиусом см. Пользуясь соотношением неопределенностей, найти, во сколько раз неопределенность координаты электрона на экране в направлении, перпендикулярном оси трубки, меньше размера r пятна. Длину L электронно-лучевой трубки принять равной 0,50 м, а ускоряющее электрон напряжение U - равным 20 кВ.

6.39Среднее время жизни Dt атома в возбужденном состоянии составляет около с. При переходе атома в нормальное состояние испускается фотон, средняя длина волны <l> которого равна 400 нм. Оценить относительную ширину излучаемой спектральной линии, если не происходит уширения линии за счет других процессов.

6.40Для приближенной оценки минимальной энергии электрона в атоме водорода можно предположить, что неопределенность радиуса электронной орбиты и неопределенность импульса р электрона на такой орбите соответственно связаны следующим образом: и . Используя эти связи, а также соотношение неопределенностей, определить минимальное значение энергии E_min электрона в атоме водорода.

6.41Определить относительную неопределенность импульса движущейся частицы, если допустить, что неопределенность ее координаты равна длине волны де Бройля.

6.42Электрон движется в атоме водорода по первой боровской орбите. Принимая, что допускаемая неопределенность скорости составляет 10% от ее числового значения, определить неопределенность координаты электрона.

6.43Электронный пучок выходит из электронной пушки под действием разности потенциалов U = 200 В. Определить, можно ли одновременно измерить траекторию электрона с точностью до 100 пм и его скорость с точностью до 10%.

6.44Определить отношение неопределенностей скорости электрона, если его координата установлена с точностью до 10^–5 м, и пылинки массой 10^–12 кг, если ее координата установлена с такой же точностью.

6.45Ширина следа электрона (обладающего кинетической энергией 1,5 эВ) на фотопластинке, полученного с помощью камеры Вильсона, составляет 1 мкм. Определить, можно ли по данному следу обнаружить отклонение в движении электрона от законов классической механики.

6.46Частица находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике. Найти отношение разности соседних энергетических уровней к энергии частицы в трех случаях: 1) ; 2) ; 3) .

6.47Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l = 0,1 нм. Определить в электрон-вольтах наименьшую разность энергетических уровней электрона.

6.48Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l находится в возбужденном состоянии ( ). Определить, в каких точках интервала плотность вероятности нахождения частицы имеет максимальное и минимальное значения.

6.49В прямоугольной потенциальной яме шириной l с абсолютно непроницаемыми стенками ( ) находится частица в основном состоянии. Найти вероятность местонахождения этой частицы в области .

6.50Частица в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения частицы в крайней четверти ящика?

6.51Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид , где А – некоторая постоянная; – первый боровский радиус. Найти для основного состояния атома водорода наиболее вероятное расстояние электрона от ядра.

6.52Частица находится в основном состоянии в прямоугольной яме шириной l с абсолютно непроницаемыми стенками. Во сколько раз отличаются вероятности местонахождения частицы: - в крайней трети и - в крайней четверти ящика?

6.53Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид , где А – некоторая постоянная; - первый боровский радиус. Найти для основного состояния атома водорода среднее значение кулоновской силы.

6.54Электрон находится в бесконечно глубоком, одномерном, прямоугольном потенциальном ящике шириной l. В каких точках в интервале плотности вероятности нахождения электрона на втором и третьем энергетических уровнях одинаковы? Вычислить плотность вероятности для этих точек. Решение пояснить графиком.

6.55Волновая функция, описывающая движение электрона в основном состоянии атома водорода, имеет вид , где А – некоторая постоянная; - первый боровский радиус. Найти для основного состояния атома водорода среднее значение <П> потенциальной энергии.

6.56Электрон находится в прямоугольном потенциальном ящике с непроницаемыми стенками. Ширина ящика l = 0,2 нм, энергия электрона в ящике E = 37,8 эВ. Определить n номер энергетического уровня.

6.57Частица в одномерном прямоугольном потенциальном ящике шириной l с бесконечно высокими стенками находится в возбужденном состоянии (n =3)/ Определить, в каких точках ящика (0 £ x £ l) плотность вероятности обнаружения частицы максимальна. Поясните графически.

6.58Частица в одномерном прямоугольном потенциальном ящике шириной l с бесконечно высокими стенками находится в возбужденном состоянии (n =3)/ Определить, в каких точках ящика (0 £ x £ l) плотность вероятности обнаружения частицы минимальна. Поясните графически.

6.59Математический маятник можно рассматривать в качестве гармонического осциллятора. Определите в электрон-вольтах энергию нулевых колебаний для маятника длиной l = 1 м, находящегося в поле тяготения Земли.

6.60Частица в потенциальном ящике находится в основном состоянии. Какова вероятность обнаружения частицы в средней трети ящика?

7.1Найти период полураспада радиоактивного изотопа, если его активность за время сут уменьшилась на 24% по сравнению с первоначальной.

7.2Определить, какая доля радиоактивного изотопа распадается в течение времени t = 6 сут.

7.3Активность А некоторого изотопа за время t = 10 сут уменьшилась на 20%. Определить период полураспада этого изотопа.

7.4Определить массу m изотопа , имеющего активность А = 37 ГБк.

7.5Найти среднюю продолжительность жизни атома радиоактивного изотопа кобальта .

7.6Счетчик -частиц, установленный вблизи радиоактивного изотопа, при первом измерении регистрировал N₁ = 1400 частиц в минуту, а через время t = 4 ч - только N₂ = 400. Определить период полураспада изотопа.

7.7Во сколько раз уменьшится активность изотопа через время t = 20 сут?

7.8На сколько процентов уменьшится активность изотопа иридия за время сут?

7.9Определить число N ядер, распадающихся в течение времени: 1) мин; 2) сут, - в радиоактивном изотопе фосфора массой мг.

7.10Из каждого миллиона атомов радиоактивного изотопа каждую секунду распадается 200 атомов. Определить период полураспада изотопа.

7.11Изотоп радия с массовым числом 226 превратился в изотоп свинца с массовым числом 206. сколько a- и b-распадов произошло при этом?

7.12Может ли ядро кремния превратиться в ядро фосфора? Какие частицы должны при этом выделиться? Какова их суммарная энергия?

7.13Активность препарата урана с массовым числом 238 равна 2,5×10⁴ расп/с, масса препарата 2 г. Найти период полураспада.

7.14Определить во сколько раз начальное количество ядер радиоактивного изотопа уменьшится за три года, если за один год оно уменьшилось в 4 раза.

7.15Активность некоторого радиоактивного изотопа в начальный момент времени составляла 100 Бк. Определите активность этого изотопа по истечении промежутка времени, равного половине периода полураспада.

7.16Определить количество теплоты Q, выделяющейся при распаде радона активностью Бк за время t = 20 мин. Кинетическая энергия Т вылетающей из радона -частицы равна 5,5 МэВ.

7.17Масса г урана в равновесии с продуктами его распада выделяет мощность Вт. Найти молярную теплоту , выделяемую ураном за среднее время жизни атомов урана.

7.18Определить энергию, необходимую для разделения ядра на две -частицы и ядро . Энергии связи на один нуклон в ядрах ²⁰Ne, ⁴He и ¹²С равны соответственно 8,03; 7,07 и 7,68 МэВ.

7.19В одном акте деления ядра урана освобождается энергия 200 МэВ. Определить: 1) энергию, выделяющуюся при распаде всех ядер этого изотопа урана массой кг; 2) массу каменного угля с удельной теплотой сгорания q = 29,3 МДж/кг, эквивалентную в тепловом отношении 1 кг урана .

7.20Мощность Р двигателя атомного судна составляет 15 МВт, его КПД равен 30%. Определить месячный расход ядерного горючего при работе этого двигателя.

7.21Считая, что в одном акте деления ядра урана освобождается энергия 200 МэВ, определить массу т этого изотопа, подвергшегося делению при взрыве атомной бомбы с тротиловым эквивалентом кг, если тепловой эквивалент тротила q равен 4,19 МДж/кг.

7.22При делении ядра урана под действием замедленного нейтрона образовались осколки с массовыми числами и . Определить число нейтронов, вылетевших из ядра в данном акте деления. Определить энергию и скорость каждого из осколков, если они разлетаются в противоположные стороны и их суммарная кинетическая энергия Т равна 160 МэВ.

7.23Ядерная реакция вызвана -частицей, обладавшей кинетической энергией МэВ. Определить тепловой эффект этой реакции, если протон, вылетевший под углом = 60° к направлению движения a-частицы, получил кинетическую энергию МэВ.

7.24Определить тепловые эффекты следующих реакций:

и

7.25Определить скорости продуктов реакции , протекающей в результате взаимодействия тепловых нейтронов с покоящимися ядрами бора.

7.26Ядро урана ²³⁵U при делении освобождает энергию 200 МэВ. При взрыве урановой бомбы успевает прореагировать около 1,5 кг урана. Какова масса эквивалентной тротиловой бомбы, если теплотворная способность тротила 4,1 МДж/кг?

7.27Какую минимальную кинетическую энергию должна иметь a-частица для осуществления ядерной реакции ?

7.28Найти минимальную кинетическую энергию протона, способного "разбить" ядро дейтерия на протон и нейтрон.

7.29Атомная электростанция мощностью P = 1000 Вт имеет КПД 20%. Какова масса m расходуемого за сутки урана-235? Считать, что при каждом делении ядра урана выделяется энергия W₀ = 200 МэВ.

7.30Сколько железнодорожных вагонов массой M = 60 т каждый можно было бы поднять на высоту h = 1 км за счет энергии, вырабатываемой АЭС (см. предыдущую задачу) за сутки? На какую величину Dm уменьшается при этом масса ядерного горючего?

7.31Возможен ли следующий процесс: ? Объяснить.

7.32Возможен ли следующий процесс: ? Объяснить.

7.33Возможен ли следующий процесс: ? Объяснить.

7.34Возможен ли следующий процесс: ? Объяснить.

7.35Возможен ли следующий процесс: ? Объяснить.

7.36Возможен ли следующий процесс: ? Объяснить.

7.37Возможен ли следующий процесс: ? Объяснить.

7.38Возможен ли следующий процесс: ? Объяснить.

7.39Возможен ли следующий процесс: ? Объяснить.

7.40Возможен ли следующий процесс: ? Объяснить.

7.41Возможен ли следующий процесс: ? Объяснить.

7.42Возможен ли следующий процесс: ? Объяснить.

7.43Возможен ли следующий процесс: ? Объяснить.

7.44Используя информацию о квантовых числах кварков, сконструировать из трех кварков следующие барионы: p, n, S ⁺. Ответ пояснить.

7.45Используя информацию о квантовых числах кварков, сконструировать из кварка и антикварка следующие мезоны: p ⁺, p ^–, K⁰. Ответ пояснить.

7.46Мезон космических лучей имеет энергию W = 3 ГэВ. Энергия покоя мезона W₀ = 100 МэВ. Какое расстояние l в атмосфере сможет пройти мезон за время его жизни t по лабораторным часам? Собственное время жизни мезона t₀ = 2 мкс.

7.47Мезон космических лучей имеет кинетическую энергию W = 7m₀c², где m₀ – масса покоя мезона. Во сколько раз собственное время жизни t₀ мезона меньше времени его жизни t по лабораторным часам?

7.48Электрон и позитрон образуются фотоном с энергией 2,26 МэВ. Какова была в момент возникновения полная кинетическая энергия позитрона и фотона?

7.49Неподвижный K⁰-мезон распадается на два заряженных p-мезона. Масса покоя K⁰-мезона m₀(K⁰)=965m₀, где m₀ – масса покоя электрона. Масса каждого p-мезона m(p) = 1,77m₀(p), где m₀(p) – его масса покоя. Найти массу покоя p-мезонов.

7.50Максимальный радиус кривизны траектории частиц в циклотроне R = 50 см, а магнитная индукция поля B = 1 Тл. Какую постоянную разность потенциалов должны пройти протоны, чтобы получить такое же ускорение, как в данном циклотроне?

7.51В фазотроне увеличение массы частицы при возрастании ее скорости компенсируется увеличением периода ускоряющего поля. Частота разности потенциалов, подаваемой на дуанты фазотрона, менялась для каждого ускоряющего цикла от n₀ = 25 МГ до n = 18,9 МГ. Найти магнитную индукцию поля фазотрона и кинетическую энергию вылетающих протонов.

7.52При упругом центральном столкновении нейтрона с неподвижным ядром замедляющего вещества кинетическая энергия нейтрона уменьшилась в 1,4 раза. Найти массу ядер замедляющего вещества.

7.53Электрон ускорен разностью потенциалов U = 180 кВ. Учитывая поправки теории относительности, найти для этого электрона массу m.

7.54До какой энергии E можно ускорить a-частицы в циклотроне, если относительное увеличение массы частицы не должно превышать 5%?

7.55Энергия дейтронов, ускоренных синхротроном, W = 200 МэВ. Найти скорость дейтронов. (масса покоя дейтрона m₀ = 3,35×10^–27 кг)

7.56Для получения медленных нейтронов их пропускают через вещества, содержащие водород, например, парафин. Какую наибольшую часть своей кинетической энергии нейтрон массой m₀ может предать протону (масса m₀).? Наибольшая часть передаваемой энергии соответствует упругому центральному столкновению.

7.57Позитрон и электрон аннигилируют, образуя два фотона. Найти длину волны каждого из фотонов, считая, что начальная энергия частиц ничтожна мала.

7.58Нейтрон и антинейтрон аннигилируют, образуя два фотона. Найти частоту каждого из фотонов, считая, что начальная энергия частиц ничтожно мала.

7.59Заряженная частица влетает в однородное магнитное поле с индукцией B = 0,5 Тл и движется по окружности с радиусом R = 10 см. Скорость частицы v = 2,4×10⁶ м/с. Найти для этой частицы отношение ее заряда к массе.

7.60Поток заряженных частиц влетает в однородное магнитное поле с индукцией B = 3 Тл. Скорость частиц v = 1,52×10⁷ м/с и направлена перпендикулярно к направлению поля. Найти заряд каждой частицы, если известно, что на нее действует сила F = 1,46×10^–11 Н.

8.1Собственная угловая частота w колебаний молекулы HCl равна 5,63×10¹⁴ с^–1, коэффициент ангармоничности g = 0,0201. Определить энергию DE_2,1 (в электрон-вольтах) перехода молекулы с первого на второй колебательный энергетический уровень.

8.2См. условие задачи 8.1. Определить максимальное квантовое число n_max.

8.3См. условие задачи 8.1. Определить максимальную колебательную энергию E_max (в электрон-вольтах).

8.4См. условие задачи 8.1. Определить энергию диссоциации E_d (в электрон-вольтах).

8.5Собственная круговая частота w колебаний молекулы CO равна 4,08×10¹⁴ с^–1,. Определить коэффициент b квазиупругой силы.

8.6Определить число колебательных энергетических уровней, которое имеет молекула HBr, если коэффициент ангармоничности g = 0,0208.

8.7Собственная круговая частота w колебаний молекулы O₂ равна 2,98×10¹⁴ с^–1, коэффициент ангармоничности g = 9,46×1^–3. Определить максимальную колебательную энергию E_max (в электрон-вольтах) молекулы.

8.8Для молекулы HF определить момент инерции. Межъядерное расстояние d = 91,7 пм.

8.9Для молекулы HF определить вращательную постоянную B (в электрон-вольтах). Межъядерное расстояние d = 91,7 пм.

8.10Для молекулы HF определить энергию (в электрон-вольтах), необходимую для возбуждения молекулы на первый вращательный уровень. Межъядерное расстояние d = 91,7 пм.

8.11Определить момент импульса L молекулы кислорода, вращательная энергия которой равна 2,16 эВ.

8.12Определить момент инерции J межъядерное расстояние d молекулы CO, если интервалы DE между соседними линиями чисто вращательного спектра испускания молекулы CO равны 0,48 эВ.

8.13Определить для молекулы HCl вращательные квантовые числа Á двух соседних уровней, разность энергий DE_Á+1,_Á которых равна 7,86 эВ.

8.14Для молекулы NO определить температуру T, при которой средняя кинетическая энергия поступательного движения молекулы равна энергии необходимой для ее возбуждения на первый вращательный энергетический уровень. Вращательная постоянная 0,212 эВ.

8.15Найти момент L импульса двухатомной молекулы, соответствующий низшему энергетическому состоянию.

8.16Определить теплоту Q, необходимую для нагревания кристалла калия массой m = 200 г от температуры T₁ = 4 К до температуры T₂ = 5 К. Принять характеристическую температуру Дебая для калия Q_E = 100 К и считать условие 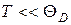о выполненным.

8.17Вычислить характеристическую температуру 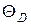Дебая для железа, если при температуре Т = 20 К молярная теплоемкость железа Дж/К·моль. Условие 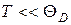считать выполненным.