Энтропия дискретного ансамбля сообщений
Среднее количество информации, содержащееся в ансамбле 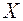 , определяется математическим ожиданием
, определяется математическим ожиданием
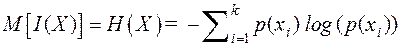 . (2.6)
. (2.6)
Величина 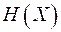 называется энтропией ансамбля
называется энтропией ансамбля 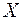 и имеет размерность
и имеет размерность 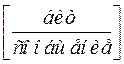 . Под термином сообщение понимается элемент ансамбля
. Под термином сообщение понимается элемент ансамбля 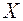 : это может быть символ или набор символов, образующих некоторое сообщение и т. д.
: это может быть символ или набор символов, образующих некоторое сообщение и т. д.
Пример 1.Положим, 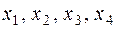 образуют ансамбль сообщений
образуют ансамбль сообщений 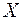 . Вероятности реализаций этих сообщений соответственно равны
. Вероятности реализаций этих сообщений соответственно равны 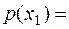 0.1,
0.1, 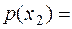 0.4,
0.4, 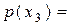 0.2,
0.2, 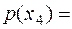 0.3. Определим количество информации, содержащуюся в каждом сообщении, и меру неопределённости в ансамбле
0.3. Определим количество информации, содержащуюся в каждом сообщении, и меру неопределённости в ансамбле 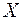 .
.
После расчетов получим
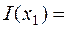 3.3219
3.3219 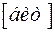 ,
, 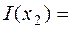 1.3219
1.3219 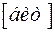 ,
, 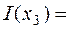 2.3219
2.3219 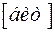 ,
, 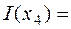 1.7369
1.7369 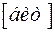 .
.
Энтропия ансамбля равна 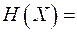 1.84644
1.84644 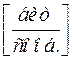 .
.
Как видно, наибольшее количество информации содержится в сообщении 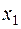 , которая реализуется с наименьшей вероятностью, и наименьшее количество информации содержится в сообщении
, которая реализуется с наименьшей вероятностью, и наименьшее количество информации содержится в сообщении 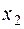 , вероятность реализации которой наибольшая. Чем ближе к единице вероятность реализации сообщения, тем меньше информации содержится в этом сообщении. Эти выводы хорошо согласуются с субъективным представлением о ценности получаемых сведений.
, вероятность реализации которой наибольшая. Чем ближе к единице вероятность реализации сообщения, тем меньше информации содержится в этом сообщении. Эти выводы хорошо согласуются с субъективным представлением о ценности получаемых сведений.
Пример 2. Положим, одно из сообщений ансамбля 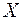 реализуется с вероятностью
реализуется с вероятностью 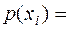 0. Тогда какое-то другое сообщение будет реализовываться с вероятностью
0. Тогда какое-то другое сообщение будет реализовываться с вероятностью 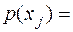 1. Вычислим энтропию вновь полученного ансамбля
1. Вычислим энтропию вновь полученного ансамбля 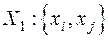 .
.
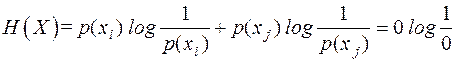 .
.
Получили неопределённость типа 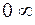 . Разрешив эту неопределённость, получим
. Разрешив эту неопределённость, получим 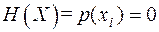 . Неопределённость в ансамбле
. Неопределённость в ансамбле 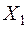 отсутствует.
отсутствует.
Энтропия 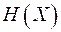 характеризует меру средней неопределённости ансамбля
характеризует меру средней неопределённости ансамбля 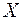 .Пусть задан ансамбль
.Пусть задан ансамбль 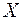 : {
: { 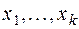 } с распределением вероятностей
} с распределением вероятностей 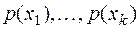 ,
, 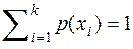 . Тогда энтропия
. Тогда энтропия 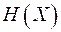 удовлетворяет неравенству
удовлетворяет неравенству
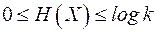 . (2.7)
. (2.7)
 Доказательство. Левая часть неравенства следует из определения энтропии ансамбля
Доказательство. Левая часть неравенства следует из определения энтропии ансамбля 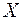 . Для доказательства правой части рассмотрим разность
. Для доказательства правой части рассмотрим разность 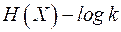 и преобразуем её
и преобразуем её
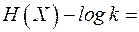
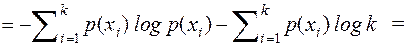
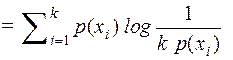
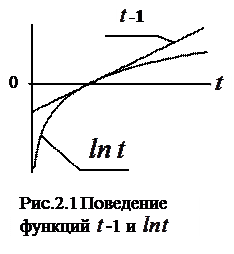
В дальнейшем используем неравенство 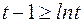 , рисунок 2.1. Знак равенства будет только в случае
, рисунок 2.1. Знак равенства будет только в случае 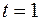 . Тогда имеем
. Тогда имеем
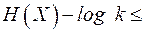
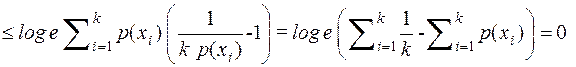 .
.
Из последнего неравенства следует, что знак равенства в правой части неравенстве (2.7) будет в том случае, если
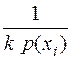 = 1 или
= 1 или 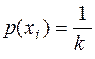 .
.
Энтропия 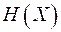 ансамбля
ансамбля 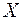 будет максимальной, если все события
будет максимальной, если все события 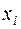 равновероятны. Ценность информации в каждом
равновероятны. Ценность информации в каждом 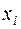 сообщении, с точки зрения частоты её появления в результате опытов, будет равна
сообщении, с точки зрения частоты её появления в результате опытов, будет равна 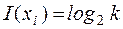 .
.
Вычислим энтропию произведения ансамблей 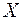 :
: 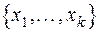 и
и 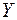 :
: 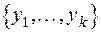 . Произведение ансамблей образует матрицу сообщений
. Произведение ансамблей образует матрицу сообщений
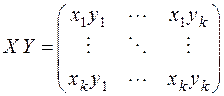
с распределением вероятностей
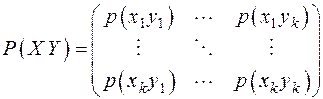 .
.
Пользуясь определением энтропии ансамбля, запишем энтропию произведения ансамблей
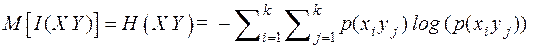 =
=
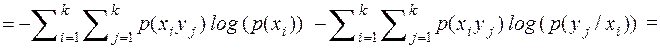
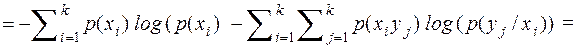
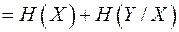
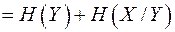 (2.8)
(2.8)
Условная энтропия 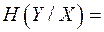
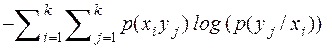 зависит от условной меры информации
зависит от условной меры информации 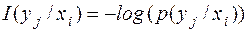 - количества информации, содержащаяся в сообщении
- количества информации, содержащаяся в сообщении 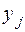 , при условии, что уже реализовалось сообщение
, при условии, что уже реализовалось сообщение 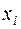 , т.е.
, т.е. 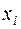 - это не случайное событие в условной мере информации
- это не случайное событие в условной мере информации 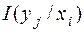 , случайность реализации
, случайность реализации 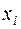 учитывается в вероятности
учитывается в вероятности 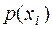 .
.
Если ансамбли 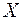 и
и 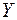 независимы, т.е.
независимы, т.е. 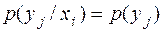 , то энтропия произведения ансамблей равна сумме энтропий ансамблей
, то энтропия произведения ансамблей равна сумме энтропий ансамблей 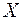 и
и 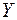
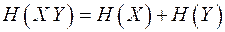 . (2.9)
. (2.9)
Пользуясь методикой, применяемой при доказательстве неравенства (2.6), можно показать, что
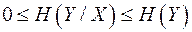 . (2.10)
. (2.10)
Если имеется множество ансамблей 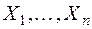 , то энтропия произведения ансамблей равна
, то энтропия произведения ансамблей равна
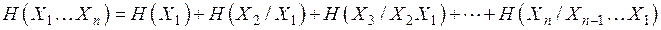 ,
,
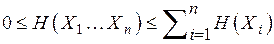 (2.11)
(2.11)
