Формула (10) набуде такого вигляду

Лабораторна робота №5-9

З дисципліни: «Фізика»

На тему: «Визначення сталої Стефана – Больцмана»

Підготував: студент групи МІТ-11(б)

Сікорський Дмитро

Перевірили: к.ф.-м.н.,доц. Стасенко В.А.

пров.інж. Камінський О.С.

Вінниця 2012

Мета роботи:вивчити закони теплового випромінювання абсолютно чорного тіла, визначити сталу Стефана-Больцмана.

Прилади і матеріали:термоелектричний пірометр, автотрансформатор, амперметр, вольтметр, лампа розжарювання.

Теоретичні відомості

Випромінювання, причиною якого є збудження атомів і молекул внаслідок їх теплового руху, називається тепловим або температурним випромінюванням.

Теплове випромінювання характеризується енергетичною світністю або інтегральною випромінювальною здатністю R_e тіла і спектральною густиною енергетичної світності r(v, Т).

Енергетичною світністю R_e тіла називається величина, яка дорівнює потужності випромінювання з одиниці площі поверхні тіла в усьому інтервалі частот хвиль і в усіх напрямах випромінювання:

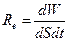, (1)

де W - енергія випромінювання;

S – площа тіла;

t – час.

Розподіл енергії в спектрі випромінювання описується спектральною густиною енергетичної світності r(v,T). Спектральна густина енергетичної світності вимірюється потужністю, випромінюваною з одиниці площі поверхні тіла в інтервалі частот (v,v+dv):

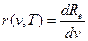. (2)

Нехай з усієї падаючої на тіло енергії dW монохроматичного світла в інтервалі частот (v,v+dv) енергія dW₁ поглинається, а енергія dW₂ відбивається, тоді величину

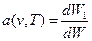, (3)

називають коефіцієнтом монохроматичного поглинання або спектральною поглинальною здатністю тіла.

Тіло, для якого поглинальна здатність дорівнює одиниці, називається абсолютно чорним тілом. Це поняття є ідеалізацією. У природі відсутні тіла, властивості яких збігалися б з властивостями абсолютно чорних тіл. До таких тіл наближаються сажа і дрібнодисперсний порошок платини.

Розглянемо замкнуту систему тіл, яка не має теплообміну з навколишнім середовищем. Через деякий час тіла цієї системи перейдуть у стан рівноваги, тобто відбудеться вирівнювання температур всіх тіл системи. Але це не означає, що теплове випромінювання всередині системи припиниться. Якщо система досягла стану рівноваги, то в будь-який момент часу випромінювана енергія дорівнює поглинутій.

Г.Кірхгоф, виходячи з другого принципу термодинаміки, встановив, що відношення спектральної густини енергетичної світності до спектральної поглинальної здатності є сталою величиною для всіх тіл, для вузького діапазону частот випромінювання при даній температурі:

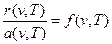. (4)

Це твердження є формулюванням закону Кірхгофа для теплового випромінювання. З цього закону можна зробити висновок, що тіло, яке поглинає промені деяких частот, буде їх же випромінювати і навпаки.

З співвідношення (4) видно, що функція f(v,T) є універсальною. Вона не залежить від природи тіл і є функцією тільки частоти хвиль і температури. Оскільки для абсолютно чорного тіла a(v,T) = 1, то r(v,T)=f(v,T), тобто f(v,T) є спектральною густиною енергетичної світності абсолютно чорного тіла.

Явний вираз функції f(v,T) одержав М. Планк в 1900 р. Виходячи з гіпотези про квантову природу випромінювання методами статистичної фізики він довів, що

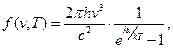(5)

де h - стала Планка;

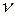– частота коливань;

с - швидкість світла у вакуумі;

k - стала Больцмана;

Т - термодинамічна температура.

Практичні дослідження привели до відкриття трьох загальних законів випромінювання абсолютно чорного тіла. Перший з цих законів називається законом Стефана-Больцмана: енергетична світність абсолютно чорного тіла пропорційна четвертому степеню термодинамічної температури:

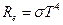, (6)

де σ - стала Стефана-Больцмана.

Якщо середовище, яке оточує абсолютно чорне тіло, має деяку температуру T_С,то воно випромінює енергію, яку частково поглинає абсолютно чорне тіло. Припускаючи, що середовище також є абсолютно чорним тілом, то результуючу енергетичну світність абсолютно чорного тіла можна визначати за формулою:

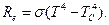(7)

Другий закон теплового випромінювання (закон зміщення Віна) стверджує, що довжина світлової хвилі, на яку припадає максимум спектральної густини енергетичної світності, обернено пропорційна термодинамічній температурі:

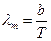, (8)

де b - стала закону зміщення Віна.

Відповідно до цього закону, чим вища температура абсолютно чорного тіла, там на більш коротку хвилю припадає максимум його спектральної густини енергетичної світності (рис. 1).

Третій закон теплового випромінювання стверджує, що максимальна спектральна густина енергетичної світності абсолютно чорного тіла зростає пропорційно п'ятому степеню термодинамічної температури:

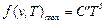, (9)

де С´=1,3 · 10^-5 Вт/м²К².

Після того, як М. Планку вдалось знайти вигляд функції (5), з'явилась можливість теоретичного доведення законів теплового випромінювання.

Закон Стефана-Больцмана можна одержати, використовуючи формулу Планка (5):

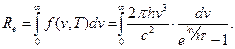(10)

Введемо заміну

.

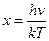Далі знаходимо:

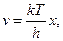
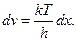
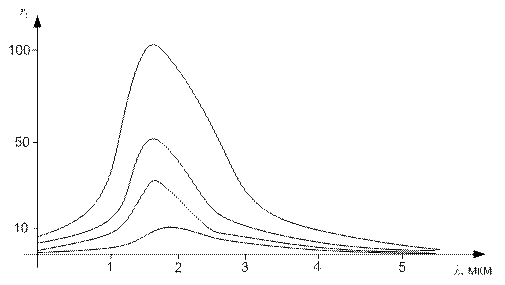
Рис.1

Формула (10) набуде такого вигляду

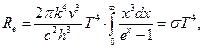(11)

де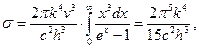

а 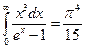– табличний інтеграл.

Закон зміщення Віна зручніше доводиться, якщо записати формулу Планка в такому вигляді:

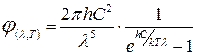. (12)

Для знаходження λ_m потрібно знайти похідну 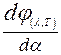і прирівняти її до нуля.

Максимум спектральної густини енергетичної світності знайдемо в результаті підстановки знайденого значення λ_m у формулу (11).

У даній роботі потрібно визначити сталу Стефана-Больцмана шляхом реєстрації випромінювання вольфрамової нитки лампи розжарювання.

Потужність, яка підводиться до випромінювальної поверхні площею S дорівнює:

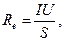(13)

де I – сила струму;

U ­– напруга на нитці розжарення;

S – поверхня випромінювання.

Зіставляючи формули (7) і (13), одержуємо:

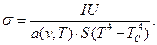(14)

Для вольфраму в інтервалі температур 800 - 1400°С а(v, T) = 0,8.

Радіаційну температуру розжареної вольфрамової нитки в даній роботі визначають за допомогою термоелектричного пірометра. Істинну температуру розжареної вольфрамової нитки визначають за допомогою графіка, який розміщений на установці.

Порядок виконання роботи

1. Ввімкнути автотрансформатор в електричну мережу.

2. Ввімкнути в електричну мережу термоелектричний пірометр.

3. Виміряти силу струму, що протікає в нитці розжарення лампи.

4. Виміряти напругу, прикладену до нитки розжарення.

5. Виміряти радіаційну температуру нитки розжарення за допомогою термоелектричного пірометра.

6. За допомогою графіка визначити істинну температуру.

7. Повторити вимірювання п.п. 3...5 ще при двох значеннях напруги.

8. Всі дані вимірювань занести в таблицю.