Тақырып №22. Тербелмелі қозғалыс.Математикалық маятниктің периодының формуласы.

6.2 Сабақ міндеті:

1.Тербелмелі қозғалыс және математикалық маятник туралы ұғындыру.

2.Білімгерлердің білімін арттыру, тереңдету.

3.Білімгерлерді ұқыптылыққа тәрбиелеу.

6.3 Дәріс тезисі:

Тербеліс деген өте кең ұғым. Айталық маятник тербелісі, машиналар двигателі, поршеннің қозғалысы, кеменің шайқалысы, көпірдің теңселісі, айнымалы токтың тізбектегі тербелісі, жүрек соғысы, жел соққанда талдың тербелісі және «Тербелер даусым ауада...» деп Сәкен Сейфуллин айтқан ауаның тербелісі, «Желсіз түнде жарық ай. Сәулесі суда дірілдеп» дегендей су бетіндегі тербеліс толқындары, осының бәрі тербелістердің мысалдары бола алады.

Тербеліске мысал:ағаш бұтақтары,әткеншек,бесік,домбыра шегі,таразы сілтемесі,қабырға сағатының маятнигі.Бұл қозғалыстардың ұқсастығы:барлығы қайталанып отырады,уақыт өткен соң тербеліп тұрады.

Тербелістер деп дененің бірдей уақыт аралығындағы дәлме-дәл немесе жуықтап қайталанып отыратын қозғалысын айтады.

Тербеліс деп дененің бірдей уақыт аралығында дәлме-дәл немесе жуықтап қайталанып отыратын қозғалысын айтады.

Тербелмелі қозғалыс деп – тепетеңдік күйде тұрған дененің уақыт бірлігінде сол орнынан периодты ауытқуына айтады. Тербелмелі қозғалыс болу үшін тербеліс көзі немесе контуры болуы шарт. Оларға: математикалық маятник, пружиналық маятник, физикалық маятник. Электромагниттік тербелмелі контур ол транзистордан, электр сыйымдылықтан және индуктивтен тұратын жүйені айтады.

Тербелмелі қозғалыс жиілікпен, периодпен сипатталады. Әрқайсысы контурдың өзіне сәйкес жиілігімен периоды болады.

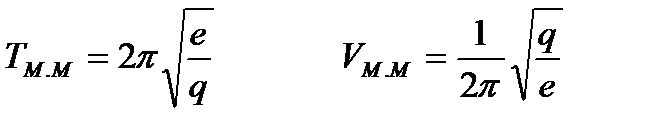- Математикалық маятник.

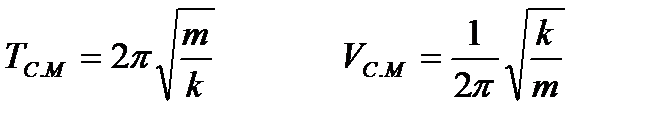- Серіппелі маятник

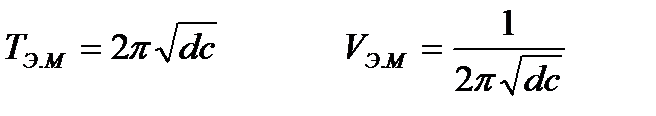- Электромагниттік маятник.

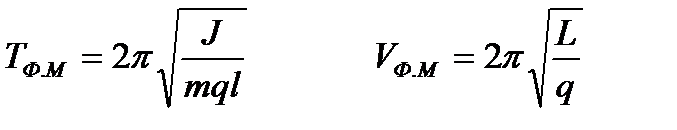- физикалық маятник

Мұндағы J – инерция моменті J=ml², L – дененің асылу нүктесінен тепе – теңдікте тұрғандағы дене ұшының нүктесіне дейінгі қашықтықтығы.

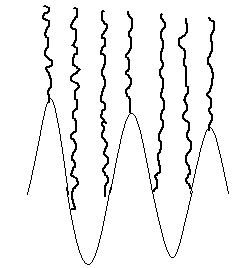
2) Спектр деп – торға түскен тербелістерді немесе толқындарды айтады. Тор дегенде берілген уақыт ескеріледі.

3) Гармониялық спектрлер деп – синусоидалық немесе косинусоидалық заңмен қозғалатын тербелістердің спектіріне айтады. Бұл заң бойынша тербеліп жатқан дененің амплитудасы периоды өзгермес болады.

4) Амплитуда деп тербелістегі дененің тепе – теңдік нүктесінен максимал ауытқуына айтады. Оны А әріпімен белгілейді. 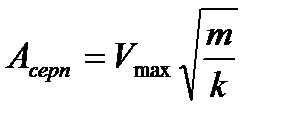Тербеліп жатқан дененің уақыт бойынша көшуі: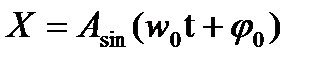 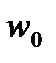- циклдік жиілік, 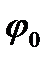- бастапқы фазасы.

Тербеліп жатқан дененің жылдамдығы:

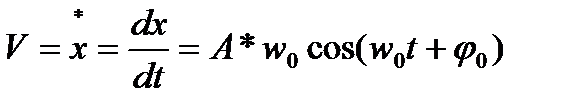
Тербеліп жатқан дененің үдеуі:

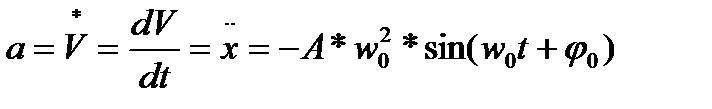
Жылдамдық пен үдеудің бір-бірінен ерекшелігі мен ұқсастығы: Жылдамдық өзгермесе үдеу болмайды, ал ерекшелігі біреу максимум болған жайда екіншісі минимумға айналады, немесе керісінше. Тепетеңдік күйде немесе x=0 – де x₀=0 V_max ал А_min

Максимум ауытқуда: Х_m V=0 ал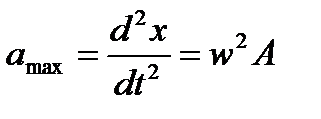

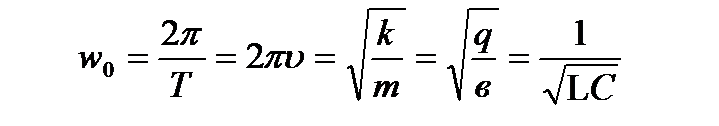
F= -kX F-серпімділік күші

k-серіппе қатаңдығы

Х-серіппе ұзаруы,ығысуы

Ығысуға пропорционал және оған 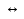бағытталған күштің әрекетінен болатын механикалық тербелістер гармоникалық тербелістер деп аталады.

Тербелмелі процестер жүзеге асатын құрылғыларды тербелмелі жүйелер деп атайды. Осындай жүйелердің қарапайым түрі—математикалық маятниктің тербелісін қарастырайық. Математикалық маятник деп созылмайтын салмақсыз жіңішке ұзын жіпке ілінген кішкентай ауыр шарды айтады.

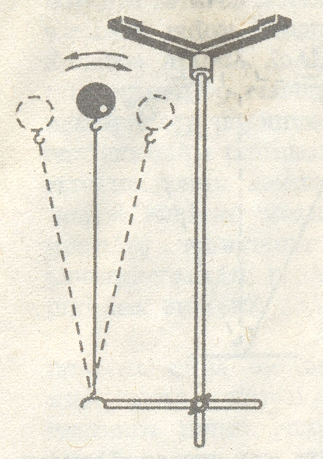
Тербелмелі жүйелерге тән белгілердің бәрі математикалық маятникте де болады. Егер маятникті тепе-теңдік күйінен ауытқытатын болсақ, онда ол әрекет етуші күштерді теңгеруші күштің әрекетінен бастапқы тепе-теңдік күйіне қайта оралады. Осындай маятниктердің қозғалысын бақылап отырып, келесі қарапайым заңдарды тағайындауға болады.

1. Егер маятниктің ұзындығын өзгертпей, оған массалары әр түрлі жүктер ілсек, онда маятниктің тербеліс периодының өзгермейтіндігі байқалады. Демек, математикалық маятниктің периоды жүктің массасына тәуелді болмайды.

2. Егер маятникті қозғалысқа келтіргенде оны әр түрлі бұрышқа ауытқытатын болсақ, онда ол амплитудасы түрліше болғанымен, бірдей периодпен тербеледі. Амплитудасы өте үлкен болмаған жағдайда бұл тербеліс гармоникалық тербеліске мейлінше жуық болады. Математикалық маятниктің периоды тербеліс амплитудасына тәуелді болмайды.

Математикалық маятниктің тербеліс периоды

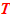=2π