Определить комплексные амплитуды поперечных составляющих вектора , а затем из уравнений Максвелла определить комплексные амплитуды составляющих вектора , используя соотношение
Содержание
1. Техническое задание………………………………………………………………...2
2. Определение комплексных амплитуд составляющих вектора 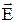 и
и 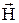 …………..4
…………..4
3. Определение диапазона частот, в котором рассматриваемое поле -
бегущая волна………………………………………………………………………...6
4. Выражения для мгновенных значений всех составляющих векторов 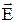 и
и 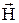 …..6
…..6
5.Расчет и построение графиков зависимостей амплитуд составляющих
векторов поля от координат x, y, z………………………………………………….....8
7. Проверка выполнения граничных условий………………………………………….16
8. Определение комплексных амплитуд плотностей поверхностных
токов и зарядов…………………………………………………………………………16
9. Определение выражений для комплексного вектора Пойнтинга. Среднее за период значение плотности потока энергии. Амплитуда плотности реактивного потока энергии…………………………………………………………………………..20
10. Вычисление среднего за период потока энергии через поперечное сечение трубы…………………………………………………………………………………….22
11. Определение фазовой скорости и скорости распространения энергии.
Расчет и построение графиков их зависимостей от частоты……………………….23
12. Определение коэффициента затухания волны…………………………………..24
13. Расчёт и построение частотной зависимости коэффициента затухания
волны в волноводе……………………………………………………………………..25
14. Определение типа волны, распространяющейся в волноводе, структура силовых линий электрического и магнитного полей этой волны, структура силовых линий плотности поверхностного тока проводимости, протекающего по стенкам волновода……………………………………………………………………………….25
15. Вывод………………………………………………………………………………..29
16. Использованная литература………………………………………………………30
Техническое задание
В полой трубе прямоугольного сечения (Рис. 1) создано монохроматическое электромагнитное поле. Труба заполнена однородной изотропной средой без потерь, абсолютная диэлектрическая и магнитная проницаемости равны 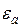 и
и 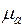 соответственно. Известно, что комплексная амплитуда вектора
соответственно. Известно, что комплексная амплитуда вектора 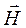 равна:
равна:
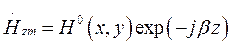 , где
, где 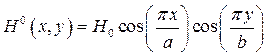 ,
, 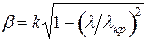 ,
, 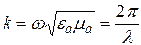 ,
, 
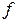 ,
, 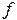 - частота электромагнитных колебаний;
- частота электромагнитных колебаний; 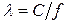 - длина волны, распространяющейся в однородной изотропной непроводящей среде с параметрами
- длина волны, распространяющейся в однородной изотропной непроводящей среде с параметрами 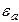 и
и 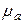 ;
; 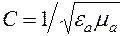 - скорость света в этой среде,
- скорость света в этой среде, 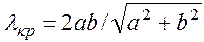 ,
, 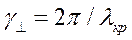
Исходные данные:
| № вар | 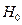 В/м В/м | 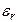 | 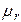 | a см | b см | 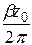 | 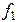 ГГц ГГц | 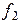 ГГц ГГц |
| 2,25 | 0,75 |
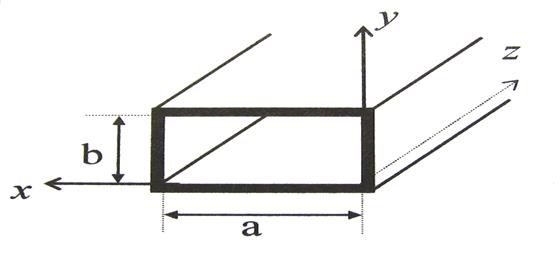

Рис. 1
Параграф № 1
Определить комплексные амплитуды поперечных составляющих вектора , а затем из уравнений Максвелла определить комплексные амплитуды составляющих вектора , используя соотношение
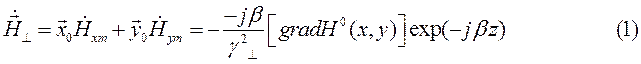 ,
,
Найдем комплексные амплитуды составляющих вектора 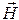 , воспользовавшись вышеприведённым соотношением:
, воспользовавшись вышеприведённым соотношением:
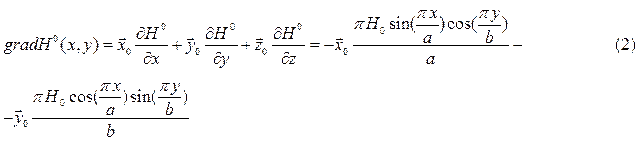
Подставляя значение из (2) в (1) найдём комплексную форму вектора  :
:
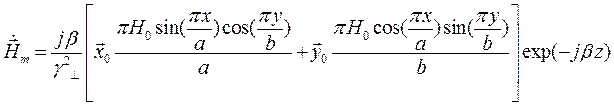
Запишем проекции комплексной амплитуды вектора  на оси координат:
на оси координат:
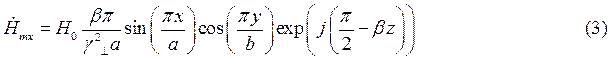
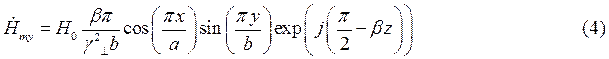
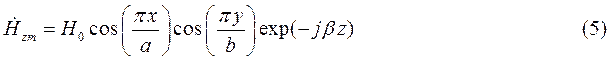
Воспользуемся вторым уравнением Максвелла в комплексной форме для определения комплексной амплитуды вектора 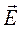 :
:
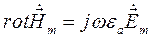 (6)
(6)
Найдем 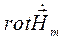 :
:
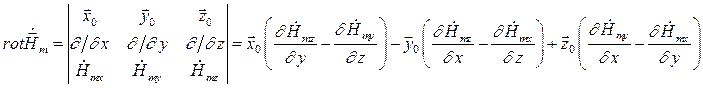
Тогда составляющие комплексной амплитуды вектора 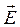 равны соответственно:
равны соответственно:
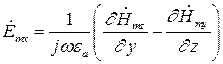 (7)
(7)
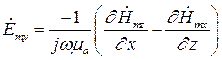 (8)
(8)
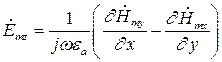
(9)
Найдем выражения для частных производных составляющих комплексной амплитуды вектора 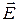 по соответствующим координатам:
по соответствующим координатам:
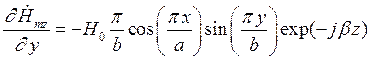
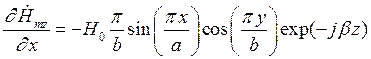
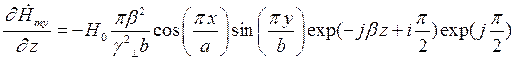
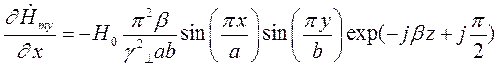
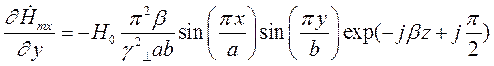
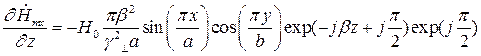
Подставляя найденные значения частных производных в (7), (8) и (9), получим итоговые выражения для комплексных амплитуд составляющих вектора  :
:
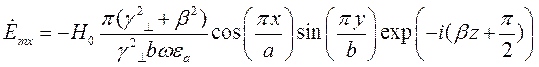 (10)
(10)
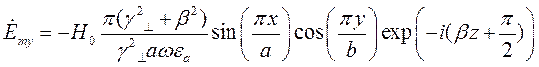 (11)
(11)
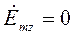 (12)
(12)
Параграф № 2
