Квантовая механика
Квантовая механикавозникла на основе удивительных открытий конца XIX – начала ХХ вв.
Во второй половине XIX века были открыты катодные лучи, которые, как было установлено несколько десятилетий спустя, состоят из электронов. В конце века были открыты рентгеновские Х-лучи и радиоактивность некоторых веществ. Оказалось также, что некоторые вещества, как например уран, испускают лучи, которые не являются катодными. Они получили название α-, β-, и γ-лучей. В начале ХХ в. физики поняли, что эти лучи вылетают из ядер. Было установлено, что первые два вида лучей – это соответственно электроны и ядра гелия, а третий вид – нейтральное сильно проникающее излучение, которое оказались потоком фотонов высоких энергий, или γ-квантов. Открытие фотоэффекта, гипотеза квантов Планка, модели атома Резерфорда и Бора – все это стало базой для создания квантовой теории и более совершенной модели атома. Физики понимали, что электроны внутри ядра двигаются с огромной скоростью и говорить
о каком-либо точном их положении в атоме было бы неверно. Представление об электроне, скачущем с одной орбиты на другую, было слабым приближением к реальности. Нужны были другие подходы к описанию атома.
Накопление огромного экспериментального материала и целый ряд теоретических представлений позволили сделать шаг к созданию новой модели атома. Развитие квантовой теории связано с именами великих физиков XX века – Кюри, Рентгена, Беккереля, Резерфорда, Бора, Планка, Эйнштейна и других. Последней ступенькой к этому стала гипотеза Луи де Бройля и соотношение неопределенности Гейзенберга.
Луи де Бройль39в 1923 году дал обоснование теории Бо-
ра, основываясь на законах симметрии природы. Он предположил, что если фотоны обладают волновыми и корпускулярными свойствами, то и любые другие частицы, например электроны, наряду с корпускулярными обладают и волновыми свойствами. В этом случае частице массой m, движущейся со скоростью v, соответствует длина волны λ, называемая дебройлевской длиной волны:
 l = hmv
l = hmv
, (4.2.1)
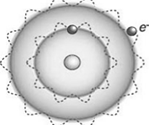
Каждому электрону в атоме, считал де Бройль, соответствует стоячая волна. Хорошо известно, что в пространстве, ограниченном стенками, могут возникнуть лишь стоячие волны, а остальные будут затухать. Такие волны по гипотезе де Бройля могут возникать вдоль орбиты атома, как показано на рис. 4.8, а. В этом случае, возникшие стоячие волны будут замыкаться на себя, т.е. на длине орбиты должно помещаться целое число волн:
2πrn= nλ, n = 1,2,3,… (4.2.2)
Подставляя (4.2.1) в (4.2.2), получаем

39Луи де Бройль (1892–1987) – знаменитый французский физик, член французской Академии наук. Получил образование сначала историка, а затем физика в Парижском университете. В 1929 г. за открытие волновой природы электронов де Бройль был удостоен Нобелевской премии по физике. Член французской Академии наук.
mvrn= nħ.
(4.2.3)
Выражение (4.2.3) представляет собой один из постулатов
Бора или,
как принято его называть, условие квантования.
Спустя несколько лет его гипотеза была подтверждена экспериментально. К.Д. Дэвиссон и Л.Х. Джермер в 1927 г., исследуя рассеяние электронов на поверхности металла, обнаружили дифракционную картину (рис. 4.8, б). Позднее этот же эффект наблюдали для других частиц.
С другой стороны ранее был открыт фотоэффект – рас-
сеяние фотона на связанном (с
атомом)
электроне,
а также
Комптон-эффект –
аналогичное рассеяние фотона
на сво-
бодном (не связанном с атомом) электроне. Объяснить оба эффекта можно в случае, если фотон представляет собой не
волну, а частицу. Это отличается от представлений ческой физики, где свет имеет волновую природу.
класси-

а б
Рис. 4.8. Стоячие волны вдоль орбиты (а)
и дифракция (б) электронов
Анализ недостатков теории Бора при ее огромной значимости для развития физики атома позволил понять, почему в начале 1920-х гг. многие физики стали все более отчетливо
сознавать
необходимость создания новой, более последова-
тельной теории. И менее чем через два года после того, как де Бройль выдвинул гипотезу о волнах материи, Эрвин Шредингер40 и Вернер Гейзенберг41независимо разработали новую, более общую теорию.

40 Эрвин Шредингер (1887–1961) – австрийский физик-теоретик, один из создателей квантовой механики, иностранный почетный член (1934) АН СССР. Он проводил исследования в области кри-
Новая теория, получившая название квантовой механики, создала из корпускулярно-волнового дуализма единую последовательную теорию. Квантовая механика – это теория, устанавливающая способ описания и законы движения микрочастиц, связь величин, описывающих частицы и системы.
Волновая функция.Важнейшими характеристиками любой волны являются ее длина, частота и амплитуда. Для материальных частиц квантовая механика согласно формуле де Бройля (4.2.1) устанавливает соотношение между длиной волны и импульсом частицы p = mv:
|

 ß =
ß =
p mr
. (4.2.4)
В квантовой механике амплитуду, например электронной волны, называют волновой функцией Y. С помощью волновой функции Y описывается положение электрона в атоме.
Интерпретировать волновую функцию Y можно как способ задания в любой точке пространства и в любой момент времени амплитуды «волны материи», подобно тому, как вектор напряженности электрического поля Eзадает амплитуду электромагнитной волны. Однако возможна и другая интерпретация, основанная на корпускулярно-волновом дуализме. Если зависящая от времени и от точки пространства волновая функция Y описывает отдельный электрон (ска-
жем, в атоме), то
Y 2 определяет вероятность найти электрон
в этой точке пространства в выбранный момент времени, т.е. вероятность P нахождения электрона в заданной точке определяется соотношением
P ~ |T|2. (4.2.5)
Для понимания корпускулярно-волнового дуализма воспользуемся данными эксперимента с двумя щелями (рис.4.9). Предположим, что ширина каждой из щелей и расстояние между ними по порядку величины сравнимы с длиной вол-

сталлографии, математической физики, теории относительности, биофизики. В 1933 г. удостоен Нобелевской премии по физике.
41В. Гейзенберг (1901–1976) – немецкий физик. За создание квантовой механики в 1932 г. удостоен Нобелевской премии по физике.
ны, падающей на них. Это справедливо для световой волны или дебройлевской волны электронов. В случае световой волны известно, что на экране позади щелей будет наблюдаться интерференционная картина. Удивительно, что если вместо света взять электроны, то они тоже создадут интерференционную картину. Там, где волновая функция Y обращается в ноль, находится минимум интерференционной картины. Там, где волновая функция Y максимальна, наблюдается максимум интерференционной картины. Таким образом, электрон можно рассматривать как световую волну, движущуюся одновременно через две щели, которая после прохождения щелей интерферирует между собой.
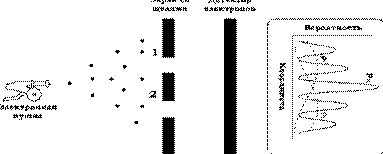
Рис. 4.9. Эксперимент с двумя щелями
Суть всего сказанного сводится к следующему. Если мы трактуем электроны (или какие-либо другие частицы) как волны, то волновая функция Y описывает амплитуду соответствующей материальной волны. Если же мы трактуем электроны как частицы, то Y следует интерпретировать на основе вероятности нахождения электрона в заданной точке.
