Основное уравнение молекулярно-кинетической теории идеальных газов

МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

Молекулярно-кинетическая теория идеальных газов

В физике для описания тепловых явлений используют два основных метода: молекулярно-кинетический (статистический) и термодинамиче­ский.

Молекулярно-кинетический метод (статистический) основан на представлении о том, что все вещества состоят из молекул, находящихся в хаотическом движении. Так как число молекул огромно, то можно, применяя законы статистики, найти определенные закономерности для всего вещества в целом.

Термодинамический метод исходит из основных опытных законов, получивших название законов термодинамики. Термодинамический метод подходит к изучению явлений подобно классической механике, которая базируется на опытных законах Ньютона. При таком подходе не рассматривается внутреннее строение вещества.

Основные положения молекулярно-кинетической теории

И их опытное обоснование. Броуновское движение.

Масса и размер молекул.

Теорию, которая изучает тепловые явления в макроскопических телах и объясняет зависимости внутренних свойств тел от характера движения и взаимодействия между частицами, из которых состоят тела, называют молекулярно-кинетической теорией (сокращённо МКТ) или просто молекулярной физикой.

В основе молекулярно-кинетической теории лежат три важнейшие положения:

Согласно первому положению МКТ, все тела состоят из огромного количества частиц (атомов и молекул), между которыми есть промежутки.

Атом – это электрически нейтральная микрочастица, состоящая из положительно заряженного ядра и окружающей его электронной оболочки. Совокупность атомов одного вида называют химическим элементом. В естественном состоянии в природе встречаются атомы 90 химических элементов, наиболее тяжёлым из которых является уран. При сближении атомы могут объединяться в устойчивые группы. Системы из небольшого числа связанных друг с другом атомов называют молекулой. Например, молекула воды состоит из трёх атомов (рис.): двух атомов водорода (Н) и одного атома кислорода (О), поэтому её обозначают Н₂О. Молекулыявляютсянаименьшими устойчивыми частицами данного вещества, 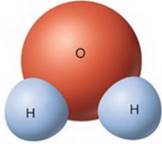обладающими его основными химическими свойствами. Например, наименьшая частица воды – это молекула воды, наименьшая частица сахара – молекула сахара.

Про вещества, состоящие из атомов, не объединённых в молекулы, говорят, что они находятся в атомарном состоянии; в противном случае говорят о молекулярном состоянии. В первом случае мельчайшей частицей вещества является атом (например Не), во втором случае – молекула (например Н₂О).

Если два тела состоят из одного и того же числа частиц, то говорят, что эти тела содержат одинаковое количество вещества. Количество вещества обозначается греческой буквой ν(ню) и измеряется в молях. За 1 моль принимают количество вещества в 12 г углерода. Так как в 12 г углерода содержится приблизительно 6∙10²³ атомов, то для количества вещества (т.е. числа молей) в теле, состоящем из N частиц, можно написать

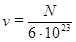моль. (1)

Если ввести обозначения N_A= 6∙10²³ моль^-1.

то соотношение (1) примет вид следующей простой формулы:

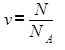(2)

Таким образом, количество вещества— это отношение числа N молекул (атомов) в данном макроскопическом теле к числу N_A атомов в 0,012 кг атомов углерода:

В 1 моле любого вещества содержится N_A = 6,02·10²³ молекул. Число N_A называют постоянной Авогадро.Физический смысл постоянной Авогадро заключается в том, что её значение показывает число частиц (атомов- в атомарном веществе, молекул –в молекулярном), содержащееся в 1 моле любого вещества.

Массу одного моля вещества называют молярной массой. Если молярную массу обозначить буквой μ, то для количества вещества в теле массой m можно записать:

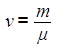(3)

Из формул (2) и (3) следует, что число частиц в любом теле можно определить по формуле:

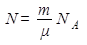(4)

Молярная масса определяется по формуле

М=М_г ·10^-3кг/моль

Здесь через М_г обозначена относительная молекулярная (атомная) масса вещества, измеренная в а.е.м. (атомные единицы массы), которой в молекулярной физике принято характеризовать массу молекул (атомов).Относительную молекулярную массуМ_г можно определить, если среднюю массу молекулы ( m_m) данного вещества разделить на 1/12 массы изотопа углерода ¹²С:

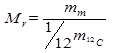
1/12 m¹²_C = 1а.е.м =1,66·10^-27 кг.

При решении задач эту величину находят с помощью таблицы Менделеева. В этой таблице указаны относительные атомные массы элементов. Складывая их в соответствии с химической формулой молекулы данного вещества, и получают относительную молекулярную М_г.Например, для

углерода (С) М_г=12·10^-3кг/моль

воды (Н₂О)М_г=(1·2+16)=18·10^-3кг/моль.

Аналогично определяется и относительная атомная масса.

Моль газа при нормальных условиях занимает объем V₀ = 22,4·10²³ м³

Следовательно, в 1 м³ любого газа при нормальных условиях (определяемых давлением Р=101325 Па =10⁵Па=1атм; температурой 273ºК (0ºС), объёмом 1 моля идеального газа V₀=22,4 10^-3м³) содержится одинаковое число молекул:

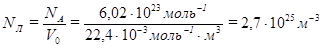
Это число получило название постоянной Лошмидта.

Чётких границ молекулы (как и атомы) не имеют. Размеры молекул твёрдых тел можно ориентировочно оценить следующим образом:

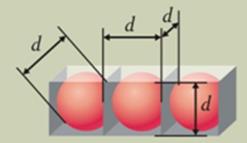
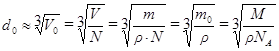
где 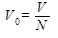- объём приходящийся на 1 молекулу, 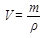- объём всего тела,

m и ρ – его масса и плотность, N – число молекул в нём.

Атомы и молекулы нельзя увидеть невооружённым глазом или с помощью оптического микроскопа. Поэтому сомнения многих учёных конца XIX в. в реальности их существования понять можно. Однако в XX в. ситуация стала иной. Сейчас с помощью электронного микроскопа, а также средств голографической микроскопии можно наблюдать изображение не только молекул, но даже отдельных атомов.

Данные рентгеноструктурного анализа показывают, что диаметр любого атома имеет порядок d = 10^-8 см (10^-10 м). Размеры молекул больше размеров атомов. Поскольку молекулы состоят из нескольких атомов, то чем больше количество атомов в молекуле, тем больше её размер. Размеры молекул лежат в пределах от 10^-8 см (10^-10 м) до 10^-5 см (10^-7 м).

Массы отдельных молекул и атомов очень малы, например абсолют­ное значение массы молекулы воды порядка 3·10^-26 кг. Массу отдельных молекул экспериментально определяют с помощью специального прибора – масс-спектрометра.

Кроме прямых экспериментов, позволяющих наблюдать атомы и молекулы, в пользу их существования говорит и множество других косвенных данных. Таковы, например, факты, касающиеся теплового расширения тел, их сжимаемости, растворения одних веществ в других и т.д.

Согласно второму положению молекулярно-кинетической теории,частицы непрерывно и хаотически (беспорядочно) движутся.

Это положение подтверждается существованием диффузии, испарения, давление газа на стенки сосуда, а также явлением броуновского движения.

Хаотичность движения означает, что у молекул не существует каких-либо предпочтительных путей и их движения имеют случайные направления.

Диффузия (от латинского diffusion – растекание, распространение) – явление, когда в результате теплового движения вещества происходит самопроизвольное проникновение одного вещества в другое (если эти вещества соприкасаются). Согласно молекулярно-кинетической теории, такое перемешивание происходит в результате того, что беспорядочно движущиеся молекулы одного вещества проникают в промежутки между молекулами другого вещества. Глубина проникновения зависит от температуры: чем выше температура, тем больше скорость движения частиц вещества и тем быстрее протекает диффузия. Диффузия наблюдается во всех состояниях вещества – в газах, жидкостях и твёрдых телах. Наиболее быстро диффузия происходит в газах (именно поэтому так быстро распространяется запах в воздухе). В жидкостях диффузия происходит медленнее, чем в газах. Это объясняется тем, что молекулы жидкости расположены значительно гуще, и потому «пробираться» через них значительно труднее. Медленнее всего диффузия происходит в твёрдых телах. В одном из опытов гладко отшлифованные пластины свинца и золота положили одна на другую и сжали грузом. Через пять лет золото и свинец проникли друг в друга на 1мм. Диффузия в твёрдых телах обеспечивает соединение металлов при сварке, пайке, хромировании и т.п. Диффузия имеет большое значение в процессах жизнедеятельности человека, животных и растений. Например, именно благодаря диффузии кислород из лёгких проникает в кровь человека, а из крови - в ткани.

Броуновским движением называют беспорядочное движение взвешенных в жидкости или газе мелких частичек другого вещества. Это движение было открыто в 1827 г. английским ботаником Р.Броуном, который наблюдал в микроскоп движение цветочной пыльцы, взвешенной в воде. В наше время для таких наблюдений используют маленькие части краски гуммигут, которая не растворяется в воде. В газе броуновское движение совершают, например, взвешенные в воздухе частицы пыли или дыма. Броуновское движение частицы возникает потому, что импульсы, с которыми молекулы жидкости или газа действуют на эту частицу, не компенсируют друг друга. Молекулы среды (то есть молекулы газа или жидкости) движутся хаотично, поэтому их удары приводят броуновскую частицу в беспорядочное движение: броуновская частица быстро меняет свою скорость по направлению и по величине (рис.1).

В ходе изучения броуновского движения было обнаружено, что его интенсивность: а) увеличивается с ростом температуры среды; б) увеличивается при уменьшении размеров самих броуновских частиц; в)уменьшается в более вязкой жидкости и г) совершенно не зависит от материала (плотности) броуновских частиц. Кроме того, было установлено, что это движение универсально (поскольку наблюдается у всех веществ, взвешенных в распыленном состоянии в жидкости), непрерывно (в закрытом со всех сторон кювете, его можно наблюдать неделями, месяцами, годами) и хаотично (беспорядочно).

Согласно третьему положению МКТ, частицы вещества взаимодействуют друг с другом: притягиваются на небольших расстояниях и отталкиваются, когда эти расстояния уменьшаются.

Наличие сил межмолекулярного взаимодействия (сил взаимного притяжения и отталкивания) объясняет существование устойчивых жидких и твёрдых тел.

Этими же причинами объясняется малая сжимаемость жидкостей и способность твёрдых тел сопротивляться деформациям сжатия и растяжения.

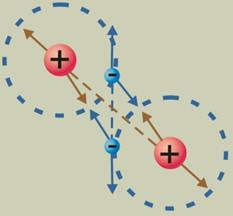Силы межмолекулярного взаимодействия имеют электромагнитную природу и сводятся к двум типам: притяжению и отталкиванию. Эти силы проявляются на расстояниях, сравнимых с размерами молекул. Причиной этих сил является то, что молекулы и атомы состоят из заряженных частиц с противоположными знаками зарядов – отрицательных электронов и положительно заряженных атомных ядер. В целом молекулы электрически нейтральны. На рисунке 2.2 с помощью стрелок показано, что ядра атомов, внутри которых находятся положительно заряженные протоны, отталкиваются друг от друга, так же ведут себя и отрицательно заряженные электроны. А вот между ядрами и электронами действуют силы притяжения.

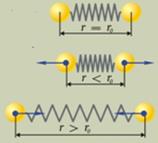Зависимость сил взаимодействия молекул от расстояния между ними качественно объясняет молекулярный механизм появления сил упругости в твёрдых телах. При растяжении твёрдого тела частицы удаляются друг от друга. При этом появляются силы притяжения молекул, которые возвращают частицы в первоначальное положение. При сжатии твёрдого тела частицы сближаются на расстояния. Это приводит к увеличению сил отталкивания, которые возвращают частицы в первоначальное положение и препятствуют дальнейшему сжатию.

Поэтому при малых деформациях (в миллионы раз превышающих размер молекул) выполняется закон Гука, согласно которому сила упругости пропорциональна деформации. При больших смещениях закон Гука не действует

О справедливости этого положения свидетельствует сопротивляемость всех тел сжатию, а также (за исключением газов) –их растяжению.

Основное уравнение молекулярно-кинетической теории идеальных газов

Объем газа всегда совпадает с объемом того сосуда, который он за­нимает.

Давление возникает в результате ударов молекул о стенки сосудов. Рассмотрим поведение одной произвольно выбранной молекулы и иде­ального газа, находящейся в сосуде, имеющем форму куба (рис. 2.8). Пусть υ_i-ее скорость, направленная перпендикулярно стенке сосуда, а m_i — масса. При упругом ударе молекула сообщает стенке импульс m_iυ_i после удара ее импульс станет равным - m_iυ_i. Следовательно, импульс молекулы изменится на m_iυ_i-(-m_iυ_i)= 2m_iυ_i. По второму закону Ньютона,

F_it_i =2 m_iυ_i. (2.22)

Если в кубе, длина ребра которого равна ℓ, находится n молекул, то вследствие беспорядочного движения молекул и равновероятности всех направлений можно считать, что 1/3N молекул движется вдоль оси X, 1/3N— вдоль оси Y, 1/3N молекул — вдоль оси Z. Чтобы найти среднюю силу дав­ления газа, следует подсчитать сумму импульсов всех молекул, ударяющих­ся о стенку за определенное время. От удара до следующего удара о ту же грань молекула проходит путь, в среднем равный 2ℓ. Интервал времени меж­ду двумя этими ударами равен t_i = 2ℓ/υ_i. Определим теперь среднюю силу, с которой действует на одну из стенок сосуда одна молекула. В уравнение (2.22) подставим время t_i между двумя ударами:

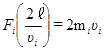
откуда

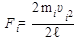или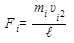

Молекулы газа движутся с различной скоростью (υ₁, ..., υ_i, ..., υ_n); следовательно, они сообщают стенке сосуда и раз­личные импульсы. Выберем какое-либо одно направление движения молекул (например, вдоль оси X). Между двумя противоположными гранями куба в этом направ­лении движется 1/3 всех молекул, и суммарная сила ударов об одну грань

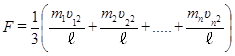
В идеальном газе m₁ = m₂ = ... = m_n = m, поэтому

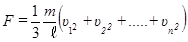
Умножив и разделив правую часть равенства на N, получим

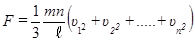
Выражение, стоящее в скобках, есть квадрат средней квадратической скорости движения молекул 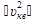. Таким образом,

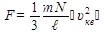
Cледовательно,

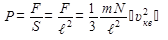
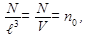
Тогда

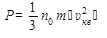
Это основное уравнение молекулярно-кинетической теории.

Оно определяет макроскопическую величину — давление газа через концентрацию n₀ молекул, массу m отдельных молекул и среднюю квадратическую скорость 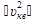их движения.

Если через 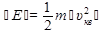обозначить среднюю кинетическую энергию поступательного движения некой «средней» молекулы, то уравнение (2.25) можно записать в виде

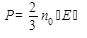
Давление газа равно 2/3 от средней кинетической энергии поступа­тельного движения всех молекул, которые содержатся в единичном объ­еме газа.

Следствия, вытекающим из основ­ного уравнения молекулярно-кинетической теории газов.

Ø Возьмем 1 моль газа, который занимает объем V. Плотность молекул газа 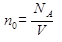и уравнение (2.26) можно записать в виде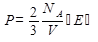

Но для 1 моль справедливо уравнение состояния рV = RТ, откуда

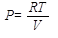
Подставив это выражение для давления в уравнение (2.27) и решив его относительно Т или 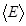, получим:

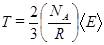(2.28)

Из уравнения (2.28) следует, что термодинамическая температура пропорциональна средней кинетической энергии хаотического дви­жения молекул газа.

Ø Чем быстрее движутся молекулы, тем выше температура. Из уравне­ния (2.28) находим

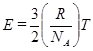(2.28а)

для любого газа, откуда следует:средняя кинетическая энергия молекул разных газов, находящихся при одинаковой температуре, равна между собой.

Из равенства средних кинетических энергий газовых молекул следу­ет, что при перемешивании различных газов, имеющих одинаковые тем­пературы, не происходит преимущественной передачи энергии от моле­кул одного газа молекулам другого.

Величина 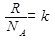получила название постоянной Больцмана и представляет собой газовую постоянную, отнесенную к одной молекуле:

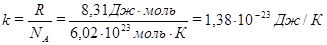
Следовательно, выражение (2.28а) можно представить в виде

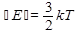(229)

Ø Подставляя (2.29) в (2.26), находим выражение для давления газа:

Р = n₀kТ (230)

Давление газа пропорционально произведению числа молекул в единице объема на его термодинамическую температуру.

Анализ уравнения (2.29) показывает, что при Т=0К кинетическая энергия поступательного движения молекул Е=0, а следовательно, и 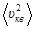= 0. Таким образом, при Т = 0 К отсутствует поступательное движение молекул.

Однако это не означает, что при Т=0К прекращается движение во­обще. Сохраняются вращательное и колебательное движения атомов и молекул. По современным представлениям, при Т=0К у атомов и еще более мелких частиц остается некоторая энергия, называемая нулевой.

Представим теперь формулу (2.29) в виде

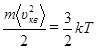
откуда средняя квадратическая скорость

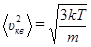(2.31)

Отсюда следует: средняя квадратическая скорость молекул пропорциональ­на корню квадратному из термодинамической температуры.

На основании выражения (2.29) мож­но установить определение температуры: термодинамическая температу­ра с точностью до постоянного множителя 3/2k равна средней кинетиче­ской энергии поступательного движения молекулы идеального газа.