Основное уравнение кинетической теории газов

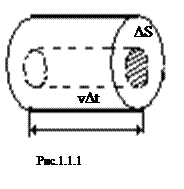Для вывода этого уравнения предположим, что в сосуде находится идеальный газ. Молекулы газа соударяются друг с другом и со стенками сосуда. Соударения молекул друг с другом приводят только к перераспределению энергии между молекулами. Выделим некоторую элементарную площадку на стенке сосуда и рассчитаем давление газа на нее (Рис.1). При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс 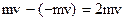, где m - масса молекулы, v - ее скорость. За время Dt площадки DS достигнут только те молекулы, которые заключены в объеме цилиндра с основанием DS и высотой vDt. Если n - концентрация молекул, то число этих молекул - nDSvDt. Однако следует учесть, что молекулы движутся к площадке DS под разными углами и с различными скоростями. Поскольку движение молекул хаотическое, то его можно заменить движением вдоль трех взаимно перпендикулярных направлений. К тому же поскольку ни одно из направлений не имеет преимуществ перед другими, то в любой момент времени вдоль каждого из них движется 1/3 всех молекул, причем половина из них, т.е. 1/6 в одну сторону, другая половина - в противоположную. Тогда за время Dt площадку DS достигнет число молекул, равное 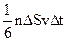. При столкновении с площадкой DS эти молекулы передадут ей импульс

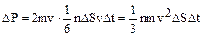
Тогда давление, оказываемое газом на стенку сосуда, равно

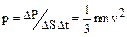. (1.1.1)

Как уже отмечалось выше, молекулы движутся с различными скоростями v_1, v₂,…, v_n, если в объеме V газа содержится N молекул, то вместо скорости v необходимо учитывать среднюю квадратичную скорость

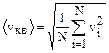
Тогда уравнение (1.1.1) запишется в виде

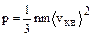
(1.1.2)

Уравнение (1.1.2) называют основным уравнением кинетической теории идеальных газов.

(1.1.3)

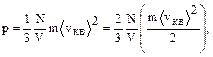Поскольку концентрация n=N/V, следовательно

или ,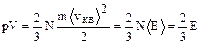

где áЕ ñ- средняя кинетическая энергия одной молекулы, Е - кинетическая энергия газа.

Давление пропорционально числу молекул в единице объема и среднему значению кинетической энергии молекул.

Из основного уравнения можно вывести все газовые законы, установленные экспериментально еще в XVIII столетии, для данной массы газа справедливы законы:

Бойля-Мариотта PV=const, при T=const;

Гей-Люссака 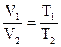при р=const и 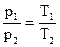при V=const;

Дальтона p=p₁+p₂+…+p_n;

Для 1 киломоля идеального газа справедлива формула Клапейрона-Менделеева

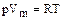, (1.1.4)

где R=8,314 Дж/(мольК) - универсальная газовая постоянная. Для одного моля газа N=N_A=6,02×10²³ - число Авагадро. Следовательно, число Авогадро это число молекул в моле любого вещества. Количество молекул газа при нормальных условиях (p=1,013€10^-5 Па, T=273°K), находящихся в единице объема (1м²), называется числом Лошмидта N_L=2,687×10 ²⁵м^-3. Оно равняется числу Авогадро, деленному на объем моля газа при нормальных условиях V_m=22,41×10^-3м³×моль^-1

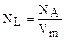
Сравнивая выражения (1.1.3) и (1.1.4), получаем

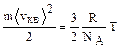
С учетом постоянной Больцмана (k=R/N_A=1,38×10^-23Дж/K):

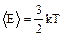(1.1.5)

Мы получили соотношение, связывающее среднюю кинетическую энергию одной молекулы с температурой.

Температура - физическая величина, характеризующая состояние равновесия термодинамической системы и пропорциональная средней кинетической энергии хаотического движения частиц, составляющих систему.

При приведении в контакт веществ, с различными температурами, т.е. кинетическими энергиями частиц, имеет место теплообмен - выравнивание температур.

Для измерения температуры используют зависимость физических свойств веществ от температуры (контактную разность потенциалов, тепловое расширение, зависимость электрического сопротивления, излучательную способность и т.д.).

Из уравнения (1.1.4) можно рассмотреть связь между температурой, давлением и объемом для заданной массы идеального газа

,

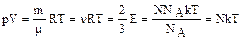где m - масса газа,

m - молярная масса газа,

n - число молей,

N- число молекул в данном объеме газа.

Поскольку для двух различных состояний одной массы газа p₁V₁=NkT₁ и p₂V₂=NkT₂, имеем 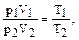т.е. 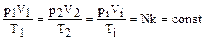(1.1.6)

Термодинамическая температура прямо пропорциональна произведению объема на давление ( для заданной массы газа).

В качестве примера применения уравнения Менделеева - Клапейрона рассмотрим процесс изменения температуры и давления при постоянном объеме V=const (изохорический процесс). В этом случае удобно воспользоваться зависимостью давления от плотности и температуры

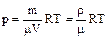, (1.1.7)

где r=m/m - плотность газа (кг/м³).

Рис.1.1.2

График изохорического процесса в координатах р,Т (рис.1.1.2) представляет собой прямые, проходящие через начало координат. Из зависимости (1.1.7) и графика следует, что большей плотности r (или концентрации n) соответствует большее давление. С другой стороны, большему объему V (при постоянной массе m) соответствует меньший угол наклона прямой к оси абсцисс - обратная зависимость.

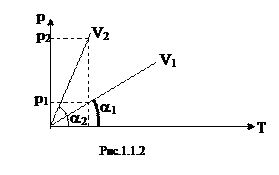
Пример 1. Определить температуру, при которой 4м² газа создают давление 1,5×10⁵ Па, если при нормальных условиях газ занимает объем 5м³.

Решение. В нормальных условиях V₁=5 м³, р₁=1атм=101325 Па, Т₁=273°К, необходимо найти Т₂ при V₂=4м³, р₂=1,5×10⁵ Па. Согласно (5) имеем

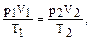откуда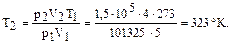

Пример2. Сколько молекул вы вдыхаете, если при одном вдохе получаете 1л воздуха?

Решение. Объем одного киломоля равен 22,4м³, значит 1л воздуха равен 1×10^-3/22,4=4,5×10^-5кмоль. Таким образом, 1л воздуха содержит 4,5×10^-5×6,02×10²⁶=2,7×10²² молекул.

Пример3. Что тяжелее 1м³ сухого воздуха или 1м³ влажного воздуха при одинаковых температурах и давлениях? m_возд.=29 кг/кмоль, m_воды=18 кг/кмоль.

Решение. Средняя масса молекулы сухого воздуха больше, чем у водяного пара. Число молекул в обоих случаях одинаково, но во влажном воздухе часть молекул заменена более легкими молекулами воды, следовательно, 1м³ сухого воздуха тяжелее, чем 1м³ влажного.

Пример4. Как изменится давление данной массы газа при постоянном объеме, если температуру газа увеличить в 2 раза и каждая молекула при этом распадется на два атома?

Решение. 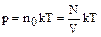, так как N и T увеличиваются в 2 раза, то давление увеличится в 4 раза.

Пример5. Показать, что .

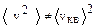Решение. Рассмотрим четыре молекулы, скорости которых различны и равны 1,2,3 и 4м/c. Квадрат среднего значения 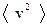равен

,

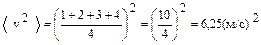а средняя квадратичная скорость равна

.

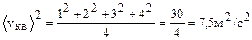Если скорости отдельных молекул равны +1, -2, -3, +4 м/c, то 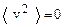, а

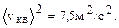
Вероятность

Основой статистического метода служит теория вероятностей. Теория вероятностей в абстрактной форме отражает закономерности, присущие случайным событиям массового характера. Их отличительная черта состоит в том, что при многократном повторении в неизменных условиях некоторого испытания могут осуществляться различные события. Испытанием в теории вероятностей принято называть осуществление точно установленных предписаний и условий, которые принципиально могут воспроизводится неограниченное число раз. Результат испытания называется событием. Случайным называется событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти. Например, если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись. Следовательно, событие " при бросании монеты выпал "герб" - случайное. Каждое случайно событие - следствие действия очень многих случайных причин, поскольку учесть влияние на результат всех этих причин невозможно, то нельзя предсказать исход одиночного случайного события. Однако если рассматривать случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий, то они подчиняются определенным закономерностям - вероятностным закономерностям.

Числовая характеристика возможности появления какого-либо определенного случайного события называется вероятностью.

Если при N опытах n раз произошло определенное событие А, то величина

p(А)=n(А)/N

называется относительной частотой появления этого события в серии испытаний. В общем случае величина р(А) колеблется при переходе от одной серии испытаний к другой. Однако, если N®¥, то относительная частота стремится к некоторому предельному значению, которое называется вероятностью события А.

Под вероятностью понимается предел, к которому стремится относительная частота появления некоторого события при достаточно большом, стремящемся к бесконечности числе повторений опыта при неизменных внешних условиях.

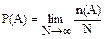(1.2.1)

Таким образом, вероятность некоторого события А всегда можно приближенно определить с точностью до заранее заданной сколь угодно малой отличной от нуля величины, если провести достаточно большое, но конечное число испытаний.

События могут состоять и в появлении того или иного числа. Например, при бросании игральной кости могут появиться число 1, 2, 3, 4, 5, и 6. Наперед, определить число выпавших очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная; числа1, 2, 3, 4, 5, и 6 есть возможные значения этой величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, заранее неизвестное.

Из определения следует, что численное значение вероятности заключено между 0 и 1

.

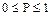Событие, которое всегда происходит при данных условиях. называется достоверным, событие, которое никогда не происходит при данных условиях, называется невозможным.

Определение относительной частоты приводит к выражению среднего значения любой физической величины А.

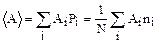(1.2.2)

Их определения же следует, что сумма вероятностей, т.е. вероятность того, что случайная величина примет какое-то значение, равна1.

.

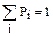Это условие называется условием нормировки.

Рассмотрим некоторую систему, которая может находиться в определенных состояниях.Представим, что мы производим наблюдения в следующие друг за другом моменты времени t₁, t₂, …, причем число таких наблюдений велико и равно N. При каждом наблюдении система оказывается в одном из своих состояний. Обозначим через N_i число случаев, когда при наблюдении система находилась в состоянии с индексом i, тогда вероятность того, что система будет находится в состоянии N_i, приблизительно равна

.

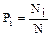Часто встречаются системы, состояние которых изменяется не дискретно, а непрерывно. В состоянии, в котором величина А имеет значение А_i система будет находиться бесконечно малое время. В таком случае следует говорить о вероятности того, что система находиться в состоянии, для которого величина А имеет значения, лежащие в интервале от А до А+dA. В этом случае вероятность можно выразить следующим образом:

,

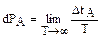где Dt_A - время , в течение которого система находится в состояниях, соответствующих значениям А, лежащим между А и А+dA. Как время Dt_A, так и вероятность dP_A будут пропорциональны величине интервала dA. Следовательно dP_A можно представить в виде

,

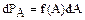где f(A) - вероятность того, что значение А лежит в некотором единичном интервале. Функция f(А) называется плотностью вероятности и используется в тех случаях, когда случайная величина А изменяется непрерывно.

Пример6. Материальная точка колеблется по закону 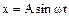. Найти вероятность того, что при случайном измерении ее положения она будет обнаружена в интервале x, x+dx.

Материальная точка совершает периодическое движение, полное время наблюдения можно связать с периодом колебаний Т. Если dt - время, в течение которого материальная точка находится в интервале х, х+dx, то искомая вероятность равна

dP=2dt/T.

Множитель2 введен потому, что за период Т точка побывает в указанном интервале дважды. Выражая время dt через dx, и учитавая, что Т=2p/w, имеем

,

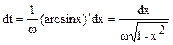следовательно,

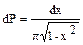- искомая вероятность.

В системах, состоящих из сравнительно небольшого числа частиц, имеют место отклонения физических величин, характеризующих системы, от их средних значений, такие отклонения называются флуктуациями.

Рассмотрим некоторую величину, которая характеризует отклонения истинных значений величины А от ее среднего значения 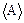. Можно попытаться в качестве критерия взять среднее значение разности 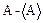, т.е. 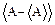. Обычно эта величина равна 0:

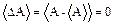
Равенство нулю величины 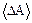выражает тот факт, что отклонения А от 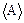происходит одинаково часто как в сторону больших, так и в сторону меньших значений. Вследствие этого в качестве критерия необходимо взять не среднюю разность, а средний квадрат разности 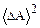. Он не зависит от направления отклонения. Данная величина 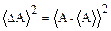называется квадратичной флуктуацией. Это существенно положительная величина.На основании определения :

.

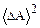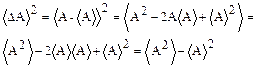Для оценки относительной погрешности при замене А ее средним значением, служит величина

,

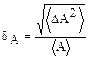которую называют относительной флуктуацией.

Из соотношений теории вероятностей следует очень важная связь флуктуаций с количеством частиц N, находящихся в рассматриваемой системе

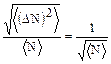(1.2.3)

Относительная роль флуктуаций уменьшается с увеличением числа частиц в системе. Вследствие этого в макроскопических системах величина относительной флуктуации незначительна и с достаточной точностью все макроскопические параметры системы равны их средним значениям.

Флуктуации имеют очень большое значение не только в физике, но и в технике. Например, при протекании тока в проводниках, полупроводниковых и электронных устройствах возможны флуктуации плотности и скорости частиц - носителей заряда. Следствием этого являются так называемый дробовой эффект, тепловой шум. В этом случае флуктуации ограничивают точность измерения электрических величин.

Подобные эффекты возникают не только при измерении электрических величин, но и для любой измерительной техники, так как оно устанавливает нижнюю границу точности измерений, которая является принципиальной, обусловленной самой природой вещей.

Распределение Максвелла

В равновесном состоянии в системе, состоящей из огромного числа частиц, например в некотором объеме газа, при отсутствии внешних воздействий не происходит макроскопических изменений: параметры системы остаются постоянными. Постоянным остается и среднее значение скорости молекул. Ответ на вопрос, сколько молекул, или какая их часть движется с определенной скоростью в данный момент, был теоретически получен Максвеллом.

Введем понятие пространства скоростей. Для каждой молекулы откладываем компоненты ее скорости по трем взаимно перпендикулярным осям (рис. 1.3.1).

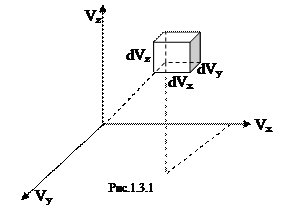
Каждая точка в пространстве скоростей соответствует одной молекуле с определенной скоростью. Вектор скорости идет от начала координат к рассматриваемой точке.

Рассмотрим, как будут распределены молекулы, содержащиеся в единичном объеме газа по скоростям.

Эти молекулы будут изображаться совокупностью из n точек. Из-за столкновений молекул какие-то точки будут выходить из элемента объема, а другие входить в него. Однако среднее число точек в данном элементе объема сохраняется.

Закон Максвелла описывается некоторой функцией f(v), которая называется функция распределения молекул по скоростям. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, т.е.

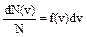, откуда .

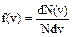Применяя методы теории вероятностей, Максвелл нашел эту функцию:

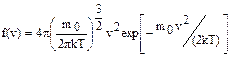(1.3.1)

Из формулы видно, что конкретный вид функции зависит от рода газа (от массы молекулы m₀) и от параметра состояния (температуры T).

График функции f(v) приведен на рис.1.3.2. Функция f(v) начинается от нуля, достигает максимума при v_в и затем асимптотически стремится к нулю. Кривая не симметрична относительно v_в.

Распределение Максвелла - это распределение по скоростям молекул идеального газа, находящегося в состоянии термодинамического равновесия.

Интегрируя распределение Максвелла, можно рассчитать средние величины. Средний квадрат скорости (средняя квадратичная скорость)

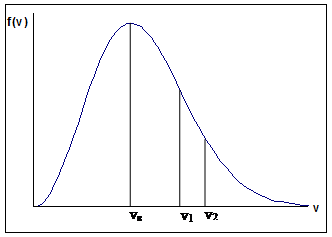
Рис.1.3.2.

Рис.1.3.2

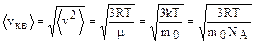1.3.2)

vв

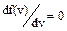Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Значение наиболее вероятной скорости можно определить, используя условие максимума функции откуда следует, что

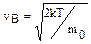(1.3.3)

Для того, чтобы найти число молекул, обладающих скоростями в интервале от v₁ до v₂, необходимо определить площадь под соответствующим участком кривой (рис.1.3.2.)

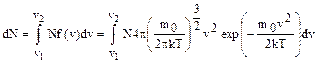
При увеличении температуры максимум кривой Максвелла смещается в сторону больших скоростей и вид кривой изменяется. Распределения для двух разных температур приведены на рис.1.3.3. Поскольку площадь, ограниченная кривой, остается неизменной, следовательно, при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться.

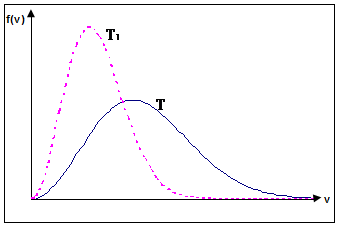Рис.1.3.3 Т₁< Т.

Среднее значение абсолютной величины скорости (среднее значение скорости равно нулю, так как отрицательное и положительное значения компонент равноправны) определяется по формуле

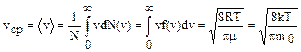(1.3.4)

Таким образом, скорости, характеризующие состояние газа:

1) наиболее вероятная ;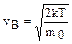

2) средняя скорость ;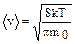

3) средняя квадратичная .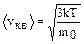

Эти скорости связаны соотношением

v_В : ávñ : áv_квñ @1:1,13:1,22,

то есть средняя квадратичная скорость имеет наибольшую величину.

Исходя их распределения молекул по скоростям, перейдя к новой переменной Е=m₀v²/2, можно получить функцию распределения молекул по энергиям

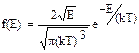(1.3.5)

Тогда средняя кинетическая энергия молекулы идеального газа равна

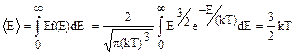(1.3.6)

Для того, чтобы рассчитать количество молекул DN, скорости которых находятся в промежутке от v до v+Dv, удобно ввести относительную скорость u=v/v_В, где v_{В -} наиболее вероятная скорость. Тогда DN - число молекул, относительные скорости которых находятся в интервале u, u+Du, т.е. v/v_в, v+Dv/v_В, где должно быть Dv†v. Таким образом, имеем

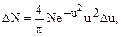
где N - полное число молекул газа, DN/N - относительное число (доля) молекул, имеющих скорости в интервале u, u+Du. График этой зависимости соответствует рис.1.3.2, если по оси абсцисс отложить u, а по оси ординат величину DN/(NDu) - функцию распределения.

Пример7. Определить среднеквадратичную скорость молекул азота при температуре 27°С. Как зависит средне квадратичная скорость от молекулярной массы и температуры?

Т=300°К, m=28 кг/кмоль, k=1,38×10^-23Дж/град.

Решени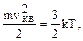е. где ;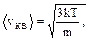

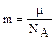Таким образом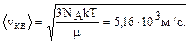

Средняя квадратичная скорость прямо пропорциональна корню квадратному из температуры и обратно пропорциональна корню квадратному из молекулярной массы.