Розрахунок енергії Фермі. Середнє значення енергії елек-тронного газу в металі. Температура виродження

Щоб розрахувати максимальну енергію електронів у металі, тобто енергію Фермі, а також середнє значення енергії вільних електронів в енергетичній зоні металу, можна використати формулу (2.1.7).

Для знаходження загального числа всіх електронів в енергетичній зоні металу в праву частину цієї формули слід підставити вирази густини квантових станів і імовірності заповнення цих станів електронами та проінтегрувати цей вираз за значеннями енергій від 0 до Е_ф

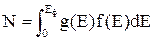(2.6.2)

де g(E) ― густина квантових станів в енергетичній зоні; f(E) – імовірність заповнення цих станів електронами (розподіл Фермі-Дірака); dE – енергетичний інтервал.

При абсолютному нулі температур f(E)=1, тому:

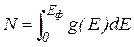. (2.6.3)

Густина квантових станів для електронів провідності в металі дорівнює

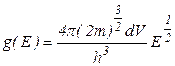. (2.6.4)

Підставивши (2.6.4) в (2.6.3) одержимо:

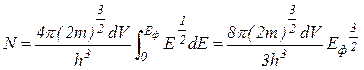. (2.6.5)

Концентрація електронів провідності в енергетичній зоні буде дорівнювати

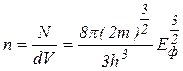. (2.6.6)

Концентрацію електронів провідності легко розрахувати засобами молекулярної фізики, тобто

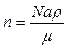, (2.6.7)

де Na ― число Авогадро; r ― густина металу; m ― молярна маса металу.

Для прикладу знайдемо концентрацію вільних електронів провідності в міді

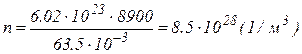. (2.6.8)

Підставляючи (2.6.7) в (2.6.6) легко розрахувати енергію Фермі для міді

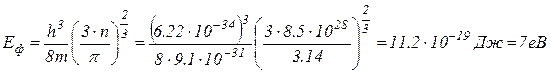
Аналогічні розрахунки показують, що різні метали мають відповідно різні значення енергії Фермі. Так енергія Фермі калію 2,14 еВ, енергія Фермі срібла 5,5 еВ, енергія Фермі алюмінію 11,9 еВ, тощо.

Середнє значення енергії електронів провідності в металі можна розрахувати діленням сумарної енергії всіх електронів в енергетичній зоні на їх число в цій зоні, тобто

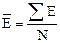. (2.6.9)

Сумарну енергію всіх електронів у енергетичній зоні металу можна розрахувати засобами теорії імовірності, тобто

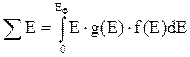, (2.6.10)

де g(E) ― густина квантових станів у виділеній частині енергетичної зони в області енергій Е; f(E) ― імовірність заповнення цих станів електронами.

При абсолютному нулі температур (Т=0)f(E)=1, тому

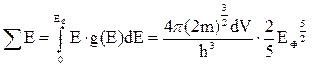. (2.6.11)

Середнє значення енергії електронів знайдемо, поділивши (2.6.11) на (2.6.5), тобто

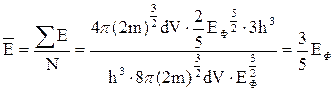. (2.6.12)

Таким чином середня енергія електронів провідності в міді при Т=0 не перевищує 4,2еВ.

Електронний газ в металі принципово відрізняється від класичного ідеального газу. Основна відмінність полягає у незалежності енергії електронів від температури. Цю властивість електронного газу називають виродженням. Температура, при якій електронний газ перестає бути квантовим, тобто виродженим, називається температурою Фермі.

Температуру виродження електронного газу знайдемо із співвідношення

кT_Ф=Е_Ф, (2.6.13)

Звідки

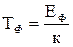(2.6.14)

Розрахунок температури Фермі для міді

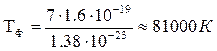. (2.6.15)

Таким чином електронний газ в міді залишається виродженим, тобто квантовим, аж до температури 81000К. Для алюмінію така температура сягає 138000К. Вище температури Кюрі електронний газ втрачає квантові властивосі, тобто стає класичним.