Необходимые габариты безэховых камер

Затраты на создание безэховых камер во многом зависят от их габаритов. Поэтому определение технически обоснованных га­баритов, минимальных для проведения измерений с заданной точ­ностью, представляет практически важную задачу.

Длина безэховой камеры во многих случаях соответствует длине линии связи, необ­ходимой при измерениях. Поперечные размеры, как правило, определяются условиями обеспечения не­обходи­мой безэховости. От ми­нимального соотно­шения попе­реч­ных и про­дольных размеров БЭК зависит в зна­чи­тельной мере стои­мость камеры, а в ряде случаев сама возмож­ность реа­лиза­ции данных измерений в БЭК.

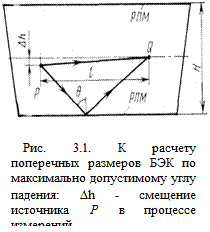
Для определения попе­речных размеров БЭК в работе [7] принят крите­рий, по кото­рому углы па­дения q поля на продоль­ные поверхности камеры не должны превышать максимального угла q_max, огово­ренного в документации на поглощающий материал (рис. 3.1).

Если l — длина линии связи между источником Ри точкой наблюдения Q, Dh — поперечные перемещения антенны, то шири­на камеры должна быть

H ³ l/tgq_max +Dh (3.1)

Для современных отечественных и зарубежных РПМ q_max = 50... 60°. Следовательно, требуемая ширина БЭК в соответст­вии с выражением (3.1)

H ³ (0,84…0,58)×l + +Dh (3.2)

Необходимый поперечный размер камер примерно равен 0,6 ... 0,8 ее длины. Это соотношение может быть несколько улучшено применением камер рупорного типа, но при этом имеют ме­сто существенные ограничения по условиям запитки камеры и возможностям перемещения линии связи, о которых говорилось ранее. В тех случаях, когда в процессе измерений линия связи должна перемещаться в пространстве камеры, камеры с улучшен­ным соотношением длины к поперечным размерам (так называе­мые туннельные камеры) возможны лишь с профилем, имеющим значительную продольную неоднородность, например с профилем в виде поперечных диафрагм (рис. 3.2).

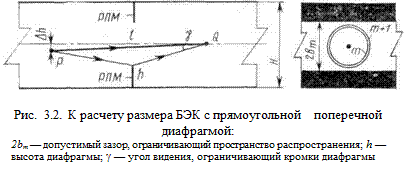При этом поглощающий материал располагается на плоскостях, перпендикулярных оси камеры, и ограничивающее соотношение (3.1) несправедливо. В этом случае, однако, необходимо обеспечить достаточный попереч­ный размер пространства распространения.

Пусть пространство ограничено противолежащими идеально поглощающими экранами. Тогда поле за экраном

U = U₀G_Фр

где U₀- поле в отсутствие экрана; G_Фр - коэффициент френелевского ослабления поля за счет ограниченности пространства. Для симметрично расположенной линии связи, как известно [80],

G_Фр= (е^ip/4/ 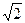)×2F( )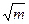

где 2F( 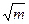)— интеграл Френеля; т — количество зон Френеля

в зазоре между экранами.

При перемещении точки наблюдения в пространстве камеры относительная величина колебаний амплитуды поля не должна превышать допустимой безэховости.

Условие допустимого ограничения пространства распростране­ния

çG_{Фр m} - G_{Фр m+2}÷ £ L_доп (3.3)

Из этого условия, заменяя для больших т интеграл Френеля пер­вым членом его асимптотического ряда, получим минимальное количество зон Френеля, которое необходимо обеспечить в зазоре между экранами,

çG_{Фр m} - G_{Фр m+2}÷ = 2 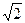/p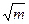

и

m ³ 8/p²L²_доп (3.4)

Минимально допустимое расстояние от оси камеры до кромки ограничивающего экрана равно размеру малой полуоси эллипса зоны Френеля:

b » 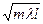/2 (3.5)

Подставляя (3.4) в (3.5) и обозначая через у угол между осью камеры и направлением на кромку ограничивающего экрана (рис. 3.2), получаем

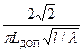tgg ³ (3.6)

При 1/l=100 даже для L_ДОП= —20 дБ получим tgg ³ 0,9.

Прямоугольная ограничивающая апертура не дает улучшения соотношения между поперечным и продольным размерами каме­ры. Улучшение этого соотношения возможно лишь при выполне­нии кромки ограничивающей апертуры в форме звездообразной ломаной линии, как показано, например, на рис. 3.3. В безэховую зону не попадает поле, рассеянное линейными отрезками кромки поглощающего экрана.

Для получения выражений типа (3.6), позволяющих опреде­лить требуемые соотношения между поперечными и продольными размерами безэховой камеры, воспользуемся решением в прибли­жении Кирхгофа задачи дифракции на «заостренной» идеально поглощающей полуплоскости — угловом плоском экране, не про­пускающем поле и тем ограничивающем пространство распро­странения.

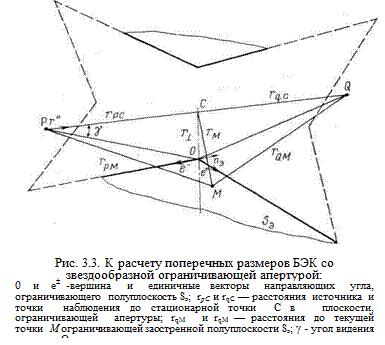Пусть в точке Р(рис. 3.3) расположен источник сферической волны, Q— точка наблюдения, S_Э — область пространства, пере­крытая экраном. Тогда относительное поле в точке приема

E(q) = 1 - E_Э(q)/E₀(q), (3.7)

где E₀(q)— неискаженное поле в точке Q(без экрана); E_э(q)— поле из области S_Э,дополнительной к области распространения.

В соответствии с принципом Гюйгенса—Френеля поле помехи за счет экранирования

E_Э(q)/E₀(q) ~ 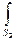A(r_м)e^iDF(rм)dS (3.8)

где A(r_м)— амплитудный множитель, учитывающий расхожде­ние сферической волны по пути r_ми r_с (рис. 3.3); DF(r_м)— раз­ность фаз прямого поля и поля из точек области S_Э.

Подынтегральное выражение (3.8) содержит быстроосцилли-рующий фазовый множитель. Поэтому вычисление интеграла можно проводить методом стационарной фазы. Разложим фазу подынтегрального выражения

DF(r_м) = к (r_PM + r_QM) - к (r_PC + r_QC) (3.9)

в ряд по r_мотносительно точки стационарной фазы Сна пересе­чении линии связи с плоскостью экрана.

По условию выбора точки стационарной фазы в разложении DF(r_M)наибольшим останется квадратичный член, который, как можно показать, зависит от r_^— расстояния точки Мповерхно­сти экрана до линии связи PQи приведенного расстояния r_сточек Ри Q до плоскости экрана. Тогда

DF (r_м) » к 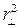/2 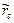(3.10)

где

r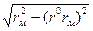_^ = ; (3.11)

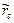= r_PC × r_QC/(r_PC + r_QC) ; (3.12)

к = 2p/l - волновой коэффициент;

r° — единичный вектор вдоль PQ.

Удобно перейти к интегрированию по проекции S_Эна пло­скость, перпендикулярную линию связи PQ, изменив одновременно масштаб.

Введя переменную вида

r = r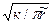_^ (3.13)

и вынося из под знака интеграла амплитудный множитель в точ­ке 0 вершины экрана, ближайшей к точке стационарной фазы С, получим вместо (3.8) интеграл по угловой области s_э

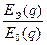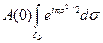~ ,(3.14)

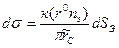, (3.15)

п — единичный вектор нормали к экрану.

На рис. 3.4 изображена область интегрирования s_э.

При проектировании на плоскость, ортогональную r°, орты е^± вдоль ребер S_Э переходят соответственно в т^± (см. рис. 3.4):

m^± = [e^± - r⁰ (e^± × r⁰)] / 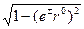. (3.16)

Как легко видеть, интеграл по s_э может быть вычислен как сумма интегралов по b⁺ и b^- — углам заострения составляющих полуплоскости. После интегрирования по угловой координате j вычисление поля помехи сводится к вычислению интеграла вида

J(r₀,r₁) = 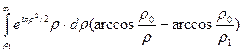, (3.17)

где р₀ и p₁ для области s_эпред­ставлены на рис. 3.4. Заметим, что в нашем случае p₀<p₁ для любых b ¹ p/2. Для случая р₀>>1 интеграл (3.17) может быть вычислен асимптотически. Для этого разложим arccos(p₀/p) в ряд Тейлора вблизи p₁ и ограничимся двумя членами разложения

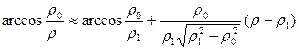. (3.18)

Подставляя (3.18) в (3.17), интегрируя по частям и переходя к асимптотике интеграла Френеля, получаем

J(r₀,r₁) » 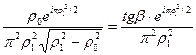. (3.19)

Подставляя из (3.13) значение r₁ получаем для поля помехи следующее выражение:

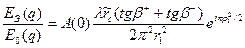. (3.20)

Из условия E_Э(q)/E₀(q) £ L_допполучим

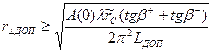. (3.21)

В случае симметричного расположения источника и точки наблюдения r_PC= r_QC= l₀/2, 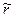= l₀/4 и b⁺ = b^- = b

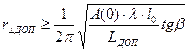(3.22)

или

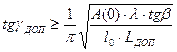. (3.23)

Для случая 1=100l, рассмотренного ранее, используя заострен­ный экран углом 2b=120°, получим для А(0)»1 из неравенства (3.23) для L_ДОП = -20 дБ tgg_доп ³ 0,2; для L_ДОП = -40 дБ tgg_доп ³ 0,6.

Итак, используя заостренные поперечные поглощающие экраны или пирамидальные рассеиватели, дающие звездообразный просвет поперечного сечения безэховой камеры, удается получить существенный выигрыш в соотношении длины камеры к ее поперечному сечению.

При отношении длины линии связи в камере к просвету попе­речного сечения 2:1 и 3: 1 для l = 100l, принципиально могут быть реализованы безэховости соответственно -40 и -30 дБ.