Деякі застосування термодинаміки

Теоретичні відомості

Термодинаміка випромінювання.Закони термодинаміки, як вже зазначалося, універсальні для довільних систем з достатньо великим числом частинок. Розглянемо термодинаміку квантів світла – фотонів, тобто термодинаміку електромагнітного випромінювання.

Нагадаємо, що випромінювання в деякій області простору, яке знаходиться у рівновазі з навколишніми тілами, називається тепловим або рівноважним. При тепловій рівновазі температури тіл вирівнюються. Тому теплове випромінювання, яке знаходиться у рівновазі з оточуючими тілами, має температуру цих тіл.

У термодинаміці рівноважне випромінювання – це система, що характеризується традиційними параметрами: об’ємом 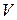, тиском 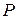, температурою .

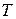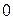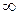З точки зору електродинаміки рівноважне випромінювання є неперервною сукупністю електромагнітних хвиль (з частотами від до ) від оточуючих це випромінювання частинок речовини. Амплітуди, фази, напрями цих хвиль розподілені за своїм спектром цілком хаотично.

Нехай 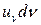– питома (в одиниці об’єму) енергія хвиль в інтервалі 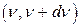. Величину 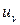називають спектральною густиною випромінювання. Тоді повну питому енергію 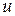випромінювання можна записати у вигляді

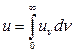. (9.1)

При цьому повна енергія 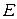в об’ємі 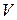(внаслідок ізотропності випромінювання) дорівнюватиме

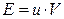. (9.2)

Аналогічно для ентропії маємо

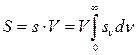. (9.3)

Важливою величиною вважається також енергія 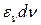хвиль (в інтервалі частот 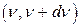), що випромінюється одиницею поверхні тіла за одиницю часу. При цьому 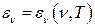називають спектральною енергетичною світністю. Величини 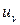та 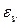пов’язані співвідношенням 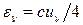, де 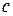– швидкість світла у вакуумі.

Нагадаємо відомі визначення. Тіла, які поглинають випромінювання всього спектра частот називаються абсолютно чорними або просто чорними. Тіла, які відбивають випромінювання всього спектра називають дзеркальними або білими. Тіла, які пропускають все випромінювання називають абсолютно прозорими. Зрозуміло, що тіл з абсолютними властивостями немає.

Кращим наближенням до абсолютно чорного тіла є достатньо малий отвір у стінці великої посудини. Багатократне відбивання випромінювання внутрішніми стінками посудини призводить до поглинання практично усього випромінювання, яке попадає у цей отвір, причому незалежно від речовини стінок. Тому такий отвір можна розглядати як випромінювач “чорного тіла” з частотним розподілом, що залежить лише від температури стінок.

У застосуванні до рівноважного випромінювання термодинаміка дозволяє встановити ряд закономірностей, серед яких найважливішим є закон Стефана–Больцмана. Одержимо його з основного рівняння термодинаміки для 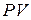–системи (3.13):

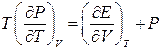. (9.4)

З електродинаміки відомо, що 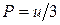. Підставляючи цей вираз у (9.4), з урахуванням (9.2) отримаємо диференціальне рівняння

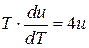, (9.5)

звідки знаходимо температурну залежність густини енергії 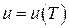випромінювання абсолютно чорного тіла:

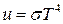. (9.6)

Стала інтегрування 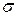називається сталою Стефана–Больцмана і визначається експериментально або методами статистичної фізики.

З (9.6) зразу можна записати термічне і калоричне рівняння рівноважного випромінювання:

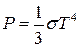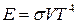; . (9.7)

Ентропію 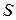знайдемо з :

,

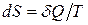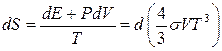звідки

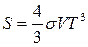, (9.8)

або

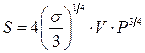. (9.9)

Теплоємність 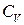отримаємо за допомогою формули :

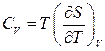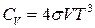. (9.10)

Оскільки з (9.7) 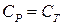, маємо

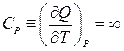. (9.11)

Термодинаміка магнетиків та діелектриків. Розглянемо поведінку систем: “магнетик у магнітному полі” та “діелектрик в електричному полі”. На ці системи, окрім тиску, діють також немеханічні сили.

Як буде далі видно є різні вирази для внутрішньої енергії та роботи намагнічування магнетика. Який саме вираз треба використовувати є несуттєвим, оскільки всі вони призводять до однакових результатів для властивостей магнетиків. Розглянемо це детальніше.

Відомо, що елементарна робота, виконувана одиницею об’єму магнетика при зміні в ньому індукції 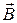магнітного поля, дорівнює

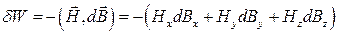
(зовнішнім параметром і незалежною змінною в даному випадку є індукція ).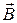

Для ізотропного магнетика, коли 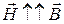, ця робота

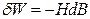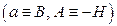, . (9.12)

Отже, якщо незалежною (магнітною) змінною є індукція 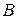, то основне рівняння термодинаміки для магнетика у магнітному полі матиме вигляд:

.

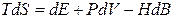Проте незалежними можуть виступати й інші два магнітних параметри – намагніченість 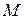магнетика та напруженість 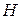поля, які зв’язані з індукцією 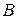(для ізотропного магнетика) рівнянням

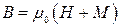. (9.13)

Знайдемо в цих випадках вирази для елементарної роботи намагнічування та основного рівняння термодинаміки. З урахуванням (9.13) елементарну роботу (9.12) можна записати двома способами:

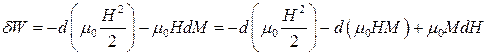, (9.14)

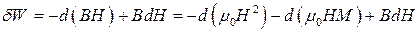. (9.15)

Перший доданок у правій частині (9.14) характеризує роботу збудження магнітного поля у вакуумі, другий – роботу проти зовнішнього магнітного поля, а третій доданок є роботою магнетика при намагнічуванні у власному смислі, коли внутрішнім параметром, спряженим із зовнішнім параметром 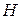, є намагніченість .

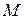Аналогічно, третій доданок у правій частині (9.15) можна інтерпретувати як роботу намагнічування у власному смислі, коли зовнішнім параметром виступає 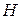, а внутрішнім – .

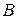У зв’язку з тим, що процес намагнічування магнетика в полі нерозривно пов’язаний з виникненням потенціальної енергії 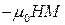магнетика у цьому полі, за роботу намагнічування магнетика у власному смислі приймають величину

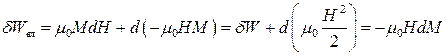. (9.16)

Тоді робота намагнічування 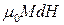дорівнюватиме сумі власної роботи намагнічування 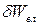та роботи 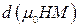проти зовнішнього поля:

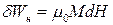. (9.17)

Робота намагнічування 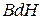дорівнюватиме різниці роботи 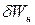та роботи 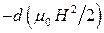збудження поля у вакуумі:

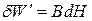. (9.18)

Провівши аналогічні міркування, отримаємо для системи “діелектрик в електричному полі” відповідні вирази для елементарної роботи поляризації:

, ,

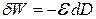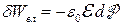(9.19)

,

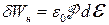
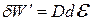де 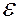– напруженість електричного поля; 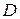– електричне зміщення (індукція електричного поля); 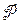– поляризованість діелектрика; 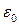– електрична стала.

Отже, основне рівняння термодинаміки для магнетика у магнітному полі матиме вигляд:

а) при незалежній (магнітній) змінній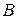

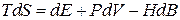; (9.20)

б) при незалежній змінній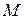

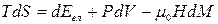, (9.21)

де 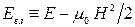– “власна” внутрішня енергія одиниці об’єму магнетика ( 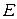без енергії поля у вакуумі);

в) при незалежній змінній 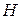, коли спряженою з нею величиною є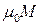

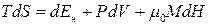, (9.22)

де 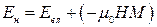– сума власної внутрішньої енергії магнетика та його потенціальної енергії у магнітному полі;

г) при незалежній змінній 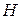, коли спряженою з нею величиною є індукція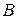

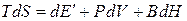, (9.23)

де 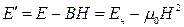– внутрішня енергія магнетика з урахуванням його потенціальної енергії у полі без енергії поля у вакуумі.

Вибір незалежної магнітної змінної залежить від характеру конкретної задачі та відповідає дослідженню системи з певною внутрішньою енергією 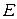, , 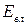, 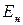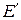. Для системи “діелектрик в електричному полі” аналогічні рівняння легко отримати після заміни магнітних змінних відповідними електричними.

Користуючись будь-яким з рівнянь (9.20) – (9.23), можна отримати вирази для диференціалів термодинамічних потенціалів магнетика. Так, з (9.21) знайдемо:

,

,

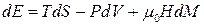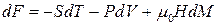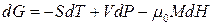, (9.24)

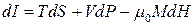, (9.25)

де літерою 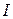позначено ентальпію, при цьому 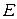, , 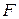, 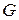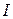означають відповідно , , , .

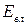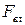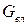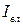Наведені вирази для термодинамічних потенціалів є основою для термодинаміки магнетиків (а при відповідній заміні магнітних величин електричними – діелектриків).

Для ілюстрації отримаємо з (9.24) зв’язок об’ємної магнітострикції з магнітопружним та п’єзомагнітним ефектами:

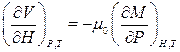. (9.26)

В останньому рівнянні 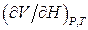характеризує зміну об’єму магнетика при зміні магнітного поля – об’ємна магнітострикція. При цьому похідна 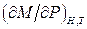характеризує зміну намагніченості зі зміною тиску. При наявності магнітного поля 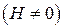це явище називається магнітопружним ефектом, а при відсутності поля 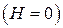– п’єзомагнітним ефектом.

Аналогічно, з рівняння для енергії Гіббса одиниці об’єму діелектрика

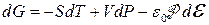
знайдемо зв’язок електрострикції, яка характеризується похідною 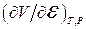, з п’єзоелектричним ефектом 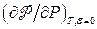, який полягає у зміні поляризації діелектрика при зміні зовнішнього тиску. Отримуємо:

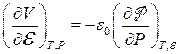. (9.27)

Зазначимо, що формула (9.27) відноситься до об’ємного п’єзоефекту, хоча у кристалах цей ефект, як правило, спостерігається вздовж певних кристалографічних напрямків.

Розглянемо також магнітокалоричний ефект, який полягає у зміні температури магнетика при зміні напруженості зовнішнього магнітного поля. При цьому найбільший практичний інтерес цей ефект має при адіабатному процесі зміні стану магнетика. Кількісну величину 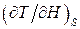розглядуваного ефекту можна знайти з (9.25):

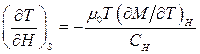, (9.28)

де 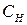– теплоємність при постійній напруженості магнітного поля.

Для парамагнетиків 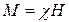. Згідно з законом Кюрі магнітна сприйнятливість 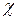обернено пропорційна до температури 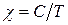, де 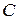– стала Кюрі 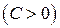. Тому 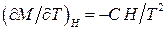. Отже,

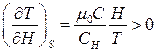. (9.29)

З (9.29) видно, що при розмагнічуванні 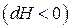температура знижується 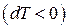. Відповідно до третього начала термодинаміки при 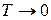К 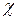перестає залежати від температури (див. задачу 7.1 розділу 7) і магнітокалоричний ефект зникає.