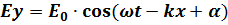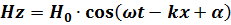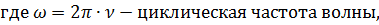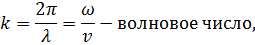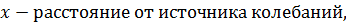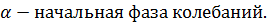Система уравнений Максвелла для электромагнитного поля.
Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле.
Первое уравнение Максвелла определяет источники электрического поля. Электрические заряды создают вокруг себя электрические поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.
Исходным для этого уравнения является уравнение Гаусса, которое говорит о том, что поток вектора 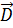 через замкнутую поверхность S равен заряду q, заключенному в данной поверхности:
через замкнутую поверхность S равен заряду q, заключенному в данной поверхности:
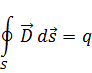
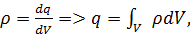 где ρ – объемная плотность заряда.
где ρ – объемная плотность заряда.
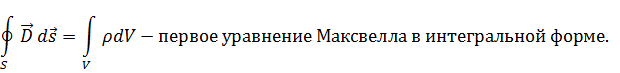
Для того чтобы получить дифференциальную форму, воспользуемся теоремой Гаусса-Остроградского, которая устанавливает связь между объемным и поверхностным интегралом:
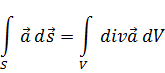
Дивергенция (расходимость) векторного поля – величина мощности источника поля.
Дивергенция является скалярной величиной:
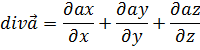
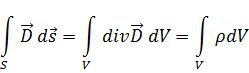
Данное равенство справедливо, если равны подынтегральные функции:
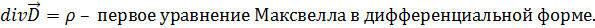
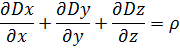
Второе уравнение Максвелла устанавливает для любых магнитных полей отсутствие свободных магнитных зарядов и то, что магнитные силовые линии всегда замкнуты. В интегральном виде этот факт записывается в виде уравнения:
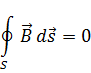
Поток вектора магнитной индукции через замкнутую поверхность равен нулю, поскольку магнитных зарядов одного знака в природе не обнаружено.
Применяя теорему Гаусса – Остроградского:
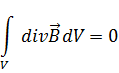
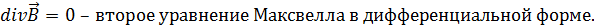
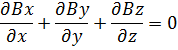
Третье уравнение Максвелла- это обобщение закона индукции Фарадея для диэлектрической среды в свободном пространстве
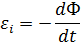
где Ф – поток магнитной индукции, пронизывающий проводящий контур и создающий в нем ЭДС.
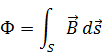
ЭДС создается не только в проводящем контуре, но и в некотором диэлектрическом контуре в виде электрического тока смещения.
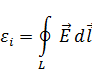
Физический смысл второго уравнения Максвелла состоит в том, что электрическое поле в некоторой области пространства связано с изменением магнитного поля во времени в этой области. Т.е. переменное магнитное поле порождает вихревое электрическое поле.
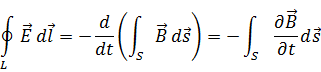
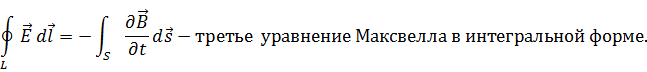
Воспользуемся уравнением Стокса, которое преобразует контурный интеграл в поверхностный:
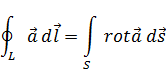
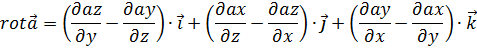
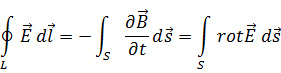
Данное равенство справедливо, если равны подынтегральные функции:
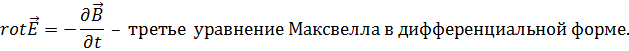
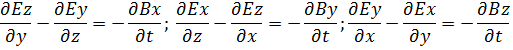
Четвертое уравнение Максвелла - это обобщение закона Ампера и Био-Саварра для токов смещения: циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему этот контур.
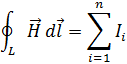
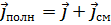
Физический смысл первого уравнения Максвелла состоит в том, что магнитное поле в некоторой области пространства связано не только с токами проводимости, протекающими в этой области, но и с изменением электрического поля во времени в этой области (токами смещения).
Циркуляция вектора 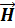 по контуру L равна сумме токов проводимости и смещения.
по контуру L равна сумме токов проводимости и смещения.
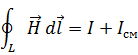
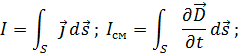
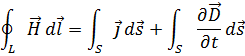
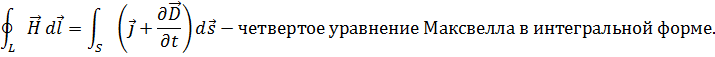
Получим дифференциальную форму уравнения Максвелла. Для этого воспользуемся уравнением Стокса, которое преобразует контурный интеграл в поверхностный:
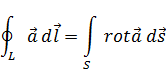
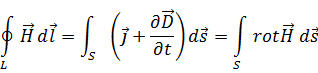
Данное равенство справедливо, если равны подынтегральные функции:
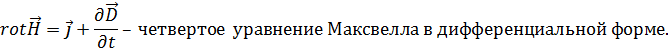
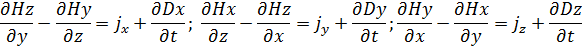
Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):
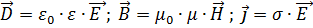
где 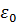 и
и 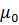 – соответственно электрическая и магнитная постоянная,
– соответственно электрическая и магнитная постоянная,
ε и μ – соответственно диэлектрическая и магнитная проницаемость,
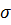 – удельная проводимость вещества.
– удельная проводимость вещества.
Уравнение плоской электромагнитной волны (ЭМВ). Поперечный характер ЭМВ. Амплитудные и фазовые соотношения. Скорость распространения электромагнитных волн в средах. Энергия электромагнитной волны. Вектор Пойнтинга.
Процесс распространения электромагнитных колебаний в пространстве называется электромагнитной волной. На электромагнитной волне колеблются векторы напряжённости 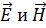 во взаимно перпендикулярных плоскостях в одной фазе – они одновременно обращаются в нуль и одновременно достигают максимальных значений.
во взаимно перпендикулярных плоскостях в одной фазе – они одновременно обращаются в нуль и одновременно достигают максимальных значений.
Различают плоские, сферические, цилиндрические и другие волны. Простейшими из них являются плоские волны. Плоскойназывается волна, у которой поверхности равных фаз – параллельные плоскости. Если поверхности равных амплитуд совпадают с поверхностями равных фаз, то такая волна называется однородной.
В однородной волне векторы 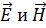 изменяются в пространстве только вдоль одного направления, перпендикулярно фазовому фронту этой волны и совпадающего с направлением ее распространения.
изменяются в пространстве только вдоль одного направления, перпендикулярно фазовому фронту этой волны и совпадающего с направлением ее распространения.
ЭМВ - это поперечные волны, т.е. векторы 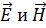 перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны.
перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны.
Исследуем плоскую ЭМВ, распространяющуюся в однородной нейтральной 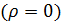 непроводящей
непроводящей 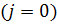 среде с постоянными проницаемостями
среде с постоянными проницаемостями 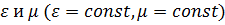 .
.
Тогда уравнения Максвелла принимают вид:
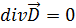
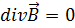
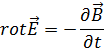
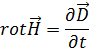
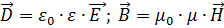
Направим ось x перпендикулярно к волновым поверхностям.
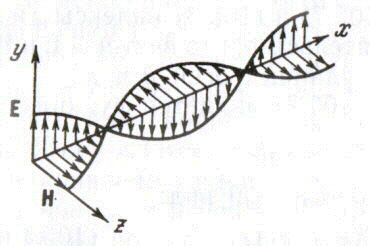
Векторы 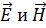 и их компоненты по осям зависят от одной координаты (х) и от времени (t). Тогда уравнения для
и их компоненты по осям зависят от одной координаты (х) и от времени (t). Тогда уравнения для 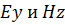 имеют вид:
имеют вид:
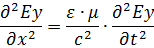
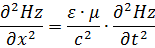
Решения этих уравнений – уравнения электромагнитной волны: