Работа 8. определение постоянной ридберга с помощью универсального монохроматора
Цель работы:
Изучить корпускулярные и волновые свойства частиц, участвующих в процессе перехода атома водорода из возбужденного состояния в стационарное.
Теоретическое введение: некоторые сведения о свойствах атома водорода и его спектра по модели Бора
По упрощенной модели атома Резерфорда- Бора атом состоит из положительно заряженного ядра с зарядом 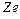 (
( 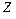 -атомный номер), вокруг которого по круговым орбитам движутся электроны. Каждый из электронов несет отрицательный заряд
-атомный номер), вокруг которого по круговым орбитам движутся электроны. Каждый из электронов несет отрицательный заряд 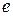 =1,6∙10-19Кл. Для движения по окружности электрон должен обладать центростремительным ускорением. Это ускорение электрону сообщает кулоновская сила взаимодействия электрона с ядром
=1,6∙10-19Кл. Для движения по окружности электрон должен обладать центростремительным ускорением. Это ускорение электрону сообщает кулоновская сила взаимодействия электрона с ядром
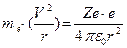 (8.1)
(8.1)
Здесь 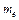 =9,1∙10-31 кг- масса электрона,
=9,1∙10-31 кг- масса электрона, 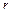 - радиус орбиты,
- радиус орбиты, 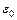 =8,85·10-12Ф/м- электрическая постоянная,
=8,85·10-12Ф/м- электрическая постоянная, 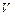 -скорость электрона.
-скорость электрона.
Однако ускоренное движение заряженной частицы есть переменный ток (постоянный ток - это равномерное и прямолинейное движение зарядов), переменный ток создает в пространстве переменное электрическое поле, на которое должна расходоваться энергия электрона.
По этой причине, с классической точки зрения, энергия электрона на орбите должна уменьшаться и он, в конце концов, должен упасть на ядро.
В действительности этого не происходит. Чтобы согласовать этот факт (и другие, необъяснимые с классических позиций, факты) с теорией, Бор ввел следующие, экспериментально подтвержденные, постулаты(-суждения, принимаемые без доказательств):
1. Условие стационарности. Электрон в атоме может находиться только в некоторых определенных устойчивых состояниях, которые называются стационарными.
Находясь в стационарном состоянии электрон не излучает.
2. Условие квантования. Из всех возможных состояний в атоме реализуются только те, для которых момент импульса электрона на орбите (орбитальный момент) равен целому числу постоянных Планка, деленных на 2π
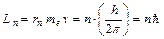 (8.2)
(8.2)
где 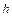 =6,625·10-34 Дж·с,
=6,625·10-34 Дж·с, 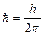 =1,054·10-34 Дж·с,
=1,054·10-34 Дж·с, 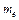 = 9,1∙10-31 кг – масса электрона.
= 9,1∙10-31 кг – масса электрона.
Заметим, что при выполнении этого условия длина орбиты оказывается равной
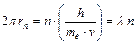 ;
; 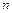 =1,2,3,… (8.3)
=1,2,3,… (8.3)
Это означает, что вдоль боровской орбиты укладывается целое число длин волн электрона (волн де Бройля).
Примечание: волна де Бройля, не является электромагнитной волной и не имеет аналога среди всех видов волн, изучаемых в классической физике. Таким образом, получаются как бы стоячие волны.
Постулаты Бора позволяют сформулировать следующие условия:
1. Условие частот. Атом излучает только при переходе из одного дискретного состояния в другое.
Если обозначить энергию атома в начальном состоянии через 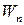 , а в конечном состоянии – через
, а в конечном состоянии – через 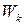 , то разность энергий начального и конечного состояния будет излучена в виде фотона с частотой
, то разность энергий начального и конечного состояния будет излучена в виде фотона с частотой 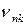 , с энергий
, с энергий 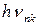 :
:
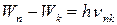 (8.4)
(8.4)
2. Радиусы стационарных орбит. Из формул (8.1) и(8.2) следует:
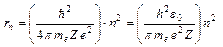 ;
; 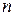 =1,2,3,… (8.5),
=1,2,3,… (8.5),
То есть радиусы орбит пропорциональны квадрату целого числа 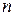 и могут принимать лишь избранные значения, каждое из которых соответствует определенному значению
и могут принимать лишь избранные значения, каждое из которых соответствует определенному значению 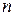 . Радиусы орбит квантованы.
. Радиусы орбит квантованы.
3. Энергия электрона в атоме. Полная энергия электрона в атоме есть сумма кинетической энергии 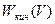 движения на орбите и потенциальной энергии
движения на орбите и потенциальной энергии 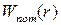 кулоновской силы притяжения к ядру. Потенциальная энергия электрона с зарядом
кулоновской силы притяжения к ядру. Потенциальная энергия электрона с зарядом 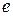 в поле ядра с зарядом
в поле ядра с зарядом 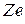 «отрицательна» (состояние электрона связанное) и ее значение в точке, находящейся на расстоянии
«отрицательна» (состояние электрона связанное) и ее значение в точке, находящейся на расстоянии 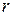 от ядра,
от ядра,
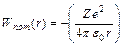 (8.6)
(8.6)
Кинетическая энергия электрона на орбите согласно (8.1):
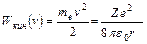 (8.7)
(8.7)
Полная энергия электрона на 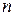 орбите
орбите
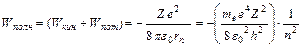 (8.8)
(8.8)
То есть она принимает только некоторые разрешенные значения, зависящие от целого числа 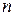 (
( 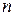 =1,2,3,… ). Таким образом, энергия электрона в атоме квантована. С ростом
=1,2,3,… ). Таким образом, энергия электрона в атоме квантована. С ростом 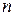 энергия растет (ее абсолютное значение уменьшается). На большом расстоянии от ядра (математически, при
энергия растет (ее абсолютное значение уменьшается). На большом расстоянии от ядра (математически, при 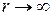 )энергия становится равной нулю и электрон может уйти из атома. Это процесс называется ионизацией атома. Для ионизации атома электрону нужно сообщить энергию, равную полной «отрицательной» энергии в атоме
)энергия становится равной нулю и электрон может уйти из атома. Это процесс называется ионизацией атома. Для ионизации атома электрону нужно сообщить энергию, равную полной «отрицательной» энергии в атоме
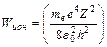 (8. 9)
(8. 9)
4. Возбужденные атомы. В стабильных атомах электрон находится в наинизших энергетических состояниях.
Если атому сообщить энергию, то электрон, приобретая добавочную энергию, переходит на более удаленную от ядра орбиту. Такое состояние атома называется возбужденным.
Через малый промежуток времени ~10-8с атом спонтанно возвращается в основное стабильное состояние, излучая при этом фотон (частицу электромагнитного поля с энергией 
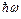 ).
).
5. Спектр атома водорода ( 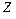 =1)
=1)
Совокупность энергетических уровней атома называется его энергетическим спектром. Если атом водорода переходит из 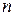 -го состояния, характеризуемого энергией
-го состояния, характеризуемого энергией 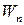 в
в 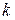 -тое состояние (
-тое состояние ( 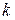 <
< 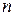 ), характеризуемое энергией
), характеризуемое энергией 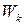 , то при этом излучается фотон с энергией
, то при этом излучается фотон с энергией
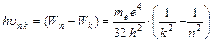 (8.10)
(8.10)
Так как энергия излучаемого кванта зависит от целых чисел 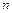 и
и 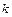 , спектр атома водорода будет состоять из отдельных линий, каждая из которых отвечает определенной длине волны
, спектр атома водорода будет состоять из отдельных линий, каждая из которых отвечает определенной длине волны 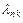 (или частоте
(или частоте 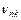 ) излучения.
) излучения.
В спектроскопии принято характеризовать излучение волновыми числами 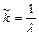 . Волновое число
. Волновое число 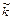 показывает, сколько длин волн укладывается на отрезке длиной 1м, и измеряется в м-1.
показывает, сколько длин волн укладывается на отрезке длиной 1м, и измеряется в м-1.
Из этого определения вытекает, что
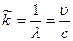 (8.11),
(8.11),
где 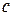 =3·108 м/с- скорость света в вакууме.
=3·108 м/с- скорость света в вакууме.
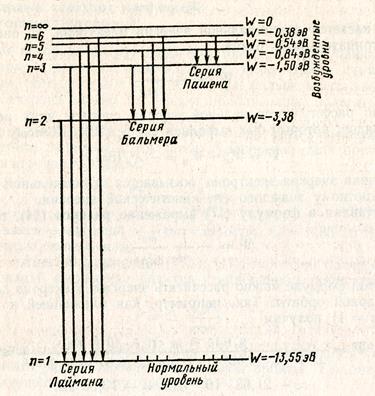
Рис. 8.1
С помощью волновых чисел формулу (8.10) можно представить в виде
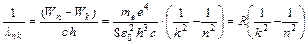 (8.12)
(8.12)
Эта формула называется формулой Бальмера- Ридберга. Множитель перед скобкой называется постоянной Ридберга, обозначается 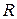 =1,1·107м-1.
=1,1·107м-1.
Формула (8.12), полученная из закона сохранения энергии, хорошо описывает все линии спектра водорода.
При переходе с внешних орбит на первую орбиту ( 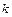 =1,
=1, 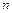 =2,3,4,… ) получается серия Лаймана. При переходах на вторую орбиту (
=2,3,4,… ) получается серия Лаймана. При переходах на вторую орбиту ( 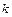 =2,
=2, 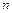 =3,4,5,…)получается серия Бальмера, при переходах на третью орбиту (
=3,4,5,…)получается серия Бальмера, при переходах на третью орбиту ( 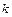 =3,
=3, 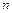 =3,4,5, … ) – серия Пашена и др.(см. справочную таблицу 8.1 и рис.8.1).
=3,4,5, … ) – серия Пашена и др.(см. справочную таблицу 8.1 и рис.8.1).
Таблица 8.1. Спектр атома водорода
 | 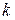 | серия | Область спектра | Длина волны 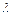 ,нм ,нм |
| Лаймана | ультрафиолетовая | |||
| Бальмера | видимая | |||
| Пашена | инфракрасная | |||
| Бреккета | инфракрасная | |||
| Пфунда | инфракрасная | |||
Описание установки
В работе постоянная Ридберга 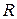 определяется на основе формулы (8.12) измерением длин волн видимой части водородного спектра, т. е. линий спектра, принадлежащих серии Бальмера (
определяется на основе формулы (8.12) измерением длин волн видимой части водородного спектра, т. е. линий спектра, принадлежащих серии Бальмера ( 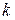 =2,
=2, 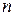 =3,4,5,… ).
=3,4,5,… ).
Для измерения длин волн в работе используется монохроматор УМ-2 –спектрометр, предназначенный для различного рода спектральных исследований. Оптическая схема монохроматора приведена на рис.8.2.
Рис.8.2
1-источник света
2-входная щель
3-диспергирующая призма
4-визирный указатель
5-окуляр
Свет от источника 1 через входную щель 2 падает на диспергирующую призму 3. Данная призма является главной частью прибора. Она установлена на призменном столике с поворотным механизмом. Назначение призмы – разлагать свет исследуемого источника на составляющие монохроматические лучи. С помощью поворотного механизма призма поворачивается на разные углы, в результате чего в окуляре 5 просматриваются различные спектральные линии. Барабан поворотного механизма проградуирован в градусах. Для отсчета имеется указатель шкалы.
Выходная труба содержит объектив, фокусирующий параллельные лучи в фокальной плоскости окуляра 5. в этой же плоскости находится визирный указатель 4. В процессе работы этот указатель должен быть подведен к центру измеряемой спектральной линии. Ширина и интенсивность последней определяется шириной раскрытия входной щели 2, которая регулируется с помощью специального винта на приборе. В качестве источника света в работе используется газоразрядная трубка с водородом. Для определения постоянной Ридберга в работе измеряются длины волн трех линий водородного спектра – красной линии (  =2,
=2,  =3), голубой линии (
=3), голубой линии ( 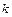 =2,
=2, 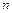 =4) и фиолетовой линии(
=4) и фиолетовой линии( 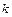 =2,
=2, 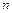 =6) . Для нахождения длины волны измеряемой линии по найденному отсчету по шкале барабана используют градуировочную кривую монохроматора, которая находится около установки.
=6) . Для нахождения длины волны измеряемой линии по найденному отсчету по шкале барабана используют градуировочную кривую монохроматора, которая находится около установки.
Порядок выполнения работы
1. Включить водородную трубку, просмотреть, вращая барабан, весь спектр.
2. Совместить визирный указатель с центром красной линии и снять отсчет по барабану –N. Используя градуировочную кривую, определить длину волны 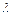 красной линии.
красной линии.
3. Определить длину волны голубой линии, выполнив измерения согласно пункту 3.
4. Определить длину волны фиолетовой линии, выполнив измерения согласно пункту 3.
5. Полученные результаты занести в таблицу 8.2
| № п/п | Цвет линии | N, град | 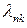 ,м ,м | Ri, м-1 | R ср, м-1 | ΔRi, м-1 | ΔRср, м-1 | δR= 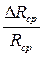 ,% ,% |
| красный | ||||||||
| голубой | ||||||||
| фиолетовый |
6. Подставляя в формулу (8.12) найденные из опыта 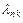 и соответствующие значения
и соответствующие значения 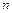 и
и 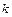 , вычислить постоянную Ридберга Ri (i=1,2) по каждой линии. Найти среднее значение
, вычислить постоянную Ридберга Ri (i=1,2) по каждой линии. Найти среднее значение 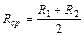 и сравнить его с табличным
и сравнить его с табличным 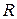 =1,1·107м-1.
=1,1·107м-1.
7. Вычислить абсолютную ΔRср и относительную δR погрешности и записать окончательный результат определения постоянной Ридберга, полученной в результате проведенного эксперимента.
8. Рассчитать энергию ионизации атома водорода по формуле(9) и выразить ее в электронвольтах (1эВ=1,6∙10-19Дж).
Таблица 8.2
9. Рассчитать боровский радиус (радиус первой ( 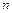 =1) орбиты атома водорода), используя формулу (8.5).
=1) орбиты атома водорода), используя формулу (8.5).
Контрольные вопросы
1. Что называется спектром атома водорода?
2. Какое состояние атома называется возбужденным?
3. Из какого условия определяется энергия фотона при переходе из 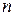 состояния атома в
состояния атома в 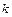 (
( 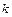 <
< 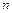 )?
)?
4. Из какого условия определяется длина волны излучения при переходе электрона с 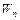 на
на 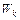 (взять
(взять 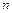 =3,
=3, 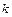 =2)?
=2)?
5. Какой процесс называется ионизацией атома? Записать определение энергии ионизации, указать единицы измерения физических величин, определяющих 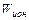 .
.
6. Дать определения спонтанных и вынужденных процессов в атоме водорода.
7. Что называется фотоном и каковы его физические характеристики?
8. Кинетическая, потенциальная и полная энергии электрона в атоме водорода?
9. Сформулируйте условие частот.
10. Чем обусловлен дискретный характер состояний атома водорода.
11. Сформулируйте постулаты Бора.
12. Запишите условие квантования момента импульса.
13. Запишите условие для определения радиусов стационарных орбит.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ К РАБОТАМ 9,10 и 11
Наряду с волновыми свойствами свету присущи также и корпускулярные (квантовые) свойства, на основе которых находит объяснение, в частности, такое явление, как фотоэлектрический эффект. Фотоэффектом называется освобождение (полное или частичное) электронов от связей с атомами и молекулами вещества под действием света. Если электроны выходят за пределы освещаемого вещества (полное освобождение), то фотоэффект называется внешним.
Теория фотоэффекта разработана А.Эйнштейном. В основу теории положены квантовые представления о природе света, согласно которым излучение, распространение и поглощение света происходит порциями - квантами (фотонами).
Энергия кванта определяется формулой Планка
W = h·ν (9.1)
где ν – частота излучения, h = 6,625·10-34Дж·с – постоянная Планка.
Для внешнего фотоэффекта выполняется закон Эйнштейна:
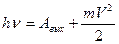 (9.2)
(9.2)
где Авых – работа выхода электрона из металла, 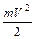 - кинетическая энергия освободившегося электрона, hν – энергия падающего кванта света. Уравнение (9.2) дает теоретическое обоснование экспериментальных законов фотоэффекта.
- кинетическая энергия освободившегося электрона, hν – энергия падающего кванта света. Уравнение (9.2) дает теоретическое обоснование экспериментальных законов фотоэффекта.
1). Первый закон фотоэффекта (закон Столетова). Световой поток, т.е. световая энергия, излучаемая в единицу времени, согласно квантовой теории определяется числом квантов. Каждый квант, падающий на поверхность металла, взаимодействует только с одним электроном, поэтомуфототок насыщения (максимальное число фотоэлектронов, испускаемых металлом в единицу времени) должен быть пропорционален падающему световому потоку:
Iнас = kФ (9.3)
где k – коэффициент пропорциональности или фоточувствительность катода.
2).Второй закон фотоэффекта.Из уравнения (9.2) следует, что с ростом частоты падающего света ν возрастает кинетическая энергия выбитых электронов, т.к. Авых = const для данного металла. Следовательно,кинетическая энергия фотоэлектронов зависит лишь от частоты падающего света.
3). Третий закон фотоэффекта.При частоте падающего света ν = ν0, при которой
h·ν0 = Авых (9.4)
кинетическая энергия электрона равна 0. При меньших частотах излучения фотоэффект наблюдаться не будет. Частота ν0 или соответствующая ей длина волны 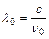 называется красной границей фотоэффекта.
называется красной границей фотоэффекта.
Согласно (9.4), красная граница 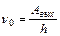 зависит, как и работа выхода, лишь от материала фотокатода. Для каждого материала существует красная граница, т.е. минимальная частота излучения ν0, при которой еще существует фотоэффект.
зависит, как и работа выхода, лишь от материала фотокатода. Для каждого материала существует красная граница, т.е. минимальная частота излучения ν0, при которой еще существует фотоэффект.
Внутренним фотоэффектомназывается явление образования добавочных свободных носителей тока в полупроводнике под действием падающего на него света. Добавочную проводимость, обусловленную внутренним фотоэффектом, называют фотопроводимостью. Полупроводниковый прибор, в котором используется явление внутреннего фотоэффекта, называют фоторезистором. Сопротивление фоторезистора при освещении светом уменьшается.
В случае чистых полупроводников электронная и дырочная фотопроводимости одинаковы и малы. В примесных полупроводниках n – типа наблюдается в основном электронная фотопроводимость, а в полупроводниках р - типа наблюдается дырочная фотопроводимость. Электронная фотопроводимость определяется по формуле
γ = nтeU+nфeU, (9.5)
где e- заряд электрона, nт – концентрация свободных электронов в затемненном фоторезисторе, nф – концентрация свободных электронов, появившихся в полупроводнике в результате облучения его светом, U – подвижность электронов. Таким образом, первое слагаемое в (9.5) отвечает темновой проводимости и обуславливает темновой ток Iт, а второе слагаемое – фотопроводимости, которая обуславливает фототок Iф.
Явления внешнего и внутреннего фотоэффекта находят широкое практическое применение.
