Теория сигналов. Классификация. Основные характеристики сигналов

Лекция №2 Радиотехнические сигналы

Изменение во времени напряжения, тока, заряда или мощности в электрических цепях называют электрическим колебанием. Используемое для передачи информации электрическое колебание является сигналом. Сложность процессов в электрических цепях зависит от сложности исходных сигналов. Поэтому целесообразно пользоваться спектром сигналов. Из математики известны ряды и преобразования Фурье, с помощью которых удается представить сигналы совокупностью гармонических составляющих. На практике полезен анализ характеристики, дающий представление о скорости изменения и длительности сигнала. Это удается достичь с помощью корреляционного анализа.

2.1. Общие сведения о радиотехнических сигналах

Традиционно радиотехническими принято считать электрические (а теперь и оптические) сигналы, относящиеся к радиодиапазону. С математической точки зрения всякий радиотехнический сигнал можно представить некоторой

функцией времени u(t), которая характеризует изменение его мгновенных значений напряжения (такое представление применяют чаще всего), тока, заряда или мощности. Каждый класс сигналов имеет свои особенности и требует специфических методов описания и анализа. Одним из ключевых компонентов представления и обработки сигналов является анализ. Основной целью анализа служит сравнение сигналов друг с другом для выявления их сходства и различия. Различают три основные составляющие анализа электрических сигналов:

• измерение числовых параметров сигналов (энергию, среднюю мощность и среднее квадратическое значение);

• разложение сигнала на элементарные составляющие либо для их рассмотрения по отдельности, либо для сравнения свойств различных сигналов; такое разложение проводят с использованием рядов и интегральных преобразований, важнейшими из которых являются ряды и преобразование Фурье;

• количественное измерение степени «похожести» различных сигналов, их параметров и характеристик; такое измерение производят с применением аппарата корреляционного анализа.

Для того чтобы сделать сигналы объектами изучения и расчетов, следует указать способ их математического описания, т. е. создать математическую модель исследуемого сигнала. В радиотехнике каждому классу сигналов соответствует свое математическое представление, своя математическая модель, причем одна и та же математическая модель может практически всегда адекватно описывать напряжение, ток, заряд, мощность, напряженность электромагнитного поля и т. д. Наиболее распространенными способами представлений (описаний) сигналов являются временной, спектральный, аналитический, статистический, векторный, графический и геометрический. Функции, описывающие сигналы, могут принимать как вещественные, так и комплексные значения. Поэтому в дальнейшем в книге часто будем говорить о вещественных и комплексных сигналах.Часть краткой классификации сигналов по ряду признаков приведена на рис.2.1.

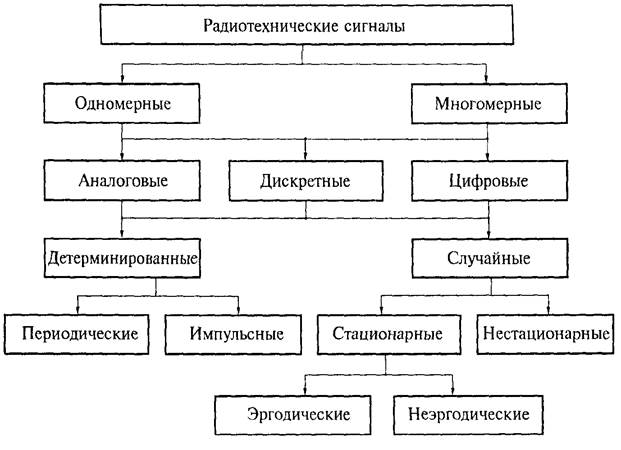Рис.2.1. Классификация радиотехнических сигналов

Радиотехнические сигналы удобно рассматривать в виде математических функций, заданных во времени и физических координатах. С этой точки зрения сигналы обычно описывается одной (одномерный сигнал; п = 1), двумя (двумерный сигнал; п = 2) или более (многомерный сигнал п > 2) независимыми переменными. Одномерные сигналы являются функциями только времени, а многомерные, кроме того, отражают положение в «-мерном пространстве.Будем для определенности и упрощения в основном рассматривать одномерные сигналы, зависящие от времени,многомерный случай, когда сигнал представляется в виде конечной или бесконечной совокупности точек, например в пространстве, положение которых зависит от времени. В телевизионных системах сигнал черно-белого изображения можно рассматривать как функцию f(x,у,f) двух пространственных координат и времени, представляющую интенсивность излучения в точке (х, у) в момент времени t на катоде. При передаче цветного телевизионного сигнала имеем три функции f(x, у, t), g(x, у, t), h(x, у, t), определенные на трехмерном множестве (можно рассматривать эти три функции также как компоненты трехмерного векторного поля). Кроме того, различные виды телевизионных сигналов могут возникать при передаче телевизионного изображения совместно со звуком.Многомерный сигнал — упорядоченная совокупность одномерных сигналов. Многомерный сигнал создает, например, система напряжений на зажимах многополюсника (рис. 2.2).

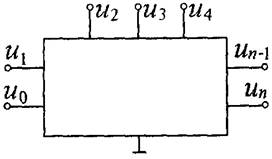
Рис. 2.2. Система напряжений многополюсника.

Многомерные сигналы описывают сложными функциями, и их обработка чаще возможна в цифровой форме. Поэтому многомерные модели сигналов особенно полезны в случаях, когда функционирование сложных систем анализируется с помощью компьютеров. Итак, многомерные, или векторные, сигналы состоят из множества одномерных сигналов

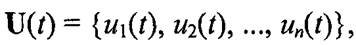
где n— целое число, размерность сигнала. По особенностям структуры временного представления (рис. 2.3) все радиотехнические сигналы делятся на аналоговые (analog), дискретные (discrete-time; от лат.discretus— разделенный, прерывистый) и цифровые (digital). Если физический процесс, порождающий одномерный сигнал, можно представить непрерывной функцией времени u(t) (рис. 2.3, а), то такой сигнал называют аналоговым (непрерывным). Примером аналогового сигнала является некоторое напряжение, которое подано на вход осциллографа, в результате чего на экране возникает непрерывная кривая как функция времени. Дискретный сигнал получают из аналогового путем специального преобразования. Процесс преобразования аналогового сигнала в последовательность отсчетов называется дискретизацией (sampling), а результат такого преобразования — дискретным сигналом или дискретным рядом (discrete series). Простейшая математическая модель дискретного сигнала Un(t) — последовательность точек на временной оси, взятых, как правило, через равные промежутки времени Т = ∆t, называемые периодом дискретизации (или интервалом, шагом дискретизации; sample time), и в каждой из которых заданы значения соответствующего непрерывного сигнала (рис. 2.3, б). Величина, обратная периоду дискретизации, называется частотой дискретизации (sampling frequency):f_Д= 1/Т (другое обозначениеf_Дf_Д= 1/∆t). Соответствующая ей угловая (круговая) частота определяется следующим образом: ω_Д= 2π /∆t.

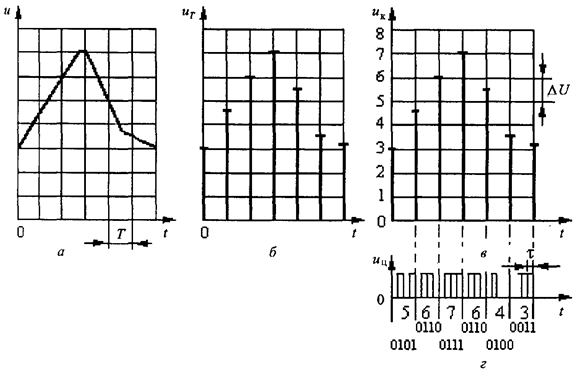
Рис. 2.3. Радиотехнические сигналы: а — аналоговый; б — дискретный; в — квантованный; г — цифровой

Разновидностью дискретных сигналов является цифровой сигнал (digital signal), В процессе преобразования дискретных отсчетов сигнала в цифровую форму (обычно в двоичные числа) производится его квантование по уровню (quantization) напряжения ∆. При этом значения уровней сигнала можно пронумеровать двоичными числами с конечным, требуемым числом разрядов. Сигнал, дискретный во времени и квантованный по уровню, называют цифровым сигналом.В цифровом сигнале дискретные значения сигнала u_T(t) вначале квантуют по уровню (рис. 2.3, в) и затем квантованные отсчеты дискретного сигнала заменяют числами u_Ц(t), чаще всего реализованными в двоичном коде, который представляют высоким (единица) и низким (нуль) уровнями потенциалов напряжения — короткими импульсами длительностью τ (рис. 2.3, г). Такой код называют униполярным. При представлении сигнала неизбежно происходит его округление. Возникающие при этом ошибки округления называются ошибками (или шумами) квантования (quantization error, quantization noise). Последовательность чисел, представляющая сигнал при цифровой обработке, является дискретным рядом (discrete series). Одним из основных признаков, по которым различаются сигналы, является предсказуемость сигнала (его значений) во времени.Детерминированными называют радиотехнические сигналы, мгновенные значения которых в любой момент времени достоверно известны.Простейшими примерами детерминированного сигнала являются гармоническое колебание с известной начальной фазой, высокочастотные колебания, модулированные по известному закону. Детерминированный сигнал не может быть носителем информации.Детерминированные сигналы разделяют на периодические и непериодические (импульсные). Сигнал конечной энергии, существенно отличный от нуля в течение ограниченного интервала времени, соизмеримого со временем завершения переходного процесса в системе, для воздействия на которую он предназначен, называют импульсным сигналом.

Случайными называют сигналы, мгновенные значения которых в любой момент времени не известны и не могут быть предсказаны с вероятностью, равной единице. Сигналом, несущим полезную информацию, может быть только случайный сигнал.

Случайные процессы, параметры и свойства которых можно определять по одной случайной реализации (выборке) называются эргодическими, они обладают определенными свойствами.

Часто при описании и анализе некоторых видов сигналов (в первую очередь узкополосных) бывает удобной комплексная форма их представления

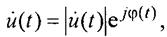
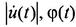где -соответственно модуль и фаза комплексной величины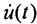

Комплексная функция u(t) может быть также представлена в виде

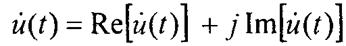
где Re, Im — действительная и мнимая части комплексной функции. Из обоих формул получим:

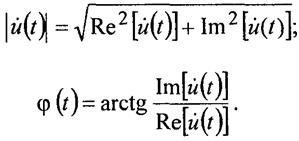
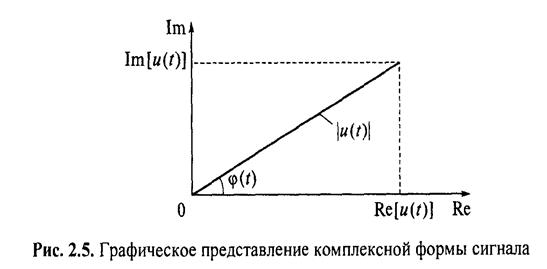
При векторном представлении комплексный сигнал — это вектор на комплексной плоскости с действительной осью — осью абсцисс и мнимой осью — осью ординат (рис. 2.5). Вектор на плоскости вращается в положительном направлении (против часовой стрелки) со скоростью ω₀. Длина вектора равна модулю комплексного сигнала, угол между вектором и осью абсцисс — аргументу φ₀. Проекции вектора на оси координат равны соответственно действительной и мнимой частям комплексной величины.