Електричний струм у різних середовищах

Густина струму в металі:

,

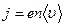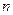де − заряд електрона, − концентрація вільних електронів (тобто число їх в одиниці об'єму), 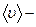середня швидкість напрямленого руху електронів.

Густина струму в газі при відсутності насичення:

,

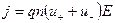де 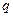− абсолютне значення заряду кожного іона, 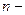концентрація іонів одного знаку в одиниці об'єму), 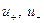− рухливість позитивних і негативних іонів, 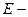напруженість електричного поля в газі.

Густина струму насичення в газі між плоскими електродами, відстань між якими 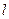, дорівнює:

,

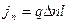де 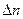− число пар іонів, щомиті утворених іонізатором в одиниці об'єму газу.

Електрон може залишити метал лише за умови, що його кінетична енергія:

,

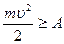де 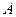− робота виходу електрона з даного металу.

Густина струму насичення при термоелектронній емісії (питома емісія) визначається формулою:

,

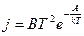де 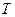– абсолютна температура металу, 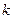– стала Больцмана, 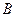– постійна, різна для різних металів.

Питома електропровідність електроліту:

,

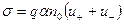де 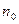− концентрація молекул розчиненої речовини, 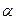− коефіцієнт дисоціації, рівний відношенню числа дисоційованих молекул до їх загального числа.

Для електричного струму в електроліті мають місце два закони Фарадея:

1) маса 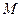речовини, що виділяється при електролізі, дорівнює:

,

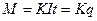де 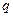− кількість електрики, що пройшла через електроліт, 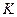− електрохімічний еквівалент;

2) електрохімічний еквівалент пропорційний хімічному еквіваленту, тобто:

,

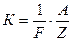де 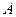− маса одного кг-атома, 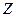–валентність, 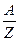− маса кг-еквівалента, і 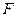− число Фарадея, чисельно рівне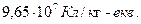

Магнітне поле

Магнітне поле струму

За законом Біо-Савара-Лапласа елемент контуру 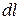, по якому протікає струм 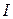, створює в деякій точці 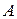простору магнітне поле напруженістю :

,

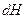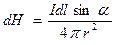де 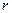– відстань від елементу струму 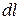до точки 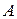, 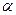– кут між радіус-вектором 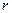і елементом струму 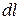. Застосовуючи закон Біо-Савара-Лапласа до контурів різних видів, можна знайти:

– напруженість магнітного поля, створеного нескінченно довгим прямолінійним провідником із струмом:

,

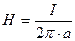де 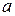– відстань від точки, де визначається напруженість, до провідника зі струмом;

– напруженість магнітного поля на осі колового струму:

,

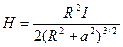де 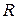– радіус колового контуру зі струмом, 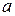– відстань від точки, де визначається напруженість, до площини контуру;

– напруженість магнітного поля всередині тороїду та нескінченно довгого соленоїду:

,

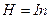де 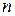– число витків, що припадають на одиницю довжини соленоїда (тороїда);

– напруженість магнітного поля на осі соленоїда скінченої довжини:

,

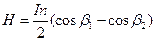де 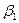і 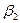– кути між віссю соленоїда і радіус-вектором, проведеним із розглядуваної точки до кінців соленоїда.

Магнітна індукція 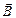пов’язана з напруженістю 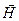магнітного поля співвідношенням:

,

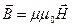де 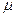– відносна магнітна проникність середовища і 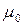– магнітна стала, рівна

.

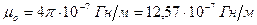Об’ємна густина енергії магнітного поля рівна:

.

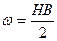Потік магнітної індукції через контур дорівнює:

,

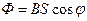де 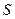– площа поперечного перерізу контура, 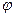– кут між нормаллю до площини контура і напрямом магнітного поля.

На елемент 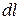провідника зі струмом, що знаходиться в магнітному полі індукцією 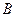, діє сила Ампера:

,

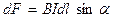де 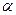– кут між напрямом струму та напрямом магнітного поля.

Сила, що діє на заряджену частинку, що рухається зі швидкістю 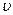в магнітному полі, визначається формулою Лоренца:

,

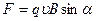де 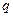– заряд частинки, 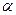– кут між напрямом швидкості частинки і напрямом магнітного поля.

Магнітний момент контуру зі струмом:

,

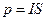де 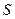– площа контура.

Робота переміщення провідника зі струмом в магнітному полі:

,

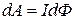де 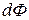– потік магнітної індукції, який перетинає при своєму русі провідник.

Електромагнітна індукція

Явище електромагнітної індукції полягає у виникненні в контурі е.р.с. індукції при зміні потоку магнітної індукції 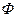крізь поверхню, що охоплює контур. Величина е.р.с. індукції визначається рівнянням:

.

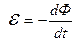Зміна потоку магнітної індукції може досягатися зміною сили струму в самому контурі (явище самоіндукції). При цьому е.р.с. самоіндукції визначається формулою:

,

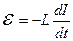де 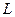– індуктивність (коефіцієнт самоіндукції) контуру.

Індуктивність соленоїда:

,

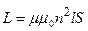де 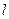– довжина соленоїда, 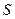– площа його поперечного перерізу, 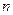– число витків, що припадають на одиницю його довжини.

Внаслідок явища самоіндукції сила струму в колі при вимкненні е.р.с. спадає за законом:

,

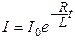а при вмиканні е.р.с. сила струму зростає за законом:

,

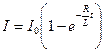де 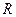– опір кола.

Магнітна енергія контуру з струмом дорівнює:

.

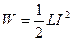Кількість заряду, що проходить через поперечний переріз провідника при виникненні в ньому індукційного струму, дорівнює:

.
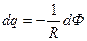