Розподіл Максвелла молекул за швидкостями. Найбільш імовірна швидкість молекул. Середня і середньоквадра-тична швидкості молекул

В розподілі Максвелла частинок за кінетичними енергіями (2.2.10) виразимо р і e через швидкості газових молекул 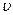, а також визначимо нормувальний коефіцієнт А₂.

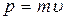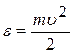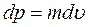Оскільки , і , то

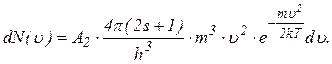(2.2.13)

Проінтегруємо цей вираз в межах зміни 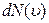від 0 до N, а зміни швидкості від 0 до ∞, одержимо:

.

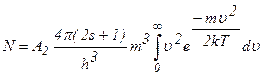Інтеграл 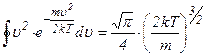, тому

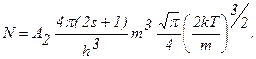(2.2.14)

З цього виразу визначимо нормувальний коефіцієнт А₂, тобто

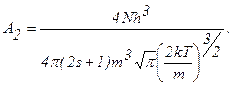
Підставимо значення цього коефіцієнта в (2.2.13), одержимо

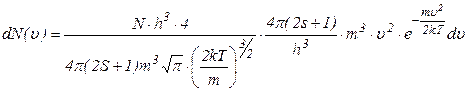, (2.2.15)

Після відповідного скорочення та незначного перетворення одер-жимо розподіл Максвелла молекул за швидкостями

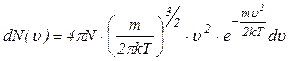. (2.2.16)

Фізично розподіл Максвелла визначає частку молекул 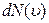від загального числа молекул 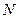швидкості яких перебувають в межах значень від 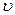до 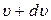. Графічно розподіл Максвелла газових молекул за швидкостями має вигляд, показаний на рис.2.6.

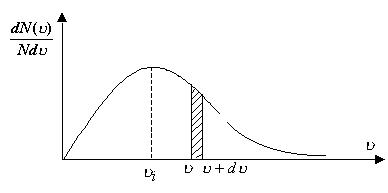
Рис. 2.6

Залежність 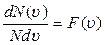носить назву функції розподілу Максвелла. Власне на рис. 2.6 показаний графік залежності функції розподілу Максвелла від швидкості газових молекул, тобто .

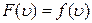Заштрихована частина під розподілом Максвелла визначає величину імовірності числа частинок системи, швидкості яких перебувають у межах від 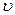до 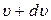. Зрозуміло, що вся площа під розподілом Максвелла відповідає імовірності, рівній одиниці.

Дослідимо функцію розподілу Максвелла на максимум. Для цього похідну функції Максвелла за швидкостями прирівняємо до нуля

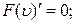або 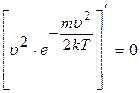, звідки

.

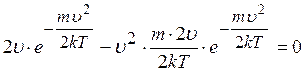Після скорочення одержуємо найбільш імовірну швидкість

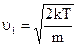. (2.2.17)

Швидкість (2.2.17) означає, що більшість молекул газової системи мають саме таку швидкість. На рис 2.6 ця швидкість характеризує пік роз-поділу.

Для визначення середньої швидкості газових молекул слід скориста-тися формулою (2.1.6). Середня швидкість газових молекул у відповідно-сті з цією формулою буде дорівнювати

,

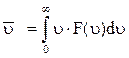або

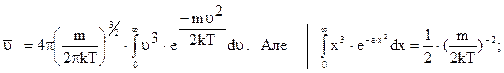
Після відповідних перетворень одержимо середню швидкість молекул:

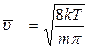. (2.2.18)

Для знаходження середньоквадратичної швидкості виконаємо розрахунок аналогічно формулі (2.1.7)

,

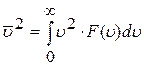або

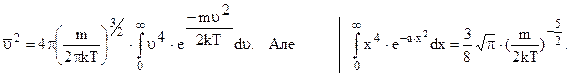
тому

.

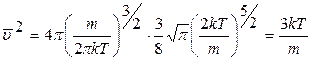Середньоквадратична швидкість молекул газової системи буде дорівнювати

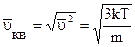. (2.2.19)

З цих міркувань можна зробити висновок, що будь-яку газову сис-тему можна характеризувати трьома різними значеннями швидкостей молекул :

· найбільш імовірна швидкість молекул

;

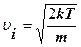· середня швидкість молекул

;

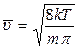· середньоквадратична швидкість молекул

.

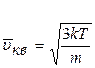Домножимо чисельник і знаменник правої частини кожної із формул швидкостей газових молекул на число Авогадро N_a. З урахуванням того, що 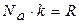і 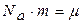, одержимо :

;

;

,

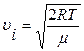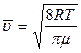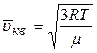де m ― маса однієї молекули; к ― стала Больцмана; Т ― абсолютна температура; R ― газова стала; 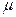― молярна маса газу.

Лекція 3. Молекулярна фізика й термодинаміка