Дәріс. Тікбұрышты металл толқынжол

Тікбұрышты металл толқынжол – бұл көлденең қимасы тікбұрышты болып келетін идеалды өткізгіш ( 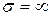) металл түтік (5.1.суретте).

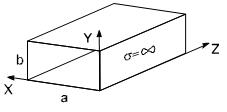
5.1.сурет – тікбұрышты металл толқынжол

Толқынжол 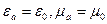параметрлеріне ие (ауа) затпен толтырылған деп қарастырайық. Толқынжолдың ішінде бүкіл ось бойына Н-типті толқын бар болсын дейік:

Осы толқындар мына сипатқа ие .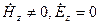

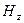функциясы Гельмгольц теңдеулерінің шешімі болып табылады:

,

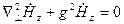мұндағы 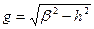– көлденең толқындық сан.

Гельмгольц теңдеулерін шешу кезінде шекаралық шарттарға назар аудару керек (Е-нің тангенциальды құраушылары о- ге тең):

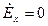болғанда y = 0, y = b;

болғанда x = 0, x = а.

Гельмгольц теңдеуін шеше отырып мынаны аламыз:

.

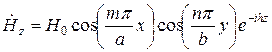Тек мына шарттар орындалғанда ғана теңдеудің шешімі 0-ге тең болмайды:

,

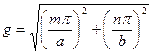мұндағы m және n – кез келген оң, бүтін және 0-ге тең емес сан (басқа жағдайда магниттік өрістің Н күш сызықтары тұйықталмаған және Максвеллдің төртінші теңдеуіне қайшы келеді).

Әрбір g-тің мәніне 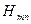толқыны деп аталатын (мұндағы m және n – толқынның индексі) Максвелл теңдеулерінің бірі сәйкес келеді. Оның физикалық мағанасы – толқынжолдың ішінде пайда болатын, координата бойынша х және у осьтеріне сәйкес келетін тұрғын жартытолқындардың санын білдіреді.

Формулаларды ауыстыра отырып ( ), басқа да 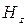проекциялары үшін өрнектер аламыз. Нәтижесінде электромагниттік өрістің 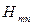типті толқынының құрылымы мына формулалармен сипатталады:

;

; .

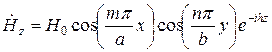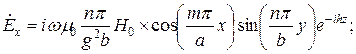
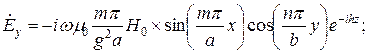
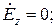
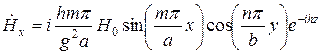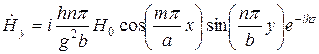Жоғарыда келтірілген формулалар жүйесі 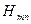типті электромагниттік өріс толқындары туралы исчерпывающую ақпарат береді. Өрістің бейнесі z осі бойымен периодталған; кеңістіктік период ретінде толқынжолдағы толқын ұзындығы қолданылады:

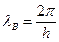. (5.1)

Созылған (продольное) толқындық сан 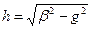толқынжолдың жұмыс істеу аймағын анықтайды. Егер жұмыстық толқын ұзындығы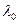 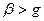болатындай аз болса, онда h нақты болады және электромагниттік тербеліс тұрақты амплитуданың тұрақты толқыны ретінде таралады. Егер 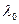-ны 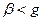болатындай етіп арттырсақ, онда толқынжолда қума толқындардың орнына тек қана таралатын тербеліс қана бола алады. Оның амплитудасы z бойымен экспонента бойынша кемиді, ал фаза болса барлық көлденең қималарда тұрақты – толқынжол отсечки режимінде жұмыс істейді. 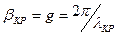жұмыс жиілігі кезінде шекаралық жағдай пайда болады.

Бұл жағдайда h = 0 , 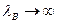, ал генератордың толқын ұзындығын критикалық деп атайды:

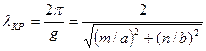. (5.2)

(5.1) өрнегін пайдалана отырып, 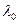-тің 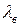-тен тәуелділігін алуға болады:

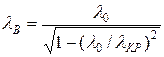, (5.3)

Бұл толқынжолдың дисперсиялық сипаттамасы деп аталады. Бұл сипаттама z-тен тәуелділік exp(-ihz)-пен анықталған кезде ғана орындалады, және отсечки режимінің бар болуы туралы жорамал бойынша бұл тәуелділік кез келген типті және кез келген қимасы бар металл толқынжол үшін орындалады.

Дисперсиялық сипаттамасын бейнелесек (5.2-сурет). Критикалық толқын ұзындығына дейін 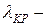мөлдірлілік (прозрачности) аймағы, .

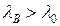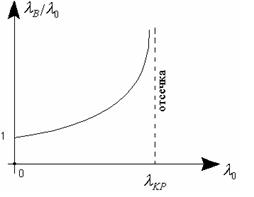
5.2 сурет – толқынжолдың дисперсиялық сипаттамасы

Бұл бөлікте фазалық және топтық жылдамдық мына өрнектермен анықталады:

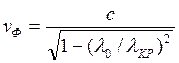; (5.4)

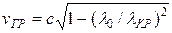. (5.5)

Бұл жерде фазалық жылдамдық әрқашан жарық жылдамдығынан көбірек болады, ал топтық жылдамдық әрқашан жарық жылдамдығынан аз болады. Бұдан шығатыны- кез келген жиілікте 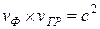орындалады.

Толқыны.

(5.2.) формуласына m = 1 және n = 0 толқын индекстерін қоя отырып, 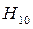толқыны үшін критикалық толқын ұзындығын аламыз:

.

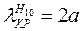Толқынның осы индекстерін өріс толқынының құраушыларына қойып, электромагниттік өрістің құрылымын сипаттаушы формулаларды аламыз:

;

;

;

.

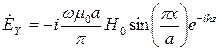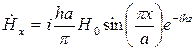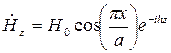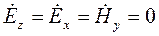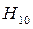типті толқынның құраушыларының максималды мәндерін алып, тәуелділік графигін тұрғызамыз (5.3. сурет).

Өрістің кеңістіктік құрылымын анық көру үшін электр және магнит өрістерінің күш сызықтарының суретін саламыз (5.4.сурет). В поперечном сечении - стоячая волна и эта картина смещается вдоль z с фазовой скоростью.

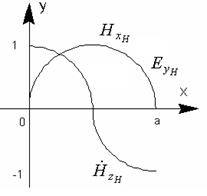
5.3 сурет –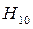типті өріс толқынының құраушыларының нормаланған тәуелділігі.

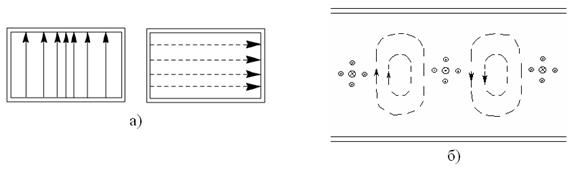
5.4 сурет – электр және магнит өрістерінің күш сызықтарының кеңістіктік құрылымы: а) алдынғы жақтан көрініс; б) жоғарыдан көрініс;

Е үшін орталықта концентрация максималды, ал шеткі бөліктерде 0-ге тең. Н үшін күш сызықтары тұйықталған және у-тан тәуелділік болмайды. 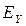және 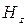максимумдары кеңістікте фаза бойынша 90 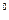-қа жылжыған ( 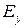және 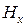сәйкес келеді). Әрбір жарты толқын ұзындығынан кейін бағыт ауысып отырады.

Е тек қана бір құраушыға 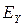ие болғандықтан, Е векторы сызықты полярланған. Ал 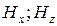жалпы жағдайда Н векторы эллипстік полярланған, бірақ X = 0 , а/2 , а кезінде сызықты полярланған. Ал 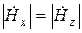шарты орындалғанда Н векторы шеңбер бойынша полярланған ( 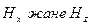әрқашан фаза бойынша 90 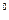-қа жылжыған). Бұл шарт 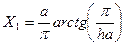және 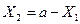кезінде орындалады. Бұл нүктелер орталықпен салыстырғанда симметриялы орналасқан (шеткі бөліктен шамамен а/4 қашықтықта орналасқан).

Өрнектерден өріс құраушылары үшін Пойтинг векторы екі құраушыларға 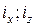ие екені көрінеді, бірақ негізінен өріс тек қана z осі бойынша таралады:

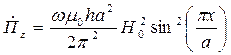
Яғни толқынжолдың орта бөлігінде энергия максимум мәнге ие болады.