Лекция 10. Спонтанное деление ядер. Атомно-молекулярные последствия радиоактивного распада
10.1. Спонтанное деление ядер. Энергия деления. В 1940 г. Г. Флеровым и К. Петржаком было открыто спонтанное (т.е. самопроизвольное) деление ядер урана: распад на два ядра-осколка сравнимой массы. Такое деление, как уже отмечалось (п. 2.3), энергетически выгодно для тяжелых ядер: это следует из зависимости удельной энергии связи W(A, Z)/A от массового числа А. При делении совершается переход к более легким ядрам, в которых нуклоны связаны сильнее, и часть энергии (около 0,9 МэВ/нуклон) высвобождается. Действительно, если разделить ядро с А = 238 (W/A ≈ 7,6 МэВ) на два осколка с одинаковым массовым числом A1 = A2 = A/2 = 119 (W/A ≈ 8,5 МэВ), высвободится энергия
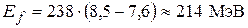 ,
,
т.е. ~ 1014 Дж/кг, что на много порядков превосходит энерговыделение всех других освоенных человеком источников энергии.
Найдем условие, при котором деление ядра (A, Z) будет энергетически выгодным. Для этого выразим энергию деления Ef через энергию связи W(A, Z) материнского ядра и осколков. Так как число протонов Z и число нейтронов A – Z в ходе деления остается постоянным, то
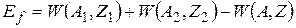 .
.
Будем, как и до этого, рассматривать деление на осколки с одинаковым массовым числом, причем количество протонов в каждом из осколков также будет одинаковым. Это позволяет записать
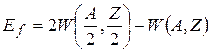 . (10.1)
. (10.1)
Для дальнейшего анализа будем рассматривать ядро в рамках модели жидкой капли и использовать формулу Вайцзеккера для энергии связи. Тогда, пренебрегая незначительной энергией спаривания δА–3/4 и учитывая, что объемная энергия и энергия симметрии не изменяются при делении (так как сумма нуклонов и баланс между протонами и нейтронами одинаковы для материнского ядра и осколков деления), энергию связи можно представить как
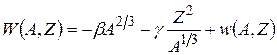 , (10.2)
, (10.2)
где в w(A, Z) входят все слагаемые, за исключением тех, что соответствуют поверхностной и кулоновской энергии. Подстановка этого выражения в (10.1) дает
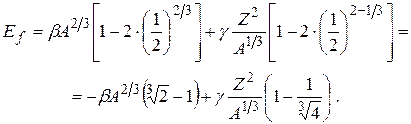
Отсюда следует, что деление энергетически выгодно (Ef > 0), когда
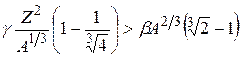 ,
,
или, после преобразований и подстановки коэффициентов β и γ,
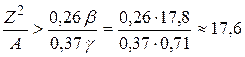 . (10.3)
. (10.3)
Величину Z 2/A называют параметром деления. Для циркония ( 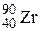 ) Z 2/A = 17,8. Таким образом, спонтанное деление энергетически выгодно для ядер всех элементов, начиная с циркония.
) Z 2/A = 17,8. Таким образом, спонтанное деление энергетически выгодно для ядер всех элементов, начиная с циркония.
10.2. Механизм деления.Почему же большинство ядер, представляющих вторую половину периодической системы элементов, устойчиво по отношению к спонтанному делению? Ответ на этот вопрос можно получить, рассматривая механизм деления. Простейшая теория деления была создана в 1939 г. Н. Бором и Д. Уилером, а также Я. Френкелем. В основу этой теории была положена капельная модель. В процессе деления жидкая капля-ядро последовательно проходит через следующие стадии (рис. 1): сфера (а), эллипсоид (б), гантель (в), два грушевидных осколка (г), два сферических осколка (д).
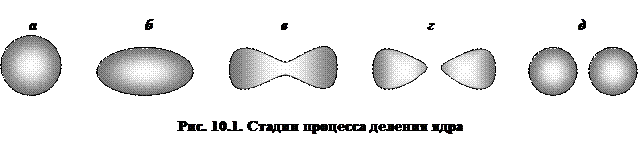
Как меняется энергия ядра на различных стадиях деления? Выше уже было показано, что такое изменение определяется изменением суммы поверхностной и кулоновской энергий материнского ядра. При деформации ядра энергия поверхностного натяжения капли увеличивается (именно поэтому в отсутствие внешних сил капля принимает шарообразную форму), а энергия кулоновского отталкивания протонов уменьшается (так как увеличивается среднее расстояние между ними). Таким образом, поверхностное натяжение стремится вернуть деформированное ядро в исходное состояние, а кулоновское отталкивание, напротив, способствует его делению. Отношение кулоновской энергии к поверхностной пропорционально параметру деления Z 2/A, который и определяет устойчивость ядра к деформации.
Чтобы приближенно оценить устойчивость произвольного ядра к малым деформациям и найти критическое значение параметра деления, будем считать, что исходное сферическое ядро принимает форму вытянутого эллипсоида вращения с малой и большой полуосями
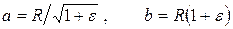 ,
,
где R – радиус материнского ядра, ε – малый параметр, который называется параметром деформации. Такой выбор полуосей продиктован условием, согласно которому объем ядра V при делении не меняется (ядерная материя практически несжимаема):
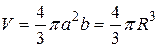 .
.
Вычисление поверхностной энергии сводится к геометрической задаче о площади поверхности эллипсоида вращения, а вычисление кулоновской энергии – к задаче о поле заряженного эллипсоида, если предположить, что заряд ядра равномерно распределен по объему. Для малых деформаций эллипсоида его поверхностная (WS) и кулоновская (WC) энергии могут быть записаны в виде ряда Тейлора по степеням ε. Вычисление при этом дает
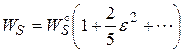 ,
,
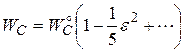 ,
,
где верхним индексом «о» обозначены величины соответствующих энергий недеформированного (сферического) ядра. Отсюда следует, что изменение полной энергии при переходе от сферы к эллипсоиду равно
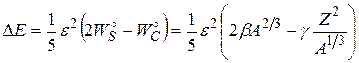 . (10.4)
. (10.4)
Критическое значение параметра деления определится из требования ΔЕ = 0, что эквивалентно требованию
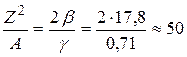 . (10.5)
. (10.5)
При значениях параметра деления > 50 ядро становится абсолютно неустойчивым к делению. Однако формулой (10.5) еще не определяются в отдельности критические значения Z и A, так как в общем случае между ними нет однозначной связи. Такая связь (формула (2.25) имеет место только в случае β-стабильных ядер. Подставляя (2.25) в (10.5) получаем иррациональное уравнение для А, решая которое, найдем критическое значение массового числа А ≈ 395 и критическое значение атомного номера Z ≈ 140. Таким образом, спонтанное деление ограничивает область существования устойчивых или долгоживущих ядер со стороны больших значений Z и A. Конечно, на полученные критические значения нужно смотреть как на сугубо ориентировочные, поскольку все они получены на основании капельной модели. Введение оболочечных поправок к энергии, даваемой капельной теорией, дает несколько иные результаты, однако качественно ничего не меняет. Проверка правильности теории возможна лишь путем синтеза элементов с атомными номерами, близкими к ожидаемой границе Z.
Вернемся к виду зависимости энергии ядра от параметра деформации. На рис. 10.2. показано изменение поверхностной и кулоновской энергии в процессе деления. Сложение этих двух кривых в общем случае может дать три различных варианта (рис. 10.3). На рисунке верхняя кривая относится к ядрам, в которых вклад поверхностной энергии при деформации превалирует над
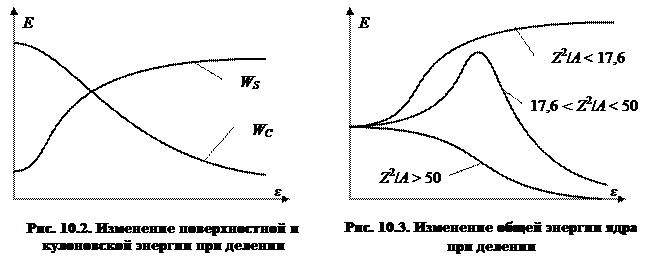
кулоновским вкладом (Z2/A < 17,6): в этом случае деление энергетически невыгодно. Нижняя кривая соответствует обратному случаю (Z2/А > 50): для таких ядер деление должно происходить мгновенно. Наконец, промежуточный случай реализуется при 17,6 < Z2/A < 50. На кривой зависимости энергии от параметра деформации появляется максимум – потенциальный барьер, который должен быть преодолен. В этом случае спонтанное деление происходит путем туннельного эффекта. Вероятность этого эффекта для осколков деления из-за их большой массы крайне мала. Так, в 1 г урана за 1 ч делится в среднем всего около 25 ядер. Отсюда можно рассчитать, что период полураспада урана по отношению к спонтанному делению составляет около 1016 лет, что в миллионы раз больше, чем период полураспада по отношению к испусканию α-частиц.
У трансурановых элементов[91] наблюдается конкуренция между α-распадом и спонтанным делением. Чем выше атомный номер элемента, тем больше его изотопов проявляют неустойчивость по отношению к делению, причем для некоторых последнее является единственным зарегистрированным видом распада.
10.3. Спонтанно делящиеся изомеры.Для ряда изотопов трансурановых элементов обнаружены возбуждённые состояния с очень малым периодом полураспада по отношению к спонтанному делению. Вероятность их спонтанного деления в среднем в 1026 раз превосходит вероятность деления соответствующих ядер в основном состоянии. Кроме того, для них свойственна очень сильная заторможенность изомерных переходов (при данной степени запрета по спину и четности). Например, 242mAm, открытый первым из ядер данного класса, ведет себя как смесь двух спонтанно делящихся радионуклидов с периодами полураспада 140 лет и 14 мс, причем во втором случае спонтанное деление является практически единственным каналом распада.
Объяснение природы этого явления было предложено Г.Н. Флеровым и В.М. Струтинским. Расчеты потенциального барьера деления для разных ядер, выполненные в рамках капельной модели с введением в нее оболочечных
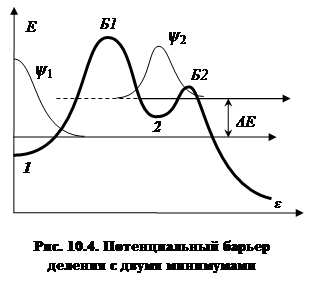 поправок, привели к любопытным результатам. Оказалось, что барьер деления в общем случае имеет форму не одного, а двух горбов, в результате чего при большой деформации ядра появляется второй минимум потенциальной энергии (рис. 10.4, ср. тж. рис. 10.3). Он соответствует возбужденному и достаточно долгоживущему, т.е. изомерному, состоянию ядра. Однако природа этой изомерии отличается от обычной, описанной в п. 9.3. В данном случае малая вероятность испускания γ-кванта объясняется не большой разностью спинов материнского и дочернего ядра, а большим барьером, разделяющим две потенциальные ямы. Дело в том, что волна, соответствующая состоянию ядра в области минимума 2, очень слабо проникает в область минимума 1 вследствие большой ширины и высоты внутреннего потенциального барьера Б1. Иными словами, перекрывание волновых функций ψ1 и ψ2 ничтожно мало. Но именно это перекрывание, помимо прочих факторов, и определяет вероятность изомерного перехода.[92] И, наоборот, большая вероятность спонтанного деления возбужденного состояния – следствие малой ширины и высоты внешнего барьера Б2. Что касается вероятности спонтанного деления из основного состояния, то оно определяется параметрами обоих барьеров.
поправок, привели к любопытным результатам. Оказалось, что барьер деления в общем случае имеет форму не одного, а двух горбов, в результате чего при большой деформации ядра появляется второй минимум потенциальной энергии (рис. 10.4, ср. тж. рис. 10.3). Он соответствует возбужденному и достаточно долгоживущему, т.е. изомерному, состоянию ядра. Однако природа этой изомерии отличается от обычной, описанной в п. 9.3. В данном случае малая вероятность испускания γ-кванта объясняется не большой разностью спинов материнского и дочернего ядра, а большим барьером, разделяющим две потенциальные ямы. Дело в том, что волна, соответствующая состоянию ядра в области минимума 2, очень слабо проникает в область минимума 1 вследствие большой ширины и высоты внутреннего потенциального барьера Б1. Иными словами, перекрывание волновых функций ψ1 и ψ2 ничтожно мало. Но именно это перекрывание, помимо прочих факторов, и определяет вероятность изомерного перехода.[92] И, наоборот, большая вероятность спонтанного деления возбужденного состояния – следствие малой ширины и высоты внешнего барьера Б2. Что касается вероятности спонтанного деления из основного состояния, то оно определяется параметрами обоих барьеров.
Одним из подтверждений модели ядра с двумя потенциальными барьерами является обнаружение у 240mPu конверсионных электронов, испускание которых опережает его спонтанное деление. По энергиям конверсионных электронов удалось восстановить спектр возбужденных состояний изомера, который был интерпретирован как вращательный (п. 4.5), соответствующий вытянутому эллипсоиду вращения с отношением полуосей b/a ≈ 2, что намного больше этого же отношения для 240Pu в основном состоянии.
Таким образом, спонтанно делящиеся изомеры, характеризующиеся высокой степенью деформации, следует классифицировать как изомеры формы. Изомеры формы известны у ~ 40 радионуклидов актиноидов, и лишь у двух из них (236mU и 238mU) наблюдается изомерный переход с испусканием γ-кванта. Энергия возбуждения изомеров формы ΔE (рис. 10.4) составляет от 2 до 4 МэВ, а периоды полураспада варьируются от наносекунд до миллисекунд. Наибольший период полураспада (14 мс) наблюдается у 242mAm.
10.4. Свойства осколков деления. Осколки – не единственный продукт деления. Отношение числа нейтронов к числу протонов в самых тяжелых ядрах (например, урана) ≈ 1,6, тогда как в ядрах с А = 120 – примерно 1,35. Следовательно, осколки в момент образования перегружены нейтронами и находятся в состояниях с большой энергией возбуждения. Очевидно, что они неустойчивы к β−-распаду, восстанавливающему протонно-нейтронный баланс. Часто осколки деления испытывают целую серию β−-распадов, в результате чего заряд первичного осколка увеличивается на 4-6 единиц.
Снятие начального возбуждения осколков происходит также путем вылета мгновенных нейтронов деления в момент разрыва гантелеобразного ядра, за время меньшее, чем 10−13 с. В среднем в каждом акте деления испускается 2-3 мгновенных нейтрона. Энергетический спектр таких мгновенных нейтронов непрерывный, с максимумом около 1 МэВ (средняя энергия – около 2 МэВ). Небольшая доля нейтронов (≈ 1%) испускается осколками после β−-распада из состояний с энергией возбуждения, превышающей энергию отделения нейтрона. Это происходит с некоторым запаздыванием (до 1 мин) относительно момента деления (запаздывающие нейтроны).
Часть энергии деления уносят γ-кванты, испускаемые возбужденными осколками сразу после вылета мгновенных нейтронов (т.н. мгновенное γ-излучение), а также γ-кванты, выделяющиеся в ходе сложного β−-распада.
Характерной особенностью деления является то, что осколки, как правило, существенно различаются по массам, т.е. преобладает асимметричное деление. Наиболее вероятно деление на осколки, один из которых примерно в 1,5 раза тяжелее другого. Вероятность симметричного деления примерно на три порядка меньше, чем деления в отношении 3:2. Хотя капельная модель не исключает самой возможности асимметричного деления, однако не объясняет происхождения асимметрии. Асимметрию деления объясняют влиянием оболочечной структуры: ядро стремится разделиться таким образом, чтобы основная часть нейтронов и в легком, и в тяжелом осколке образовала устойчивый магический остов (N = 50 и N = 82). С другой стороны, как показывают расчеты, учет оболочечных эффектов снижает высоту второго барьера деления при октупольной деформации (п. 4.5). В таком случае асимметричному делению способствует облегченный туннельный переход через второй потенциальный барьер при несимметричной (грушевидной) деформации.
10.5. Атомно-молекулярные последствия радиоактивного распада.Любой процесс радиоактивного распада, за исключением изомерного перехода, приводит к изменению заряда ядра. При этом, на первый взгляд, выброс ядром α- или β-частицы не затрагивает электронных оболочек атома: двигаясь со скоростью ~ 107-108 м/с, частицы покидают атом настолько быстро, что взаимодействием между ними и атомными электронами можно пренебречь. В связи с этим можно предположить, что после β+- или α-распада дочерний атом будет представлять собой отрицательный, а после β–-распада – положительный ион, так как в первом случае на атомных оболочках остаются «лишние» электроны (один или два), а во втором, напротив, имеет место нехватка одного электрона. Из тех же соображений можно ожидать, что после электронного захвата дочерний атом будет электрически нейтральным.
В действительности образования отрицательных ионов после радиоактивного распада не наблюдается вообще. Так, например, после β+-распада 79Kr дочерний 79Br имеет положительный заряд: от +1 до +13. В то же время 85Rb после β–-распада 85Kr также образуется в состоянии многократно заряженного положительного иона: до +10. Наконец, при электронном захвате 37Ar дочерний 37Cl с наибольшей (около 40%) вероятностью оказывается в состоянии Cl3+.[93]
Причина образования после распада положительных ионов заключается в том, что «мгновенное» изменение заряда ядра возмущает атомные электронные уровни (эффект встряски). Если рассматривать этот процесс с точки зрения квантовой механики, уровни дочернего атома (иона) после распада уже не будут являться стационарными. В частности, увеличение Z должно приводить к более сильному связыванию внутренних электронов с ядром, а уменьшение – наоборот, к более слабому. Тем не менее, конечное состояние системы должно быть одним из стационарных состояний дочернего атома (иона). Возмущение, вносимое в систему изменением заряда ядра, может приводить к возбуждению и даже к ионизации дочернего атома. Необходимая для этого энергия – это некоторая (небольшая) доля энергии испускаемой ядром частицы. Вероятность ионизации обратно пропорциональна квадрату эффективного атомного номера материнского ядра Z*, значение которого меньше действительного Z вследствие экранирования ядра внутренними электронами.[94]
При электронном захвате (как и при внутренней конверсии γ-квантов) эффект встряски играет второстепенную роль. Ионизация дочернего атома здесь вызвана, главным образом, испусканием им самим электронов Оже.
Распад радиоактивных ядер в составе молекул приводит к образованию положительных молекулярных ионов, при этом последние могут диссоциировать. Так, при распаде радиоуглерода в 14CO2 образуются (NO2)+, (NO2)2+, (NO)+, (NO)2+, O+, O2+, N+, N2+ и даже O2+. Диссоциация дочерних молекул объясняется, с одной стороны, возможностью электронов образовать молекулярные орбитали, не соответствующие связанным состояниям, с другой – кинетической энергией ядер отдачи, часть которой может пойти на разрыв химических связей.
