Дифракция в параллельных лучах

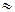Дифракциясвета – это огибание световыми волнами препятствий. Препятствиями служат узкие щели, малые отверстия, непрозрачные экраны. При этом размер препятствия d сравним с λ длиной волны.d λ. Дифракция света объясняется на основе принципа Гюйгенса-Френеля: Любая точка пространства, до которой дошло колебание, становится источником вторичных когерентных волн.

Интерференция этих волн определяет освещенность в данной точке экрана (пространства). Дифракционная картина – чередование светлых и темных полос.

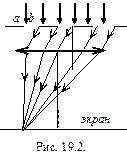Дифракция в параллельных лучах наблюдается на щели и на дифракционной решетке. Пусть ширина щели b, на щель падает плоская волна. Согласно принципу Гюйгенса, каждая точка щели порождает вторичную сферическую волну. За щелью помещают собирающую линзу, а в фокальной плоскости этой линзы – экран (рис.19.1). Тогда волны одного направления собираются в определенной точке экрана. Эти волны когерентны и при наложении интерферируют. Результат их интерференции и определяет распределение интенсивности на экране. Дифракционная картина от щели представляет собой чередование светлых и темных полос (максимума и минимума освещенности). Условие минимума при дифракции от щели:

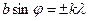(19.1)

Условие максимума при дифракции от щели:

(19.2)

Система узких параллельных щелей, разделенных непрозрачными промежутками, называется дифракционной решеткой. Обычно решетки изготовляются с помощью специальной делительной машинки, наносящей на стеклянной пластине параллельные штрихи. Число штрихов доходит до нескольких тысяч на 1 мм. Бывают также отражательные решетки. Они представляют собой чередующиеся участки, отражающие свет и рассеивающие его. Рассеивающие свет штрихи наносятся резцом на отшлифованной металлической пластине. Если ширина прозрачных щелей (или отражающих полос) b, а ширина непрозрачных промежутков а, то величина называется периодом (или постоянной) решетки (рис.19.2). Каждая точка каждой щели дифракционной решетки посылает вторичные сферические волны. Когерентные лучи одного направления фокусируются с помощью линзы в определенной точке экрана. Распределение интенсивности на экране определяется двумя явлениями: 1) дифракцией на каждой щели и 2) наложением когерентных пучков от всех щелей (многолучевая интерференция). Картина представляет собой систему узких и ярких полос, называемых главными максимумами, на темном фоне. Вторичные максимумы слабы по сравнению с главными и практически не видны. Положение главных максимумов определяется условием: 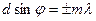(20.3)

где m = 0,1,2,3 - порядок главных максимумов

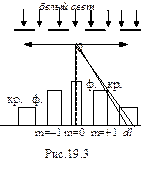Из соотношения (20.3) видно, что угол дифракции зависит от длины волны: 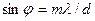(20.4)

Так как 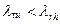, то 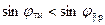при . Из этого следует, что при освещении решетки белым светом, все максимумы, кроме максимума нулевого порядка, представляют собой спектры, фиолетовым концом обращенные к максимуму нулевого порядка (рис.20.3). Следовательно, решетка разлагает сложный свет по длинам волн. Поэтому дифракционную решетку используют как спектральный прибор и для точного измерения длин волн.

Поляризация света.

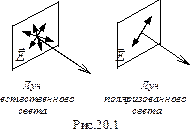
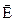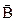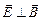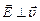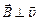Свет, как электромагнитная волна, характеризуется колебаниями вектора (вектор напряженности переменного электрического поля) и вектора , (вектора индукции переменного магнитного поля). При этом и , , где 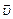– вектор скорости распространения волны. Следовательно, свет – это поперечная электромагнитная волна.

Световая волна, в которой колебания вектора 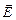в плоскости, перпендикулярной направлению распространения, непрерывно изменяется, называется естественной. Волна, в которой колебания вектора 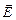в указанной плоскости фиксировано, называется поляризованной (рис. 20.1).

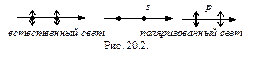Так как любое линейное колебание вектора 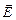можно разложить на два взаимно перпендикулярных, то условные обозначения естественного и поляризованного света (рис.20.2).

Устройства, превращающее естественный свет в поляризованный, называется поляризатором, а устройство, с помощью которого определяют каким является свет, называются анализатором (рис.20.3).

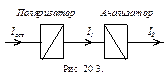Плоскость, в которой колеблется 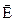после прохождения поляризатора, анализатора, называется главной плоскостью поляризатора (анализатора). При прохождении света через систему поляризатор-анализатор интенсивность света меняется по закону Малюса 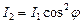, , 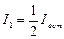где 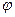– угол между главными плоскостями поляризатора и анализатора.

Поляризованный свет можно получить при отражении от диэлектрика, при преломлении, с помощью различных кристаллов. При падении света на поверхность диэлектрика происходит частичное отражение и преломление (рис.20.4). Если на поверхность диэлектрика падает свет под углом Брюстера i_Б, удовлетворяющего условию: 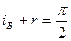или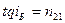, отраженный свет будет полностью поляризованным. Закон 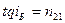носит название закона Брюстера

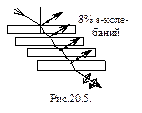
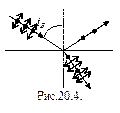Если взять стопу стеклянных пластин, сложенных вместе, на которые падает свет под углом i_Б, тогда 8% падающего света отражается, причем отраженный свет содержит только s-колебания. В падающем свете 50% составляет s -колебания, а 50% – p-колебания. На поверхности каждой пластины отражается 8% s-колебаний, поэтому прошедший через стопу свет содержит преимущественно p -колебания. Такое устройство, позволяющее получить поляризованный свет, называется стопой Столетова.

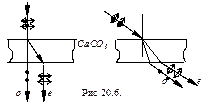При прохождении света через кристалл (кроме кристаллов кубической симметрии) луч света раздваивается. Для одного луча выполняется закон преломления. Такой луч – обыкновенный “о”: 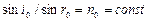. Для необыкновенного луча “е”: 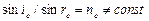.Необыкновенный луч не лежит в одной плоскости с падающим лучом и перпендикулярен к границе раздела. В кристаллах имеется направление, вдоль которого не происходит двойного лучепреломления. Оно называется оптической осью кристалла. Плоскость, проходящая через оптическую ось и падающий луч, называется главным сечением кристалла. Оба луча, обыкновенный и необыкновенный, являются поляризованными, причем плоскости их поляризации взаимно перпендикулярны. Считается, что для обыкновенного луча вектор 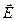колеблется перпендикулярно плоскости главного сечения, а для необыкновенного луча – колебания вектора 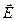параллельны плоскости главного сечения (рис. 20.6).

Поляризация при двойном лучепреломлении объясняется анизотропией кристаллов (т.е. неодинаковостью их свойств по разным направлениям). По электромагнитной теории: 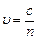; 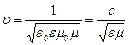. Для диэлектриков (какими являются кристаллы) 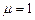,а значит 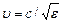. Отсюда получим 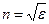. При падении на кристалл естественного света колебаниям вектора 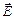, перпендикулярным плоскости главного сечения, соответствует одно значение диэлектрической проницаемости - 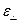, а для колебаний вектора 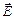параллельных плоскости главного сечения, - другое значение - . Поэтому различным направлениям колебания вектора 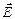соответствуют различные значения 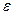и показателя преломленияn: 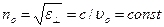; ; 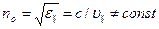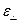¹; 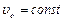; ; .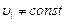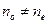