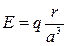Поле бесконечной однородно заряженной плоскости

Поверхностная плотность заряда на произвольной плоскости площадью S определяется по формуле:

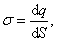
где dq – заряд, сосредоточенный на площади dS; dS – физически бесконечно малый участок поверхности.

Пусть σ во всех точках плоскости S одинакова. Заряд q – положительный. Напряженность 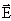во всех точках будет иметь направление, перпендикулярное плоскости S (рис. 2.11).

Очевидно, что в симметричных, относительно плоскости точках, напряженность 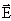будетодинакова по величине и противоположна по направлению.

Представим себе цилиндр с образующими, перпендикулярными плоскости, и основаниями ΔS, расположенными симметрично относительно плоскости (рис. 2.12).

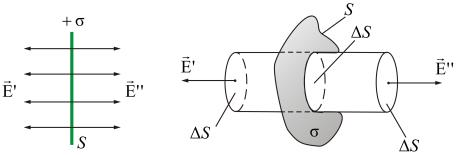	Рис. 2.11	Рис. 2.12

Тогда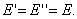

Применим теорему Остроградского-Гаусса. Поток Ф_Е через боковую часть поверхности цилиндра равен нулю, т.к. 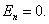Дляоснования цилиндра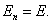

Суммарный поток через замкнутую поверхность (цилиндр) будет равен:

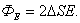
Внутри поверхности заключен заряд 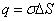. Следовательно, из теоремы Остроградского–Гаусса получим:

;

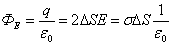откуда видно, что напряженность поля плоскости S равна:

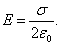(2.5.1)

Полученный результат не зависит от длины цилиндра. Это значит, что на любом расстоянии от плоскости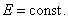

с обзорки

Рассмотрим бесконечную заряженную поверхность с поверхностной плотностью зарядов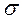

Используем терему Гаусса в интегральной форме

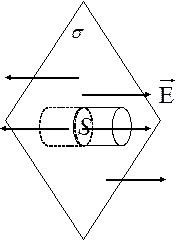
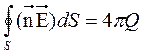
Поток вектора через поверхность цилиндра равен сумме потоков через основание и боковую поверхность цилиндра.

Вектор напряженности электрического поля E направлен перпендикулярно к заряженной поверхности поэтому поток через боковую поверхность цилиндра равен нулю.

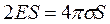
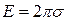
Напряженность поля бесконечно заряженной плоскости не зависит

от расстояния, а зависит только от .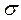

Найдем напряженность поля создаваемую заряженным диэлектрическим шаром.

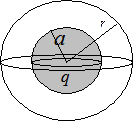1) Сначала рассмотрим случай когда .

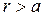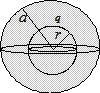
Вокруг заряженного шара построим

воображаемую сферу, через которую

найдем поток напряженности

электрического поля. Используя теорему Гаусса в

дифференциальной форме получим

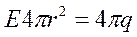
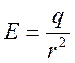, т.е напряженность поля заряженного шара выражается такой же формулой как и для точечного заряда.

2) Если 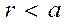то, используя теорему

Гаусса получим

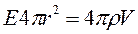, где V- это обьем

воображаемой сферы

Отсюда получим, что напряженность поля внутри заряженного шара равна