Описание лабораторных макетов

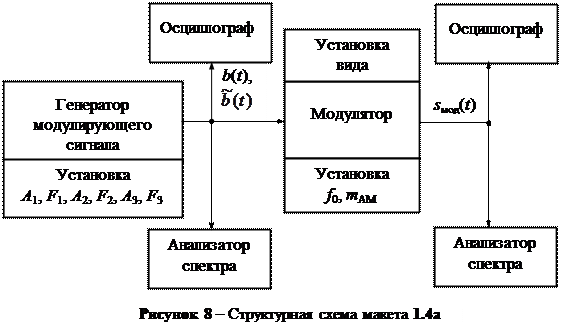
Лабораторная работа по исследованию сигналов АМ, БМ и ОМ выполняется на компьютере с использованием виртуального макета 1.4а, структурная схема которого приведена на рис. 8.

В состав макета входят генератор модулирующего непрерывного сигнала b(t) = A₁sin(2pf₁t) + A₂sin(2pf₂t) + A₃sin(2pf₃t) и модулятор (генератор несущего колебания входит в состав модулятора). Значения частот и амплитуд гармонических колебаний A₁, f₁, A₂, f₂, A₃, f₃, частоту переносчика f₀, коэффициент m_АМ можно изменять.

Схема макета дает возможность устанавливать вид модуляции: АМ, БМ, ОМ с ВБП и ОМ с НБП. Временные и спектральные диаграммы сигналов можно наблюдать в двух точках схемы макета: на входе и на выходе модулятора. В случае ОМ осциллографом на входе модулятора кроме модулирующего сигнала b(t) отображается сигнал 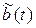. Вместе с осциллограммой модулированного сигнала пунктирной линией выводится график огибающей сигнала.

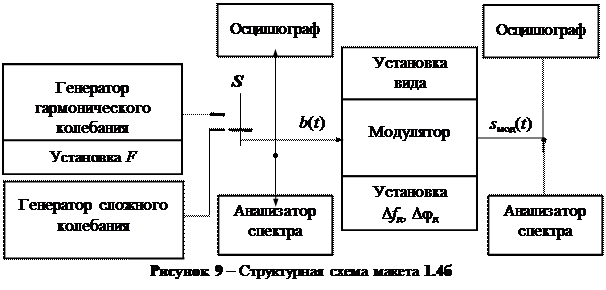
Лабораторная работа по исследованию сигналов ЧМ и ФМ выполняется на компьютере с использованием виртуального макета 1.4б, структурная схема которого приведена на рис. 9.

В состав макета входят модулятор и генераторы модулирующих сигналов. Частота переносчика f₀ = 2500 Гц. Переключатель S дает возможность выбирать один из генераторов модулирующих сигналов: генератор гармонического колебания b(t) = sin 2pft, частоту которого f можно регулировать, и генератор сложного колебания b(t) = 0,5 sin 2p70t + 0,5 sin 2p200t.

Схема макета дает возможность устанавливать вид модуляции: ЧМ или ФМ, девиацию частоты Df_д в случае ЧМ и девиацию фазы Dj_д в случае ФМ. Временные и спектральные диаграммы сигналов можно наблюдать в двух точках схемы макета: на входе и на выходе модулятора.

Требования к отчету

7.1 Название лабораторной работы.

7.2 Цель работы.

7.3 Результаты выполнения домашнего задания.

7.4 Структурные схемы для выполнения каждого пункта лабораторного заданияи результаты выполнения пп. 5.2...5.4, 5.6…5.9 лабораторного задания (осциллограммы и спектрограммы, каждая из которых должна иметь подпись).

7.5 Выводы из результатов выполнения пп. 5.2...5.4, 5.6…5.9 лабораторного задания (совпадение теоретических и экспериментальных данных, совпадение результатов выполнения домашнего задания и экспериментальных данных, проявление свойств сигналов и т.п.).

7.6 Дата, подпись студента, виза преподавателя с оценкой в 100-балльной шкале.

ЛР 1.5 Исследование сигналов цифровой модуляции

Цель работы

1.1 Изучение методов передачи цифровых сигналов модулированными сигналами АМ-М, ФМ-М и ЧМ-2.

1.2 Исследование временных и спектральных характеристик сигналов АМ-М и ФМ-М для М = 2 и 4 и ЧМ-2.

Ключевые положения

2.1 Первичный цифровой сигнал b(t) – это последовательность двоичных символов (бит) 1 и 0, следующих через интервал Т_б. В цифровых устройствах прямоугольный импульс высокого уровня соответствует символу 1, а импульс низкого уровня – символу 0. Основной параметр первичного цифрового сигнала – его скорость R (бит/с).

2.2 Сигнал цифровой модуляции s(t) – это последовательность радиоимпульсов, которые отображают первичный сигнал и следуют через тактовый интервал Т:

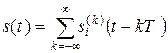, (1)

где s_i(t), i = 0, …, М – 1 – канальные символы (радиоимпульсы);

М – число канальных символов (уровней модулированного сигнала);

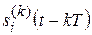– i-й канальный символ, передаваемый на k-м тактовом интервале.

Радиоимпульсы могут отличаться амплитудами, фазами или частотами. Существуют разные виды цифровой модуляции: АМ-М, ФМ-М, АФМ-М, КАМ‑М, ЧМ-М.

Если М = 2, то имеет место двоичный сигнал s(t), когда символ s₀(t) используется для передачи 0, а символ s₁(t) – для передачи 1. Если М > 2, то имеет место многопозиционный (многоуровневый) сигнал s(t). Как правило, М = 4, 8, …, 2ⁿ, n – целое число. Здесь каждый символ s_i(t) используется для передачи n = log₂M бит первичного сигнала b(t). Какую именно последовательность бит переносит каждый символ, устанавливает модуляционный код. Если в случае двоичных сигналов Т = Т_б, то в случае многопозиционных сигналов длительность тактового интервала увеличивается: Т = Т_бlog₂M.

2.3 Для сигналов АМ-М и ФМ-2 канальные символа записываются:

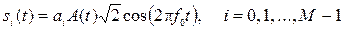, (2)

где a_i – число, отображающее n бит, которые передаются символом s_i(t);

A(t) – функция, определяющая форму радиоимпульсов;

f₀ – частота несущего колебания.

Из выражения (2) вытекает, что канальные символы являются сигналами аналоговой БМ и, поэтому спектр радиоимпульса s_i(t) состоит из двух боковых полос, сосредоточенных возле частоты несущей f₀. Спектральные свойства радиоимпульса s_i(t) целиком определяются функцией A(t).

Если функция A(t) – прямоугольный импульс длительности Т, то спектр радиоимпульса будет широким, а для передачи цифровых сигналов важно сформировать компактный спектр. Для того чтобы спектр радиоимпульса s_i(t) был компактным, и отсутствовала межсимвольная интерференция, функция A(t) должна быть импульсом Найквиста. Тогда боковые полосы частот будут копиями спектра Найквиста (рис. 1), а ширина спектра сигналов АМ-М и ФМ-2:

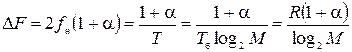, (3)

где f_н = 0,5/Т – частота Найквиста;

a – коэффициент ската спектра (0 £ a £ 1).

Из выражения (3) вытекает важный вывод – увеличение числа позиций сигнала позволяет уменьшить ширину спектра канальных символов (2).

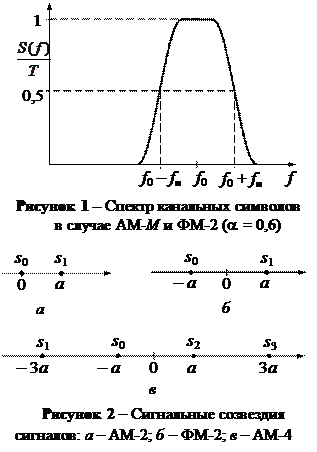2.4 Канальные символы принято условно изображать в виде сигнальных точекв некотором пространстве. Сигнальные точки сигналов АМ-М и ФМ‑2 располагаются на числовой оси и потому эти сигналы называют одномерными (рис. 2). Диаграммы, на которых канальные символы изображены в виде сигнальных точек, называются сигнальными созвездиями.

Модуляционный код сигнала
АМ-2: передаче 0 соответствует a₀ = 0, а передаче 1 соответствует a₁ = а.

Модуляционный код сигнала
ФМ-2:0 ® a₀ = – а; 1 ® a₁ = а.

Модуляционный код сигнала
АМ-4:00 ® a₀ = – а; 01 ® a₁ = – 3а; 10 ® a₂ = а; 11 ® a₃ = 3а. Число а определяет энергии канальных символов.

2.5 Канальные символы s_i(t) в случае ФМ-М (М ³ 4) и АФМ-М в общем виде описываются с помощью синфазной и квадратурной составляющих:

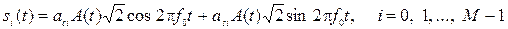, (4)

где a_ci, a_si – коэффициенты, отображающие последовательность из n бит, которая передается канальным символом s_i(t).

Сигналы, описываемые выражением (4), являются суммой двух БМ сигналов с одинаковыми амплитудными спектрами, которые определяются спектром сигнала A(t). В случае, если A(t) – импульс Найквиста, амплитудный спектр каждой из составляющих, а также их суммы, имеет вид, показанный на рис. 1. Поэтому ширина спектра канальных символов в случае ФМ-М и АФМ-М описывается выражением (3).

2.6 Сигналы АФМ-М и ФМ-М (М ³ 4) являются двумерными, поскольку функци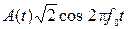и и 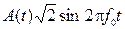, присутствующие в выражении (4), ортогональные и образуют двумерное пространство. Сигнальные созвездия двумерных сигналов изображаются на плоскости (рис. 3). Здесь х символизирует колебание 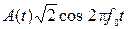, а y – .

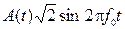Для сигналов ФМ-М выражение (4) можно переписать:

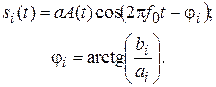(5)

Модуляционный код сигнала ФМ-4:

00 ® j₀ = 135° (a_с0 = – а и a_s0 = а);

01 ® j₁ = 45° (a_c1 = а и a_s1 = а);

10 ® j₂ = 225° (a_c2 = – а и a_s2 = – а);

11 ® j₀ = 315° (a_c3 = а и a_s3 = – а).

2.7 Процесс формирования одномерных и двумерных сигналов на основе выражений (2) и (4) такой: кодер модуляционного кода ставит в соответствие n = log₂M входным битам два П-импульса с амплитудами a_сi и а_si (в случае одномерных сигналов один импульс с амплитудой a_сi, а а_si = 0); П-импульсы фильтруются формирующими ФНЧ так, чтобы получить импульсы Найквиста; импульсы a_сiА(t) и а_siА(t) поступают на входы балансных модуляторов; полученные модулированные сигналы суммируются.

2.8 Сигнал ЧМ-2 строится на основе радиоимпульсов, которые отличаются частотами:

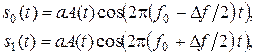
(6)

где Df – разнос частот;

а – коэффициент, определяющий энергию канальных символов.

Пусть функция A(t) – П-импульс длительности Т с амплитудой 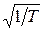, а j₀ = j₁ = 0. Легко убедиться, что в этом случае скалярное произведение сигналов s₀(t) и s₁(t):

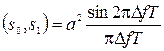. (7)

Итак, канальные символы (6) ортогональные, когда разнос частот

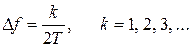(8)

Рассмотрим случай, k = 1, т.е. Df = 0,5/T. Сигнал ЧМ-2 на одном тактовом интервале записывается

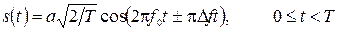, (9)

где знак «+» соответствует s₁(t), а знак «–» соответствует s₀(t).

Из (9) видно, что на тактовом интервале имеет место линейное изменение фазы несущего колебания cos2pf₀t, а в момент Т набег фазы составляет p/2.

Модуляция ЧМ-2 называется модуляцией минимального сдвига (ММС) в случае выполнения следующих условий:

1. У канальных символов (6) функция A(t) – П-импульс длительности Т.

2. Разнос частот Df = 0,5/T.

3. Модулированный сигнал формируется без “разрыва” фазы.

Последнее условие реализуется следующим образом: фаза несущего колебания cos2pf₀t в начале следующего тактового интервала совпадает с фазой в конце предыдущего тактового интервала, должно быть накопления фазы без “разрыва”. Для этого символы цифрового сигнала отображаются в П-импульсы длительности Т и амплитуды d_k (k – номер тактового интервала): 1 ® d_k = 1, 0 ® d_k = –1. Тогда изменение фазы Dj(t) без “разрыва” для любого момента времени t = nТ + Dt можно записать

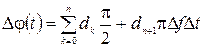. (10)

Здесь П-импульсы амплитуды d_k выступают в роли множителей к функции pDfDt. Для первичного цифрового сигнала b(t) = {1, 0, 0, 1} на рис. 4 приведено изменение фазы Dj(t) без “разрыва”.

Сигнал ММС на бесконечном интервале записывается

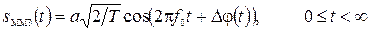, (11)

где Dj(t) – изменение фазы, определяемое выражением (10).

Представим сигнал s_ММС(t) через квадратурные составляющие:

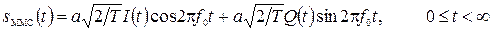, (12)

где I(t) = cosDj(t) – косинусная составляющая;

Q(t) = –sinDj(t) – синусная составляющая.

Для первичного цифрового сигнала b(t) = {1, 0, 0, 1} на рис. 4 показаны квадратурные составляющие. Представление сигнала s_ММС(t) через квадратурные составляющие лежит в основе построения схемы модулятора.

Нормированный спектр модулированного сигнала ММС описывается выражением

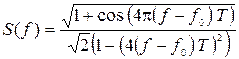. (13)

Зависимость (13) приведена на рис. 5. С увеличением ïf – f₀ï спектр убывает со скоростью 1/(f – f₀)². Если ширину спектра F_ммс определить по первым нулям зависимости (13), то

F_ммс = 1,5/Т. (14)

2.9 Для того, чтобы получить сигнал ЧМ-2 с узким спектром и не было межсимвольной интерференции, необходимо, чтобы функция A(t) была импульсом Найквиста. В таком случае можно считать, что спектр сигнала s_ЧМ-2(t) есть сумма спектров двух радиоимпульсов частот ¦₀ - D¦/2 и ¦₀ + D¦/2. На рис. 6 показан нормированный спектр сигнала ЧМ-2, из которого вытекает, что разнос частот будет минимальным, когда спектры радиоимпульсов примыкают друг к другу, и он равняется:

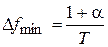. (15)

Тогда ширина спектра сигнала ЧМ-2:

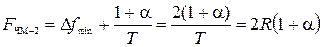, (16)

вдвое больше ширины спектра сигналов АМ-2 и ФМ-2.

Формирование сигналов ЧМ-2 отличается от формирования сигналов ФМ-М работой кодера модуляционного кода и тем, что частоты опорных колебаний генераторов в балансных модуляторах отличаются на величину D¦/2 от частоты несущего колебания.

Ключевые вопросы

3.1 С какой целью используется модуляция в системах электросвязи?

3.2 Дайте определение цифрового сигнала.

3.3 Сформулируйте принцип цифровой модуляции.

3.4 Дайте определение сигналов цифровых видов модуляции АМ-М, ФМ‑М и ЧМ-М.

3.5 Почему для передачи цифровых сигналов каналами связи не используются радиоимпульсы с П-образной огибающей? Какой должна быть огибающая импульса?

3.6 Как рассчитать ширину спектра сигналов АМ-М, ФМ-М и ЧМ-2?

3.7 Дайте определение сигналов модуляции минимального сдвига.

3.8 С какой целью для передачи цифровых сигналов каналами связи используются многопозиционные сигналы?

3.9 Какие сигналы цифровых видов модуляции являются одномерными, а какие – двумерными?

Домашнее задание

4.1 Изучить раздел "Цифровые виды модуляции" по конспекту лекций и литературе [1, с. 91...120; 3, с. 164...168, 180...185; 4, с. 103...112] и описание лабораторного макета в разд. 6.

4.2 Задана длительность тактового интервала Т = 50 мс. Необходимо построить временные диаграммы канальных символов s₁(t) с частотой ¦₀ = 40 Гц для двух случаев: с П-образной огибающей и огибающей в виде импульса Найквиста.

Примечание. Необходимо учитывать, что канальным символом является произведение П-импульса длительности Т или импульса Найквиста и гармонического колебания. В качестве импульса Найквиста можно взять функцию

,

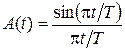а график канального символа построить на интервале (– 4Т, 4Т).

4.3 Подготовиться к беседе по ключевым вопросам.

Лабораторное задание

5.1 Ознакомиться с виртуальным макетом на рабочем месте. Для этого запустить программу 1.5 Исследование сигналов цифровой модуляции, используя иконку Лабораторные работы на рабочем столе, а затем папки ТЭС и Модуль 1. Изучить схему макета на дисплее компьютера, пользуясь разд. 6. Уточнить с преподавателем план выполнения лабораторного задания.

5.2 Подготовка макета. Необходимо установить цифровой сигнал, для чего представить десятичное число 128 + 10N (N – номер Вашей бригады) в двоичной системе исчисления. Коэффициент ската спектра рассчитывается по формуле: a = 1 ‑ 0,1N.

5.3 Исследование зависимости формы и спектра сигналов АМ-2 и АМ-4 от формы огибающей.Для этого необходимо установить: вид модуляции АМ-2; форму огибающей П-импульс. Зафиксировать в протоколе одну под другой временные диаграммы следующих сигналов: цифрового сигнала, сигналов на выходах кодера модуляционного кода, модулированного сигнала. Также зафиксировать спектральную диаграмму модулированного сигнала. После этого установить форму обводной импульс Найквиста. Зафиксировать в протоколе временную и спектральную диаграммы модулированного сигнала. Такие же исследования выполнить для сигнала АМ-4.

В выводах на основе сравнения спектральных диаграмм указать целесообразность использования радиоимпульсов с огибающей в форме импульса Найквиста и целесообразность использования многопозиционных сигналов для уменьшения занимаемой полосы частот.

5.4 Исследование зависимости формы и спектра сигналов ФМ-2 и ФМ-4 от формы огибающей. Повторить исследования, проведенные в п. 5.3, для сигналов ФМ-2 и ФМ-4. Сравнить спектры сигналов АМ-М и ФМ-М.

5.5 Исследование формы и спектра сигнала ЧМ-2 на основе импульсов Найквиста.Для этого необходимо установить: вид модуляции ЧМ‑2; форму огибающей – импульс Найквиста. Зафиксировать в протоколе одну под другой временные диаграммы следующих сигналов: цифрового сигнала, сигналов на выходах кодера модуляционного кода, модулированного сигнала. Также зафиксировать спектральную диаграмму модулированного сигнала.

5.6 Исследование формы и спектра сигнала ММС.Для этого необходимо установить: вид модуляции ЧМ-2; форму огибающей – П-импульс. Зафиксировать в протоколе одну под другой временные диаграммы следующих сигналов: цифрового сигнала, сигналов на выходах кодера модуляционного кода, модулированного сигнала. Также зафиксировать спектральную диаграмму модулированного сигнала. Объяснить форму квадратурных составляющих сигнала a_i(t) i b_i(t). Для этого необходимо начертить график изменение фазы Dj(t) по аналогии с рис. 4.

Сравнить спектры сигналов АМ-2, ММС и ЧМ-2 на основе импульсов Найквиста.