Концентрационная колориметрия
Нижегородская государственная сельскохозяйственная академия
НЕКОТОРЫЕ РАЗДЕЛЫ
ОПТИКИ
Нижний Новгород 2006г.
Нижегородская государственная сельскохозяйственная академия
НЕКОТОРЫЕ РАЗДЕЛЫ
ОПТИКИ
Методическое пособие по физическим разделу
Теоретических основ прогрессивных технологий (ТОПТ)
Для студентов экономического факультета
сельскохозяйственных ВУЗов
Нижний Новгород 2006 г.
Автор: А.А. Гаврилова
УДК 539.19+536
НЕКОТОРЫЕ РАЗДЕЛЫ ОПТИКИ:
методическое пособие по физическиму разделу Теоретических основ прогрессивных технологий (ТОПТ). Для студентов экономического факультета сельскохозяйственных ВУЗов/ Нижегородская гос. с.-х. академия. -Нижний Новгород, 2006г.
Учебное пособие составлено в соответствии с действующими программами по ТОПТ для студентов экономических специальностей сельскохозяйственных ВУЗов и включает в себя теорию по некоторым разделам «Оптики».
Печатается по решению редакционно-издательского совета Нижегородской государственной сельскохозяйственной академии
Под редакцией д.б.н. профессора А. В.Чурмасова
Рецензенты: кафедра физики НГСХА;
© Нижегородская государственная
сельскохозяйственная академия, 2006г.
ГЕОМЕТРИЧЕСКАЯ
ОПТИКА
И
ФОТОМЕТРИЯ
ЗАКОНЫ ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ СВЕТА
Раздел оптики, в котором законы распространения света рассматриваются на основе представления о световых лучах, называется геометрической оптикой. Под световыми лучами понимают нормальные к волновым поверхностям линии, вдоль которых распространяется поток световой энергии.
На границе раздела двух прозрачных однородных сред свет частично отражается, а частично проходит во вторую среду, изменяя при этом свое направление. Закон отражения: отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения; угол отражения α равен углу падения β:
α = β (1)
Направление распространения светового луча в этих средах определяется законом преломления Снеллиуса: преломленный луч лежит в той же плоскости, в которой находятся падающий луч и нормаль к разделу сред, восстановленная в точке падения; отношение синуса угла падения (α) и угла преломления (γ) есть величина постоянная для данной пары сред:
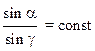 (2)
(2)
Значение постоянной величины (const) можно определить из волновой теории света (рис. 1). Пусть «ММ» - граница двух сред, в которых свет распространяется с разными скоростями v1 и v2 (причем v1 > v2). Под некоторым углом α на границу ММ падает параллельный пучок световых лучей. Выберем в этом потоке два луча SA и SB. AC – фронт падающих лучей. Согласно принципу Гюйгенса, каждую точку волнового фронта следует рассматри-
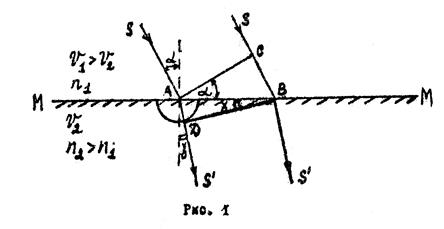 ватькак самостоятельный источник новых волн. Следовательно, но, пока второй луч SB дойдет до точки В, около точки А возникает полусферическая волна с радиусом AD, причем AD < CB, т. к. v2 < v1. Фронтом новой волны по принципу Гюйгенса будет ВD – касательная, проведенная из точки B к AS′ – направлению преломленного луча, поэтому BD ┴ ADS′. Угол между нормалью к границе ММ и преломленным лучем ADS′ – угол преломления γ. Из геометрических соображений (углы, образованные взаимноперпендикулярными сторонами) угол САВ равен углу α, угол ADB равен углу γ. Из прямоугольных треугольников АСВ и ADB можем написать: СВ = АВ·sin α ; AD = AB · sin α. Разделив эти уравнения, получим:
ватькак самостоятельный источник новых волн. Следовательно, но, пока второй луч SB дойдет до точки В, около точки А возникает полусферическая волна с радиусом AD, причем AD < CB, т. к. v2 < v1. Фронтом новой волны по принципу Гюйгенса будет ВD – касательная, проведенная из точки B к AS′ – направлению преломленного луча, поэтому BD ┴ ADS′. Угол между нормалью к границе ММ и преломленным лучем ADS′ – угол преломления γ. Из геометрических соображений (углы, образованные взаимноперпендикулярными сторонами) угол САВ равен углу α, угол ADB равен углу γ. Из прямоугольных треугольников АСВ и ADB можем написать: СВ = АВ·sin α ; AD = AB · sin α. Разделив эти уравнения, получим:
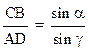 (3)
(3)
Теперь разделим числитель и знаменатель левого отношения равенства (3) на промежуток времени Δt, за который свет проходит путь СВ в первой среде и путь AD во второй среде:
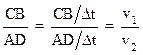 (4)
(4)
Объединив уравнения (3) и (4), получим:
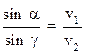 (5)
(5)
Так как абсолютный показатель преломления среды (n) равен отношению скорости света (с) в вакууме к скорости света (v) в данной среде, то можно записать:
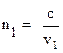 и
и 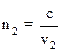 (6)
(6)
Равенство (4) с учетом формул (5) примет вид:
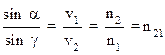 (7)
(7)
где n21 - относительный показатель преломления двух сред. Соотношение (7) – закон преломления света на границе двух сред.
Показатель преломления является важной индивидуальной физической характеристикой вещества. Он принадлежит к тем физическим величинам, которые можно измерить с высокой степенью точности и небольшой затратой времени, располагая малым количеством вещества.
Оптические методы исследования веществ, основанные на измерении их показателей преломления, составляют самостоятельный раздел прикладной оптики – рефрактометрию. Рефрактометрические данные можно использовать для определения чистоты вещества и концентрации вещества в растворе, для идентификации различных веществ и т. п.
При переходе света (рис. 2а) из среды с меньшим показателем преломления (оптически менее плотная) в среду с большим показателем преломления (оптически более плотная) угол падения больше угла преломления
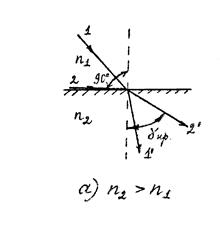 | 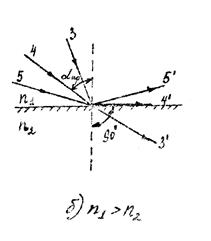 |
Рис 2
(лучи 1 и 1′). Если угол падения луча 2 близок к прямому (α = 90˚, луч ْ2 скользит вдоль границы раздела сред), то он будет преломляться под углом γпр (луч 2′). Этот угол является наибольшим углом преломления для данных сред и называется предельным углом преломления. Из закона преломления следует:
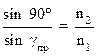 или
или 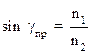 (8)
(8)
Если свет переходит из оптически более плотной среды в оптически менее плотную (рис. 2б), то угол преломления больше угла падения (лучи 3 и 3′). При некотором угле падения αпр (луч 4) угол преломления равен 90˚, т. е. преломленный луч 4′ скользит вдоль границы сред. При дальнейшем увеличении угла падения света луч 5 полностью отражается (луч 5′) от границы сред возникает явление полного внутреннего отражения. Из формулы (7):
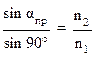 или
или 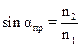 (9)
(9)
Угол αпр называется предельным углом полного отражения. Из формул (8) и (9) следует, что γпр и αпр для данных сред зависят от их абсолютных показателей преломления. Это применяется на практике в приборах для измерения показателя преломления веществ – рефрактометрах.
ЛУПА И МИКРОСКОП
Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями (одна из них обычно сферическая, иногда цилиндрическая, а вторая сферическая или плоская), преломляющими световые лучи, способные формировать оптические изображения предметов. Материалом для линз служат стекло, кварц, кристаллы, пластмассы и т. п. По внешней форме линзы делятся на: 1) двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые; 6) вогнуто-выпуклые. По оптическим свойствам линзы делятся на собирающие и рассеивающие. Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше по сравнению с радиусами поверхностей, ограничивающих линзу. Формула тонкой линзы:
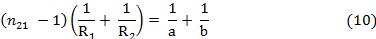
Фокусное расстояние линзы:
f = 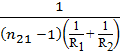 (11)
(11)
Точки F, лежащие по обе стороны линзы на расстоянии, равном фокусному, называются фокусами линзы. Фокус − это точка, в которой после преломления собираются все лучи, падающие на линзу параллельно главной оптической оси (прямая, проходящая через центры кривизны поверхностей линзы).
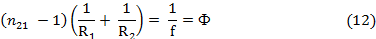
Величина Ф, рассчитываемая по формуле (12) называется оптической силой линзы. Диоптрия − оптическая сила линзы с фокусным расстоянием 1 м: 1 дптр = 1/м. Линзы с положительной силой являются собирающими, с отрицательной − рассеивающими.
Учитывая (12) формулу тонкой линзы можно записать в виде:

Микроскоп является одним из важнейших лабораторных приборов в биологических и медицинских исследованиях. Микроскоп широко применяется для наблюдений и исследования таких объектов, которые невозможно различить невооруженным глазом.
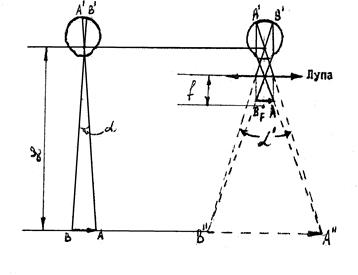
Глаз человека – сложная и совершенная оптическая система. Особенности строения глаза и получения изображения объекта на сетчатке глаза подробно разбираются в указанной литературе. В целом оптическая система глаза действует как собирающая линза с переменным фокусным расстоянием. Размер изображения на сетчатке глаза определяется углом зрения α (рис. 3а). Однако для малых (или удаленных) предметов угол зрения мал и детали предмета выявляются недостаточно.
 |
| (а) (б) Рис. 3 |
Оптические приборы, вооружающие глаз, позволяют увеличить угол зрения и поэтому более подробно различать детали предмета. Достигаемый при этом эффект характеризуется угловым увеличением Г прибора:
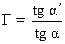 (14)
(14)
где α′ и α – углы зрения, под которым виден предмет соответственно через прибор и невооруженным глазом.
Простейшим оптическим прибором для рассматривания мелких предметов является лупа. Роль лупы выполняют также окуляры оптических приборов – микроскопа, спектроскопа, поляриметра и др.
Лупа – собирающая короткофокусная линза, которую располагают между предметом и глазом. Если невооруженным глазом рассматривать предмет АВ (рис. 3а) с расстояния наилучшего (ясного) зрения L =25 см, то он будет виден под углом α, причем
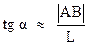
Поскольку глаз на практике располагают вблизи заднего фокуса лупы (рис. 3б), можно считать, что 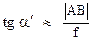 .
.
Подставив полученные значения tg α и tg α′ в формулу (1), получим выражение для углового увеличения лупы:
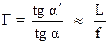 (15)
(15)
Увеличение лупы обратно пропорционально ее фокусному расстоянию и показывает, во сколько раз увеличивается линейный размер изображения на сетчатке за счет применения лупы. На практике используются лупы не бо-
лее 20 – кратного увеличения (20x). Более короткофокусные линзы дают искаженное изображение.
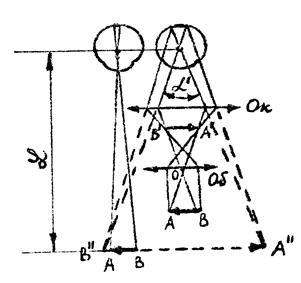
Оптическая система микроскопа состоит из объектива и окуляра, расположенных друг от друга на расстоянии 15 – 20 см на рисунке 4 схематически показан ход лучей в микроскопе.
Предмет АВ помещают чуть дальше переднего фокуса Fоб объектива Об, который дает действительное обратное и увеличенное изображение А′В′. Это промежуточное изображение попадает между окуляром Ок и его передним фокусом Fок . Его рассматривают через окуляр как через лупу. Окончательное изображение А′′В′′ получается
мнимым, увеличенным и прямым относительно А′В′, но обратным относительно самого предмета АВ. Положение объектива относительно предмета подбирается так, чтобы
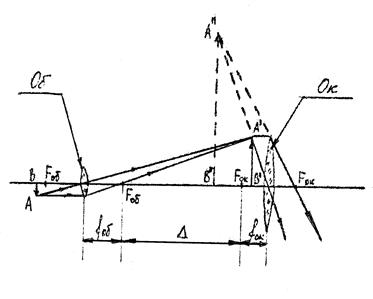 |
| Рис. 4 |
окончательное изображение А′′В′′ располагалось от глаза на расстоянии наилучшего (ясного) зрения L =25 см (рис. 5, на котором для наглядности не соблюдены относительные размеры основных параметров). Качество изображения во многом зависит от объектива. Хорошие объективы, в которых устранены недостатки, состоят из многих линз (иногда более 10), заключенных в общую оправу. Окуляр и объектив биологического микроскопа являются съемными и размещены на концах цилиндрической трубки – тубуса, укрепленного на массивном штативе. Расстояние между внутренними фокусами объектива и окуляра называется оптической длиной тубуса. Оптическая длина Δ тубуса короче его геометрической длины на сумму фокусных расстояний объектива и окуляра.
 |
| Рис. 5 |
Увеличение Г микроскопа равно произведению увеличений объектива и окуляра:
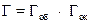 (16)
(16)
Окуляр используется как лупа, и его увеличение определяется формулой:
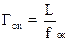 (17)
(17)
Увеличение объектива можно найти, рассматривая подобные треугольники ОАВ и ОА′В′ (см. рис. 4 и 5) и учитывая, что Δ >> fоб:
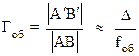 (18)
(18)
Следовательно, угловое увеличение микроскопа:
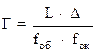 (19)
(19)
Объективы биологических микроскопов имеют угловое увеличение от 8х до 90х, окуляры – от 7х до 15х. Следовательно (см. формулу 16), угловое увеличение микроскопа лежит в пределах от 56х до 1350х. Угловое увеличение оптического микроскопа свыше 1000х использовать нецелесообразно, так как при этом ухудшается качество изображения.
Линейным или поперечным увеличением К называется отношение линейных размеров (см. рис. 5) изображения X2 = |A''B''| предмета X1 = |AB|:
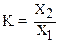 (20)
(20)
ЭЛЕМЕНТЫ ФОТОМЕТРИИ
Фотометрия – это раздел оптики, который изучает методы и приемы измерения видимого света (интервал электромагнитного излучения Δλ = 380 ÷ 760 нм).
Поток энергии, который несут световые волны, можно оценить двояко: 1) энергетически – как количество энергии, проходящей через данную поверхность в единицу времени (т. е. мощность P, измеряется в Ваттах), или 2) по зрительному ощущению. Мерой чувствительности глаза к свету различной длины волны можно характеризовать кривой видности (рис.6). Абсциссой этой кривой служат длины волн λ, а ординатой – коэффициенты видности Vλ, т. е. величины обратно пропорциональных мощностям монохроматических излучений, равноярких с точки зрения визуальной оценки. Кривая видности имеет максимум при λ = 555 нм, условно принимаемый за 1; при удалении от максимума кривая быстро убывает к 0. Так, например, для λ = 670 нм требуется мощность, примерно в 30 больше, чем для λ = 550 нм, чтобы вызвать одинаковое по силе зрительное ощущение.
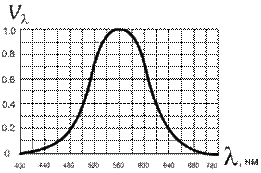 |
| Рис.6 |
В фотометрии введено понятие светового потока Ф, оценивая поток энергии света по зрительному ощущению. Световой поток монохроматического излучения (излучение с определенной длиной волны и частотой): Фλ = Pλ · Vλ. Если излучение осуществляется волнами различной длины, то световой поток такого излучения слагается из световых потоков Ф для каждой длины волны: Ф = ΣФλ = ΣPλ · Vλ. Световой поток измеряется в люменах (лм).
На пути светового потока (рис. 7), идущего от то-
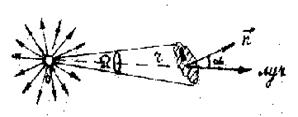 |
| Рис. 7 |
чечного источника 0 (его размеры малы по сравнению с расстоянием до места наблюдения и свет испускается равномерно по всем направлениям), на расстоянии r расположена малая площадка s, нормаль 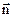 к которой составляет угол α с лучем. На площадку s от источника 0 попадает световой поток, ограниченный телесным углом Ω. Мерой телесного угла Ω служит отношение площади сферы Sсф, вырезаемой конической поверхностью на сфере произвольного радиуса r c центром в вершине 0 конической поверхности, к квадрату радиуса:
к которой составляет угол α с лучем. На площадку s от источника 0 попадает световой поток, ограниченный телесным углом Ω. Мерой телесного угла Ω служит отношение площади сферы Sсф, вырезаемой конической поверхностью на сфере произвольного радиуса r c центром в вершине 0 конической поверхности, к квадрату радиуса:
 (21)
(21)
Измеряется Ω в стерадианах (ср).
Сила света I точечного источника света (в данном направлении) равна отношению светового потока Ф к величине телесного угла Ω:
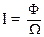 (22)
(22)
Единицей измерения силы света служит кандела (кд). В СИ кандела является основной единицей.
Освещенностью E поверхности называется величина, равная отношению светового потока Ф, падающего на данную поверхность, к ее площади s:
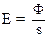 (23)
(23)
Измеряется освещенность в люксах (лк).
Освещенность в разных точках поверхности может быть различна. Для вычисления освещенности следует воспользоваться формулами (21), (22), (23):
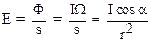 (24)
(24)
Соотношение
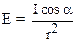 (25)
(25)
называется законом освещенности от точечного источника света.
В таблице 1 сравнивается световые и энергетические единицы фотометрических величин.
Таблица 1
| Величины | Обозначение | Едини-ца свето-вая | Символ | Единица энергетическая |
| Световой поток | Ф | люмен | лм | Ватт |
| Сила света | I | кандела | кд | Ватт/стера-диан |
| Освещенность | E | люкс | лк | Ватт/м2 |
Если источник света нельзя считать точечным, то для его характеристики в фотометрии вводятся понятия – светимость и яркость, которые характеризуют излучение единицы площади светящейся поверхности.
Яркость светящейся поверхности вычисляется по формуле:
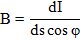 (26)
(26)
где I − сила света элемента излучающей поверхности;
s − площадь проекции элемента излучающей поверхности на плоскость, перпендикулярную направлению наблюдения;
φ − угол между направлением излучения и нормалью к площадке ds.
Светимость определяется соотношением:
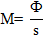 (27)
(27)
где Ф − световой поток, испускаемый поверхностью;
s − площадь этой поверхности.
Приборы, служащие для измерения световых величин, называются фотометрами. Если шкала фотометра проградуирована в единицах освещенности – люксах, прибор называется люксметром.
КОНЦЕНТРАЦИОННАЯ КОЛОРИМЕТРИЯ
Концентрационная колориметрия – это фотометрический метод определения концентрации вещества в окрашенных растворах, который связан с изменением интенсивности света.
Интенсивностью света называется отношение энергии W, переносимой светом через поверхность, перпендикулярную световому лучу, ко времени переноса t и к площади s этой поверхности:
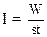 (28)
(28)
Прохождение света через вещество ведет к возбуждению колебаний электронов среды под действием электромагнитного поля световой волны. Этот процесс сопровождается потерей энергии света, которая превращается в различные формы внутренней энергии вещества или в энергию вторичного излучения, и называется поглощением света. Поглощение света, например, может приводить к нагреванию вещества, ионизации или возбуждению атомов и молекул, фотохимическим процессам и т. п.
Поглощение света веществом обычно носит избирательный (селективный) характер: свет разных длин волн поглощается по-разному. Поэтому большинство окружающих нас тел имеет «собственный» цвет. Из потока белого света тело поглощает лучи только определенных длин волн, остальные отражаются, пропускаются или рассеиваются. Так, например, листья живых растений обладают значительным поглощением во всем видимом спектре, кроме 520 нм < λ < 600 нм (зеленая часть) и λ > 700 нм (темно-красная часть).
Избирательным поглощением стекла или полиамидной пленки обусловлен парниковый эффект: значительная часть инфракрасного излучения, испускаемого нагретой землей, поглощается стеклом (или пленкой) и, таким образом, задерживается внутри парника. Слой озона в верхних слоях атмосферы интенсивно поглощает ультрафиолет и тем самым защищает живую природу на Земле от губительного действия коротковолнового излучения. Биологические ткани, клеточные структуры, отдельные органические молекулы также сильно поглощают ультрафиолетовое излучение.
Закон поглощения света однородной средой выводится на основании экспериментальных наблюдений Бугера и Ламберта: уменьшение интенсивности при поглощении света на малом пути пропорционально длине этого пути и самой интенсивности. Если выбрать небольшой слой вещества толщиной dx (рис.8а), то ослабление интенсивности dI опишется (на основе опытных данных) следующей формулой:
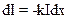 , (29)
, (29)
где k – коэффициент поглощения зависит от рода вещества и длины волны света. Знак «-» означает, что интенсивность I света уменьшается за счет его поглощения.
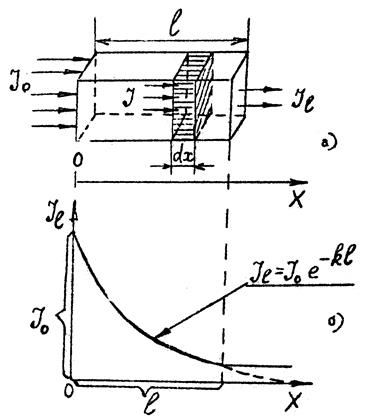 |
| Рис. 8 |
Чтобы определить полное изменение интенсивности света после его прохождения сквозь слой толщиной l, проинтегрируем уравнение (29), предварительно разделив переменные:
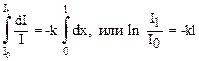
После потенцирования:
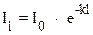 (30)
(30)
Соотношение (30) называется законом Бугера – Ламберта. При распространении света в веществе его интенсивность убывает по экспоненте (рис. 8б). В слое толщиной l = 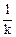 интенсивность света падает в e = 2,72 раза.
интенсивность света падает в e = 2,72 раза.
Для удобства практической оценки ослабления света при его прохождении сквозь образец пользуются понятиями:
коэффициента пропускания 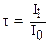 (31)
(31)
и оптической плотности 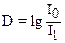 (32)
(32)
Очевидно, что 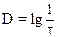 или
или 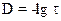 (33)
(33)
Коэффициент поглощения определяется по формуле:
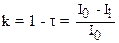 (34)
(34)
Большое практическое значение имеет поглощение света растворами. Опытным путем установлено, что для веществ, растворенных в прозрачных растворителях, коэффициент поглощения (k) пропорционален их концентрации (С) в растворе (закон Бера):
k = A · C (35)
где А – коэффициент пропорциональности, постоянный в случае слабых растворов и зависящий от рода молекул растворенного вещества (при больших С этот коэффициент начинает зависеть от С и пропорциональная зависимость k(С) нарушается).
Поглощение света растворами описывается законом Бугера – Ламберта – Бера:
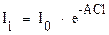 (36)
(36)
Отсюда 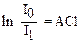 или
или 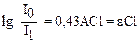 (37)
(37)
где – 0,43А = ε (молярный коэффициент поглощения, характеризует поглощение света молярным раствором исследуемого вещества в слое единичной толщины) является важной физической характеристикой растворов.
Из соотношений (37) и (32) оптическая плотность раствора определяется следующей формулой:
D = εCl (38)
Закон Бугера – Ламберта – Бера (формулы 36 и 38) лежит в основе концентрационной колориметрии и дает возможность: 1) определить концентрацию (С) вещества в растворе (при известных D и ε); 2) идентифицировать вещества(т. е. определить ε по известным D и С при облучении монохроматическим светом).
Для определения оптической плотности D растворов используют специальные приборы – колориметры. При этом фотометрирование проводят визуально или с помощью чувствительных фотоэлементов.
ВОЛНОВАЯ ОПТИКА
УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ
СТОЯЧИЕ ВОЛНЫ
Колеблющееся тело — источник колебаний (камертон, струна, мембрана и т. д.), находящееся в упругой среде, приводит в колебательное движение соприкасающиеся с ним частицы среды. Колебание этих частиц передается (силами упругости) соседним частицам среды и т. д. Через некоторое время колебание охватит всю среду. Процесс распространения колебательного движения в среде называется волной. Направление распространения волны (колебаний) называется лучом. Волна называется поперечной, если частицы среды колеблются перпендикулярно лучу. Если колебания частиц среды происходят вдоль луча, волна называется продольной.
Если точка 0 совершает колебательное движение в упругой среде по гармоническому закону (рис. 9):
у = А sin ωt, (39)
где y — смещение колеблющейся точки;
А — амплитуда (наибольшее смещение точки от положения равновесия); t — время; Т— период; ω = 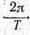 — циклическая или круговая частота. — циклическая или круговая частота. | 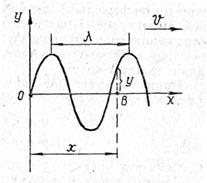 Рис.9 Рис.9 |
Соседняя точка В среды придет в. колебательное движение с некоторым запозданием на время:
τ = 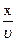 , (40)
, (40)
где х — расстояние, на которое распространилось колебание от точки 0 до точки, В;
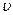 — скорость распространения колебания от 0 до В.
— скорость распространения колебания от 0 до В.
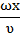 Тогда уравнение колебаний в точке В запишется:
Тогда уравнение колебаний в точке В запишется:
y = А sin ω (1—τ) = А sin (ωt − ) (41)
Соотношение (41), позволяющее определить смещение любой точки среды в любой момент времени, называется уравнением бегущей плоской синусоидальной волны.
Длиной волны(λ)называется расстояние между соседними точками, находящимися в одинаковой фазе, т. е. расстояние, пройденное волной за один период колебания, следовательно:
λ = vT = 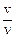 ; v = λν (42)
; v = λν (42)
где ν — частота колебания частиц среды (частота волны). Колебания частиц среды имеют ту же частоту, что и колебания источника волн. Волны, частоты колебаний в которых лежат в пределах от 16 до 20000 Гц, называют звуковыми. В звуковой или акустической волне происходят механические колебания частиц среды с малыми амплитудами.
Подставляя в уравнение (41) v= 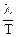 и учитывая, что ω =
и учитывая, что ω = 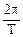 = 2πν, получим другие формы записи уравнения волны:
= 2πν, получим другие формы записи уравнения волны:
y = А sin 2π(t/T—x/λ) = А sin 2π (νt— x/λ) = А sin(ωt - 2π x/λ), (43)
где 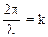 — волновое число, которое показывает, сколько длин волн укладывается на отрезке длиной 2π. Тогда уравнение волны запишется:
— волновое число, которое показывает, сколько длин волн укладывается на отрезке длиной 2π. Тогда уравнение волны запишется:
y = А sin(ω t—kx) (44)
Метод определения скорости звука основан на свойствах звуковой стоячей волны.Стоячие волны образуются при наложении (интерференции) двух встречных плоских волн с одинаковой амплитудой. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая навстречу отраженная волна, налагаясь друг на друга, дают стоячую волну.
Напишем уравнение двух плоских волн, распространяющихся вдоль оси X в противоположных направлениях:
y1= А sin (ωt—kx), у2 = А sin (ωt + kx)
Сложив эти уравнения и преобразовав результат по формуле для суммы синусов, получим:
у = y1 + у2 = 2А cos k x sin ωt (45)
Заменим волновое число kего значением 2π/λ. Тогда уравнение (45) примет вид:
у = 2Асоs 2π 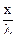 sin ωt (46)
sin ωt (46)
Уравнение (46) есть уравнение стоячей волны. Из этого уравнения видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда (у max) зависит от х:
у max = 2А cos 2π 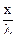
В точках, координаты которых удовлетворяют условию
| (7) |
2π 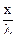 =±nπ (n = 0, 1,2, 3, ...), (47)
=±nπ (n = 0, 1,2, 3, ...), (47)
амплитуда колебаний достигает максимального значения (у max = 2А). Эти точки называются пучностямистоячей волны. Из (47) получаются значения координат пучностей:
xпучн = ± n 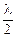 (n = 0,1,2,3,…), (48)
(n = 0,1,2,3,…), (48)
В точках, координаты которых удовлетворяют условию
2π 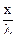 =±(n +
=±(n + 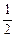 )π (n = 0, 1,2, 3, ...),'
)π (n = 0, 1,2, 3, ...),'
амплитуда колебаний обращается в ноль (у max = 0). Эти точки называются узламистоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют значения
| (9) |
xузл = ±(n + 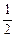 )
) 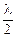 (n = 0, 1,2, 3, ...), (49)
(n = 0, 1,2, 3, ...), (49)
Из формул 48 и 49 следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно λ/2. Пучности и узлы сдвинуты друг относительно друга на λ /4.
ИНТЕРФЕРЕНЦИЯ СВЕТА
По современным научным представлениям, свет — это сложный электромагнитный процесс, обладающий как волновыми, так и корпускулярными свойствами. Настоящая работа базируется на наблюдении и изучении явления интерференции света, которое объясняется с позиций волновой теории света.
Интерференцией света называется такое сложение световых волн, в результате которого образуется устойчивая картина их усиления и ослабления.
НАЧАТЬ С → ↓
Рис. 10, формула 50
Для осуществления интерференции накладывающиеся волны должны удовлетворять условиям когерентности (согласованности по фазе световых колебаний в пучках света или отдельных частях пучка). Когерентными называются волны, имеющие одинаковые частоты и постоянную во времени разность фаз.
Реальные светящиеся тела испускают некогерентные волны. Так происходит потому, что поверхность любого светящегося тела состоит из множества точек (атомов), автономно, прерывно и случайным образом излучающих световые волны. Понятно, что никакой согласованности по фазе между такими волнами нет. Для получения когерентных световых пучков применяют различные искусственные приемы, в основе которых лежит разделение одного и того же пучка на два, идущих впоследствии к какой-либо точке пространства (экрана) двумя различными путями. В зависимости от способа разбиения пучка существует два разных метода получения когерентных «источников»:
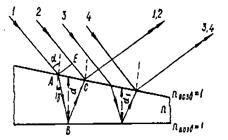 | 1) метод деления волнового фронта, когда исходящий от источника пучок делится на два, либо проходя через два близко расположенных отверстия, либо отражаясь от зеркальных поверхностей и т. д.; |
| Рис. 10 |
2) метод деления амплитуды, который предполагает деление пучка путем прохождения и отражения от полупрозрачной поверхности. Именно этот способ рассматривается в настоящем разделе; в результате чего получается интерференционная картина, называемая кольцами Ньютона.
Разделение луча (пучка) на два когерентных осуществляется путем его отражения от поверхностей тонкого прозрачного слоя (рис. 10): Пусть параллельный монохроматический пучок света от одного источника падает на клиновидный слой; выделим из него два луча — 1 и 2 (или любую другую пару лучей — 3 и 4). Проведем перпендикулярно лучам плоскость АЕ, которая является фронтом падающей волны (до плоскости АЕ два луча — 1 и 2, идущие от одного источника, дошли одновременно, а следовательно, имели нулевую разность фаз). От плоскости АЕ лучи прошли различные пути; в точке С произошло сложение колебаний, результат которого будет зависеть от разности фаз складывающихся волн.
Разность фаз связана с разностью хода δ лучей соотношением:
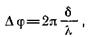 (39)
(39)
где
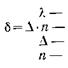 длина волны падающего света;
длина волны падающего света;
оптическая разность хода лучей;
геометрическая разность хода лучей ;
абсолютный показатель преломления
Оптическая разность хода δ лучей 1 и 2 в рассматриваемом случае выразится в виде:
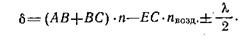 |
(40)
Член π/2 возникает соответственно «потере» фазы (запаздыванию) на π при отражении света от оптически более плотного слоя диэлектрика в оптически менее плотный. Знак плюс или минус берется в зависимости от того, где происходит указанное отражение. Очевидно, в данном случае следует взять знак минус (клин находится в воздухе, отражение от более плотной среды происходит в точке С, следовательно, «теряет» фазу отраженный луч 2). Приблизительно полагая в формуле (40) АВ = ВС = = d и ЕС=0 (поскольку падающий пучок света узкий и все лучи 1, 2, 3, 4 и т. д. практически совпадают), получаем следующее выражение для оптической разности хода:
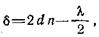 (41)
(41)
где d— толщина клина в точке В.
'Интерференционные максимумы и минимумы будут иметь такой вид:
2dn - 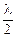 =kλ = 2k
=kλ = 2k 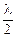 (41a максимум);
(41a максимум);
2dn - 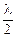 = (2k—1)
= (2k—1) 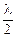 (41б минимум),
(41б минимум),
где k = 0,1,2,...— порядок интерференционного максимума и минимума.
Из формул (41) видно, что всем точкам поверхности пластинки одинаковой толщины соответствует одна и та же интерференционная картина: максимумы или минимумы одинаковой интенсивности. Интерференционная картина имеет вид полос светлых и темных, их называют полосами (линиями) равной толщины. Этот вид интерференции называется интерференцией равной толщины. В случае клиновидного слоя полосы будут параллельны ребру клина (рис. 11). При использовании белого (полихроматического) света интерференционные полосы приобретают радужную окраску (всем известны цвета тонкой масляной или керосиновой пленки на воде или на стекле). Это происходит потому, что разность хода б (формулы (41)) зависит и от длины волны, а следовательно, при одной и той же толщине пластинки dмаксимумы и минимумы для волн различных длин будут несколько сдвинуты относительно друг друга.
Интерференцию можно также наблюдать в проходящем через пластинку свете.
В зависимости от формы пластинки меняется и форма интерференционных полос. Следует заметить, что в реальных условиях падающие лучи не идеально параллельны, грани пластинки искривлены, толщина неравномерно меняется, показатель преломления тоже, меняется на неоднородностях материала и т. д. По всем этим, многочисленным причинам будут наблюдаться причудливо изогнутые линии, вид которых дает возможность судить очень точно о толщине пластинки в данной точке или о неоднородностях материала (интерференционные методы измерения — одни из самых точных).
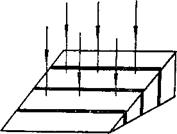 | В случае когда сферическая линза наложена на плоское стекло (рис. 3), роль пластинки переменной толщины играет воздушный слой (n возд = 1) между линзой и плоской пластинкой, а интерференционные полосы равной толщины |
| Рис. 11 |
образуют концентрические окружности с темным пятном (минимумом) в середине. Эта интерференционная схема представляет собой схему колец Ньютона.
На основании формулы (40) и следующих за ней рассуждений будем здесь иметь:
δ = 2dl + 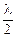 = 2d +
= 2d + 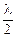 (42)
(42)
Учитывая условия (41) совместно с (42), покажем, при каких значениях d возникают светлые и темные интерференционные кольца в данной схеме:
dk = 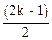
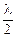 (42а, максимум)
(42а, максимум)
dk = kλ = 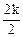
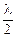 (42б, минимум)
(42б, минимум)
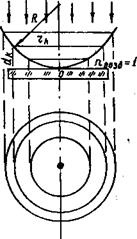
откуда и следует, что максимума нулевого порядка не будет, т. е. в отраженном свете в схеме колец Ньютона наблюдается темное пятно (рис. 12).
Длина световой волны может быть определена на основании рис. 12:
R2 = 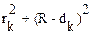 или
или
 | 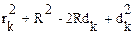 (43) Отсюда с учетом того, что толщина d невелика и член d2является пренебрежимо малым, получаем: (43) Отсюда с учетом того, что толщина d невелика и член d2является пренебрежимо малым, получаем: 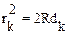 (44) Подставим в (44) значение dk (минимум) из формул (42): (44) Подставим в (44) значение dk (минимум) из формул (42): 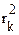 = kλR, т. е. = kλR, т. е. |
| Рис.12 |
λ = 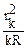 (45)
(45)
где rk— радиус интерференционного кольца — минимума k-того порядка;
R— радиус сферы линзы.
Так как обеспечить контакт в точке О (рис. 12) трудно вследствие попадания пылинок, то пользуются другой формулой, в которую входит комбинация из двух значений радиусов интерференционных колец rk и гг-, что позволяет исключать возможный зазор (т. е. реально существующее увеличение толщины всего воздушного слоя) в точке 0, Для i-того и k-того колец можно записать:
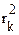 = kλR;
= kλR;
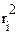 = iλR
= iλR
Вычтем почленно эти уравнения:
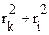 = (k - i) λR откуда
= (k - i) λR откуда
λ = 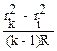 , (46)
, (46)
где k и i — порядки интерференционных колец.
Формула (46) остается одной и той же как для интерференционных минимумов, так и для максимумов.
Точность определения λ по формуле (46) зависит от того, насколько точно измерены rk и ri, а так как последние величины являются очень малыми, то для их измерения пользуются микроскопом. Кроме того, для понижения погрешности следует выбрать rk и ri таким образом, чтобы числа k и i были возможно дальше друг от друга.
ДИФРАКЦИОННАЯ РЕШЕТКА
Экспериментально установлено, что свет в однородной среде распространяется прямолинейно. Однако более детальные наблюдения показывают, что световая волна заходит в область геометрической тени, причем на границе между областями света и тени появляются максимумы и минимумы света, свидетельствующие о некотором перераспределении световой энергии на этой границе.
Огибание световой волной границ непрозрачных тел с образованием интерференционного перераспределения энергии по различным направлениям называется дифракцией света.
Дифракция — доказательство волновой природы света; дифракция свойственна не только световым, но и вообще всяким волнам. Различают с некоторой степенью условности дифракцию сферических волн (дифракция Френеля) и дифракцию плоскопараллельных волн (дифракция Фраунгофера).
Расчет и объяснение дифракции света осуществляется на основе принципа Гюйгенса-Френеля. Согласно принципу Гюйгенса, каждую точку фронта волны можно рассматривать как самостоятельный вторичный источник сферических волн. Построив огибающую всех вторичных источников, находят положение фронта волны в любой последующий момент времени, тем самым определяют направление дальнейшего распространения света. Френель дополнил принцип Гюйгенса рядом интерференционных положений; он ввел представление о когерентности вторичных волн и их интерференции. Для того чтобы определить результат дифракции в некоторой точке пространства, следует рассчитать, согласно принципу Гюйгенса-Френеля, интерференцию вторичных волн,
 |
| Рис. 13 |
попавших в эту точку от волновой поверхности (фронта волны, в случае однородной среды).
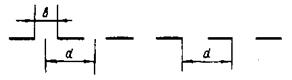
В лабораторной практике дифракционную картину чаще всего получают от дифракционных решеток. Дифракционная решетка — оптическое устройство, представляющее собой совокупность большого числа параллельных, обычно равноотстоящих друг от друга щелей одинаковой формы. Плоская прозрачная дифракционная решетка — это прозрачная пластина с большим количеством (до 1000 на длине 1 мм) тонких параллельных щелей одинаковой ширины bи равными расстояниями dмежду их серединами (или соответственными точками).Расстояние d называется периодом или постоянной решетки. Условное обозначение дифракционной решетки показано на рис. 13.
На рис. 14 представлен ход лучей через решетку согласно схеме дифракции Фраунгофера. Параллельный пучок лучей 1, идущих от одного источника, падает на дифракционную решетку 2 перпендикулярно к ней. Эти лучи дифрагируют при прохождении через решетку, образуя (вторичные) когерентные расходящиеся пучки под углами дифракции φ1, φ2,…φk. Пучки, прошедшие объектив 3 зрительной трубы, дают в его фокальной плоскости 4 дифракционную картину, как результат дошедших до плоскости 4 когерентных колебаний. Получающееся изображение можно наблюдать с помощью объектива 5.
Распределение интенсивности в дифракционной картине получим, если учтем распределение интенсивностей при дифракции от одной щели, а также взаимную интерференцию волн от всех щелей. Известно, что каждая щель (в схеме наблюдения дифракции Фраунгофера от нее) дает дифракционную картину, представленную на рис. 15. При этом условие минимумов интенсивности, называемых в данном случае первичными, выражается в виде:
 , , | (47) |
| где m=1,2,3,... (при m = 0возникает максимум); | |
| b— ширина щели |
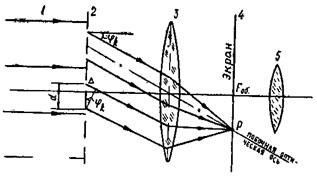 |
Рис. 14
φm— угол дифракции;
λ — длина волны в данной среде.
Условие максимумов:
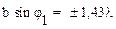 ;
; 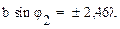 ;
;
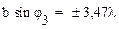 ; … (47а)
; … (47а)
При дифракции от решетки (рис. 14) картины от всех щелей придутся на одно и то же место плоскости 4 (экрана), усиливая друг друга.
Учтем взаимную интерференцию когерентных колебаний, приходящих от различных щелей. Очевидно, условие минимума (47) для одной щели является также условием минимума для решетки: в этих направлениях φ условия «гашения» света выполняются для каждой щели в отдельности, а следовательно, и для всей решетки в целом. Кроме того, из рис. 14 видно, что разность хода Δ лучей, идущих от любых соответственно расположенных пар точек (например, центральных точек) соседних щелей, равна Δ = d sin φ; если эта разность хода кратна целому числу длин волн (четному числу полуволн), то при интерференции возникнут главные максимумы, определяемые условием (2):
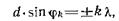 (48)
(48)
где k = 1, 2, 3, ... — порядок дифракционного максимума. Соотношение (48) называется основной формулой дифракционной решетки.
Амплитуда колебаний в точках фокальной плоскости 4 (рис. 14), соответствующих главным максимумам, равна
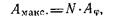 (49)
(49)
где Aφ - амплитуда колебаний, посылаемых одной щелью под утлом φ;
N - число щелей решетки.
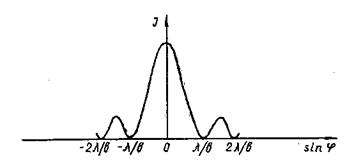 Рис. 15
Рис. 15
Известно, что интенсивность света I прямо пропорциональна квадрату амплитуды волны. Таким образом, интенсивность главных максимумов Iмакс, пропорциональна квадрату числа щелей решетки:
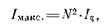 (50)
(50)
где Iφ — интенсивность, создаваемая одной щелью в направлении φ.
Можно доказать, что направления, для которых колебания от отдельных щелей взаимно погашают друг друга, т. е. добавочные минимумы удовлетворяют следующему условию:
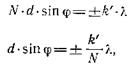
или
(k΄ = 1, 2, …, N – 1, N + 1,…)
Между двумя главными максимумами возникает (N—1) минимумов. Между этими минимумами должны находиться побочные (дополнительные) максимумы, в которых интенсивность света при достаточно большом N пренебрежимо мала по сравнению с интенсивностью главных максимумов.
Результирующее распределение интенсивности в дифракционной картине от решетки представлено на рис. 16. Пунктирная кривая дает интенсивность от одной щели, умноженную на N2. Сплошная кривая соответствует главным максимумам, а также добавочным максимумам и минимумам.
С помощью дифракционной решетки можно анализировать свет, т. е. изучать его спектральный состав. Действительно, в том случае, когда источник излучает немонохроматический свет (например, белый), то решетка разлагает его в спектр. При φ0 = 0 возникает максимум нулевого порядка, совпадающий для всех длин волн. По обе стороны от него возникнут спектры — максимумы порядков ±k. В спектре каждого порядка максимумы для более коротких волн расположатся ближе к нулевому максимуму. Максимумы для более длинных волн — дальше от него.
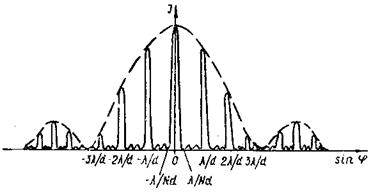 Рис. 16
Рис. 16
Способность дифракционной решетки разлагать свет в спектр позволяет использовать ее как диспергирующее устройство в спектральных приборах.
