Применение неравенства Клаузиуса к обратимым процессам. Термодинамическое определение энтропии

В случае, если термодинамический цикл состоит только из обратимых процессов, неравенство переходит в равенство Клаузиуса

,

(3.49)

имеющее принципиальное значение для построения равновесной термодинамики.

Термодинамическая энтропия S (или просто энтропия) в термодинамике является функцией состояния термодинамической системы; её существование постулируется вторым началом термодинамики. Понятие энтропии было впервые введено в 1865 году Р.Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение изменения общего количества тепла ΔQ к величине абсолютной температуры T:

dS =

Другое определение энтропии

S = k ln Z,

где Z — термодинамическая вероятность состояния или, другими словами, число микросостояний, соответствующих данному макросостоянию (число возможных изменений в мире атомов тела в данном состоянии), k = 1,3806504*10^-23Дж/К — постоянная Больцмана. Чем больше Z, тем больше хаос, т.е. энтропия - характеристика хаоса, беспорядка.

Применение неравенства Клаузиуса к необратимым процессам. Закон неубывания энтропии в изолированной системе.

Необратимый цикл Карно.В этом случае

И все равенства превращаются в неравенства

(9.28)

Уравнение (9.28) называется неравенством Клаузиуса.

Объединяя (9.27) и (9.28), получим

(9.29)

Таким образом, сумма приведенных теплот любого цикла равна нулю (обратимый процесс ) или меньше нуля (необратимый процесс).

Второй закон термодинамики – один из основных законов физики, закон о неубывания энтропии в изолированной системе.
Для системы с постоянной температурой существует определенная функция состояния S – энтропия, которая определяется таким образом, что
1. Адиабатический переход из равновесного состояния A в равновесное состояние B возможен лишь тогда, когда

.

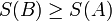2. Прирост энтропии в медленном квазистатического процессе равно

,

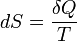где T – температура.

Расчет изменения энтропии в различных процессах. Разность энтропий двух состояний идеального газа.

Изменение энтропии нельзя непосредственно измерить, измерять можно только теплоту. Количество теплоты может быть различным в обратимом и необратимом процессе, но изменение энтропии в них должно быть одинаковым, если одинаковы начальное и конечное состояния

dS_обр. = обр.

S₂ – S₁ = dS_необр. > Þнеобр обр. > необр. (5.6)

Как и работа, теплота обратимого процесса всегда больше теплоты необ-ратимого при заданных начальном и конечном состояниях.