Теорема о циркуляции
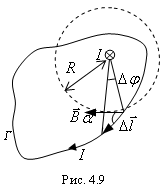 |
Существует еще одно общее соотношение, которое связывает магнитную индукцию с током. Это соотношение носит название теоремы о циркуляции вектора магнитной индукции. Пусть магнитное поле создается прямым проводником с током. Рассмотрим произвольный контур Г и зададим на нем направление обхода. Пусть 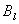 представляет проекцию вектора
представляет проекцию вектора 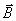 на направлении элемента
на направлении элемента 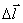 (рис. 4.9). Сумма произведений
(рис. 4.9). Сумма произведений 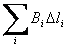
 для замкнутого контура Г называется циркуляцией вектора
для замкнутого контура Г называется циркуляцией вектора 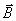 по замкнутому контуру Г. Циркуляцию проще рассчитать, когда контур совпадает с одной из силовых линий магнитного поля проводника. В этом случае вектор
по замкнутому контуру Г. Циркуляцию проще рассчитать, когда контур совпадает с одной из силовых линий магнитного поля проводника. В этом случае вектор 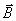 в каждой точке параллелен
в каждой точке параллелен 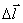 , тогда
, тогда
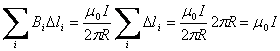 .
.
Из последнего соотношения видно, что циркуляция вектора магнитной индукции не зависит от радиуса контура.
В случае контура произвольной формы 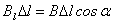 , но
, но 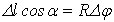 , где R – радиус окружности с центром на проводнике с током, совпадающей на малом участке с элементом контура
, где R – радиус окружности с центром на проводнике с током, совпадающей на малом участке с элементом контура 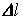 . Так как вклад в циркуляцию от элемента окружности любого радиуса одинаков, то
. Так как вклад в циркуляцию от элемента окружности любого радиуса одинаков, то
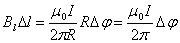
и
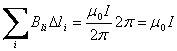 .
.
Таким образом, циркуляция вектора 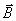 по произвольному контуру равна произведению m0 на силу тока I, пронизывающего контур, по которому берется циркуляция. Если контур не охватывает ток, то циркуляция вектора
по произвольному контуру равна произведению m0 на силу тока I, пронизывающего контур, по которому берется циркуляция. Если контур не охватывает ток, то циркуляция вектора 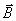 равна нулю.
равна нулю.
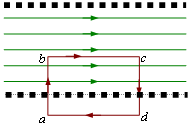 Рис. 4.10 Рис. 4.10 |
Магнитное поле соленоида. Соленоид представляет собой цилиндрическую катушку с плотно прилегающими витками. Опыт показывает, что внутри длинной катушки поле однородно и линии магнитной индукции идут параллельно ее оси (рис. 4.5б). Снаружи поле в случае бесконечно длинной катушки равно нулю. Найдем индукцию магнитного поля внутри соленоида. Для этого воспользуемся теоремой о циркуляции. На рис. 4.10. представлено сечение соленоида плоскостью, проходящей через его ось. Вычислим циркуляцию вектора индукции В по прямоугольному контуру abcd. Стороны bc и ad параллельны линиям индукции; стороны ab и cd перпендикулярны линиям магнитной индукции, и проекции вектора магнитной индукции на эти стороны равны нулю. Поэтому циркуляция вектора 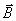 будет равна
будет равна 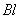 , где
, где 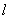 – длина стороны bc.
– длина стороны bc.
Пусть число витков соленоида на единицу его длины равно n. Тогда полный ток, который пронизывает контур, равен 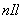 . Согласно теореме о циркуляции
. Согласно теореме о циркуляции 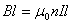 , отсюда для бесконечно длинного соленоида получим:
, отсюда для бесконечно длинного соленоида получим:
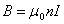 .
.
Заметим, что вблизи краев соленоида поле уже не будет однородным, и его нельзя определить по полученной формуле. Кроме того, если соленоид нельзя считать бесконечно длинным, то индукция магнитного поля вне соленоида не равна нулю.
