Ряд Фурье для гармонических сигналов
Ряд вида 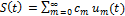 называется рядом Фурье данного сигнала. Введем основную частоту ω1=2π/T последовательности, образующей периодический сигнал. Вычисляя коэффициенты разложения запишем ряд Фурье для периодического сигнала
называется рядом Фурье данного сигнала. Введем основную частоту ω1=2π/T последовательности, образующей периодический сигнал. Вычисляя коэффициенты разложения запишем ряд Фурье для периодического сигнала 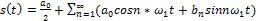 с коэф-тами
с коэф-тами
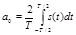
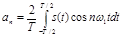
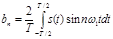
Итак, в общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами ωn = nω1 (n = 1, 2, 3, ...), кратными основной частоте последовательности. Каждую гармонику можно описать ее амплитудой An и начальной фазой φn. Для этого коэффициенты ряда Фурье следует записать в виде: an=Ancosφn, bn=Ansinφn так, что 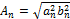 , tgφn=bn/an.
, tgφn=bn/an.
Другая, эквивалентная форма ряда Фурье: 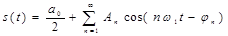
Спектральная диаграмма периодического сигнала - графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают амплитудные и фазовые спектральные диаграммы (рис. 3.2). Здесь по горизонтальной оси в некотором масштабе отложены частоты гармоник, а по вертикальной оси представлены их амплитуды и начальные фазы. 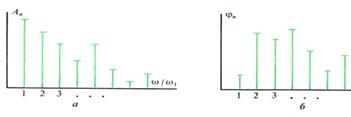
Рис.3. 2. Спектральные диаграммы некоторого периодического сигнала: а — амплитудная; б — фазовая
Особо интересуются амплитудной диаграммой, которая позволяет судить о процентном содержании тех или иных гармоник в спектре периодического сигнала. Спектральное разложение периодического сигнала можно выполнить, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:
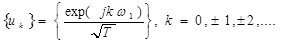
Легко видеть, что функции этой системы периодичны с периодом Т и ортонормированы на отрезке времени [—Т/2, Т/2], так как