Элементы классической теории электропроводности металлов

СОДЕРЖАНИЕ

ЦЕЛЬ РАБОТЫ……………………………………………………………………..4

ОБОРУДОВАНИЕ………………………………………………………………….4

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. Электрический ток в металлах и полупроводниках…………………………...5

1.1. Элементы классической теории электропроводности металлов……………5

1.2. Элементы зонной квантовой теории твердых тел……………………………8

1.3. Элементы квантовой теории электропроводности металлов……………….13

1.4. Элементы квантовой теории электропроводности полупроводников……..16

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

1. Описание экспериментальной установки……………………………………...21

2. Подготовка к работе на экспериментальной установке………………………24

3. Снятие температурных зависимостей сопротивлений

металла 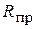и полупроводника 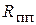……………………………………………..25

4. Обработка результатов измерений……………………………………………..25

4.1. Дополнительные вычисления………………………………………………...25

4.2. Построение графиков………………………………………………………….26

4.3. Нахождение температурного коэффициента сопротивления

металла 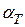………………………………………………………………………….27

4.4. Определение ширины запрещенной зоны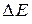

собственного полупроводника…………………………………………………….28

КОНТРОЛЬНЫЕ ВОПРОСЫ ……………………………………………………..29

БИБЛИОГРАФИЧЕСКИЙ СПИСОК……………………………………………..31

ЦЕЛЬ РАБОТЫ: изучение теоретических моделей, объясняющих зависимости сопротивлений металла и полупроводника от температуры; проведение экспериментальной проверки моделей; графическое представление полученных зависимостей; определение параметров полупроводника (ширины запрещенной зоны полупроводника 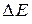) и металла (температурного коэффициента сопротивления металла ).

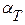ОБОРУДОВАНИЕ

1. Миниблок Исследование температурной зависимости сопротивления металла 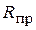и полупроводника ».

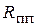2. Миниблок «Ключ».

3. Наборное поле, состоящее из контактных гнезд.

4. Регулируемый источник постоянного напряжения « 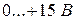» на плате «Блок генераторов».

5. «Блок мультиметров».

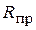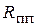6. Кабель, для подсоединения термопары миниблока «Исследование температурной зависимости и »к мультиметру, работающему в режиме измерения температуры.

7. Красные и синие соединительные провода.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Электрический ток в металлах и полупроводниках

Элементы классической теории электропроводности металлов

Американские физики Р. Толмен и Т. Стюарт в 1916 году экспериментально доказали, что носителями электрического тока в металлах являются свободные электроны. Наличие в металлах свободных электронов объясняется тем, что при образовании кристаллической решетки валентные электроны, слабее других связанные с ядрами атомов, покидают отдельные атомы. Эти электроны обобществляются кристаллической решеткой металла и могут перемещаться по его объему практически свободно. Именно такие электроны являются носителями тока и называются электронами проводимости.

Если каждый атом покинет один электрон, то концентрация электронов проводимости 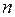(число электронов в единице объема) будет равна количеству атомов в единице объема металла. В этом случае концентрация электронов проводимости 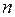будет иметь значение порядка 10²⁸¸10²⁹ м^-3.

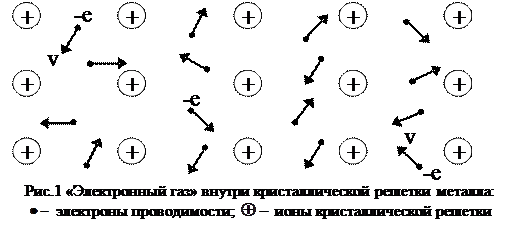
Опираясь на представление о почти свободных электронах, немецкий физик П. Друде создал классическую теорию электропроводности металлов, которая впоследствии была развита голландским физиком Х. Лоренцом. По этой теории электроны проводимости ведут себя подобно молекулам идеального газа, хаотически движущимся внутри кристаллической решетки, в узлах которой находятся положительные ионы металла (рис. 1). В отличие от молекул газа электроны в основном сталкиваются не друг с другом, а с ионами решетки. Эти столкновения приводят к установлению теплового равновесия между «электронным газом» и решёткой. Между соударениями молекулы «электронного газа» движутся свободно, проходя в среднем расстояние 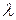, называемое средней длиной свободного пробега.

v

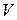При появлении в металлическом проводнике электрического поля на хаотическое тепловое движение электронов проводимости, происходящее со средней скоростью , накладывается их упорядоченное движение вдоль проводника со средней скоростью 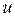, то есть возникает электрический ток.

Сравнительная оценка показала, что средняя скорость хаотического теплового движения электронов 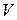примерно в 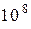раз больше средней скорости упорядоченного движения 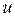. Это означает, что электроны, быстро двигаясь хаотически, медленно смещаются по проводнику под действием электрического поля (рис. 2). Такое движение электронов подобно движению молекул газа, заключенного в трубу, между концами которой поддерживается небольшая разность давлений: молекулы газа, быстро двигаясь хаотически, медленно дрейфуют вдоль трубы. Поэтому скорость упорядоченного движения 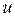называют еще скоростью дрейфаэлектронов проводимости.

Закон Ома. Рассматриваемый закон был экспериментально открыт для металлических проводников немецким физиком Г. Омом в 1826 году. Запишем этот закон в дифференциальной (локальной) форме:

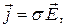(1)

где 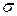- коэффициент пропорциональности между плотностью тока 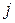и напряженностью поля в проводнике 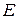, то есть удельная электропроводность металла.

Удельная электрическая проводимость металла определяется его свойствами:

,

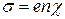(2)

где 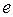- величина заряда электрона; 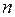- концентрация электронов проводимости; 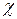- подвижность электрона.

Подвижностью электрона 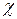называют коэффициент пропорциональности между скоростью упорядоченного движения электрона и напряженностью поля в проводнике:

.

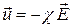(3)

Численно подвижность носителя тока (электрона) равна скорости его упорядоченного движения в электрическом поле с напряженностью, равной 1 В/м. В СИ подвижность носителей тока 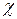измеряется в .

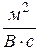Учитывая связь удельной электропроводности 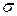с удельным сопротивлением 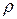проводника

,

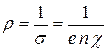(4)

можно сделать вывод о том, что величина 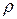определяется концентрацией носителей тока и их подвижностью. Выясним, как меняются концентрация и подвижность носителей тока у металла и полупроводника с изменением температуры. При этом мы будем опираться на квантовую теорию твердого тела, так как классическая теория оказалась не способной правильно объяснить температурную зависимость сопротивления металлов.

Температурная зависимость сопротивления металлов. Опыт показывает, что в довольно широком температурном интервале удельное сопротивление r металлов с ростом температуры увеличивается по линейному закону

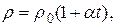(5)

где 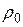– удельное сопротивление при 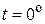С; 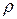– удельное сопротивление при данной температуре 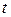по шкале Цельсия; 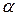– температурный коэффициент сопротивления.

График зависимости (5) представлен на рис. 3.

Для чистых металлов температурные коэффициенты сопротивления мало отличаются друг от друга и примерно равны 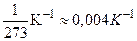. Температурный коэффициент сопротивления сплавов, как правило, существенно меньше, чем у чистых металлов. Вследствие малости коэффициента 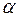удельное сопротивление 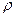металлов сравнительно слабо зависит от температуры 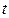. Поэтому на графике (рис. 3) зависимость (5) изображена прямой с относительно небольшим наклоном.

Из школьного курса физики известно, что от температурной зависимости для удельного сопротивления можно перейти к аналогичной температурной зависимости для сопротивления металлического проводника:

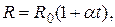(6)

где 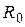– сопротивление проводника при .

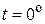Из классической теории электропроводности следует, что с увеличением температуры удельное сопротивление металлов должно возрастать пропорционально 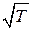. Этот вывод классической теории противоречит опытным фактам, согласно которым с увеличением температуры 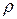возрастает пропорционально 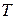. Затруднений классической теории электропроводности металлов можно избежать лишь в квантовой теории твердого тела.