Фізичні властивості напівпровідників 1 страница
В методичних вказівках до теми «Фізичні властивості напівпровідників» наведені необхідні теоретичні відомості і приклади розв’язання завдань з даної теми. Завдання напрямлені на поглиблення і закріплення теоретичних знань з таких розділів навчальної програми дисципліни «Електронні прилади»: основи зонної теорії напівпровідників; власні і домішкові напівпровідники; основи статистики часток; розподіл Фермі-Дірака; рівень Фермі у власному і домішковому напівпровідниках; залежність рівня від концентрації домішок і температури; концентрація рухомих носіїв заряду у власному і домішковому напівпровідниках і умови виродження цих напівпровідників; стан термодинамічної рівноваги; струми в напівпровідниках; дифузійний, дрейфовий та тепловий рух вільних носіїв заряду; рухливість електронів і дірок; залежність рухливості від температури і концентрації домішок; дрейфовий і дифузійний струми в напівпровіднику; електропровідність напівпровідників.
2.1. Основи зонної теорії
Атом складається з позитивно зарядженого ядра, навколо якого обертаються електрони. Орбіти електронів віддалені від ядра на різні відстані і групуються в електронні оболонки. Найбільш слабко зв’язані з ядром електрони зовнішньої, валентної оболонки. Ці електрони забезпечують поєднання атомів в кристалічній решітці. Вони вступають в ковалентний, парно-електронний зв’язок з сусідніми атомами. Енергія електрона, який рухається по орбіті, форма, розміри та орієнтація орбіти в просторі визначаються комбінацією чотирьох квантових чисел: головним квантовим числом 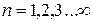 , де
, де 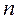 – визначається номером хімічного елементу в таблиці Менделєєва; орбітальним квантовим числом
– визначається номером хімічного елементу в таблиці Менделєєва; орбітальним квантовим числом 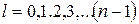 ; орбітальним магнітним квантовим числом
; орбітальним магнітним квантовим числом 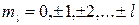 ; спіновим магнітним квантовим числом
; спіновим магнітним квантовим числом 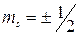 .
.
Згідно з принципом заборони Паулі, ніякі два електрона в атомі не можуть мати тих самих значень чотирьох квантових чисел. На орбіті, яка характеризується певним енергетичним рівнем і формою та визначається першими трьома квантовими числами, може бути не більше двох електронів з протилежними спінами. Таким чином окремо взятий атом речовини характеризується деяким дискретним енергетичним спектром, кількість енергетичних рівнів якого визначається головним квантовим числом (рис. 1.а).
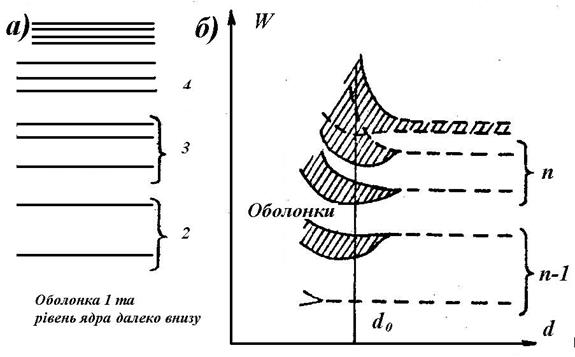
Рис. 1. Електронні оболонки атомів
В твердому тілі атоми розташовані близько (для кремнія 5·1022 атомів в одному кубічному сантиметрі) і з-за взаємного впливу атомів енергетичні рівні розщеплюються в зони. В першу чергу це характерно для енергетичних рівнів зовнішньої оболонки. Лінійчастий спектр окремого атома в твердому тілі перетворюється в зонний, в якому дозволені енергетичні зони розділені забороненими (рис.1.б). По осі абсцис відкладена міжатомна відстань, 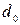 - відстань між атомами даної речовини. Кристал з відстанню
- відстань між атомами даної речовини. Кристал з відстанню 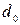 характеризується зонною енергетичною діаграмою.
характеризується зонною енергетичною діаграмою.
Електрофізичні властивості твердого тіла визначаються характером розташування і станом двох верхніх енергетичних зон. Електропровідність твердого тіла можлива тоді, коли електрон може переходити на найближчий енергетичний рівень, тобто для провідності потрібні вільні (незайняті) енергетичні рівні. Такі рівні завжди є у верхній дозволеній зоні, яка називається зоною провідності. Зона провідності – це діапазон дозволених енергетичних рівнів, які можуть займати вільні електрони провідності. Нижча енергетична зона називається валентною. Валентна зона – це діапазон енергій, які можуть займати валентні електрони в ковалентних зв’язках. Зонна структура твердих тіл при нульовій температурі Кельвіна лежить в основі класифікації металів, напівпровідників та діелектриків.
У діелектриків і напівпровідників при  електропровідність відсутня. Вільних електронів провідності немає. Всі електрони валентної оболонки утримуються в атомах ковалентними зв’язками. В зонній моделі це означає, що зона провідності порожня, а валентна зона повністю заповнена.
електропровідність відсутня. Вільних електронів провідності немає. Всі електрони валентної оболонки утримуються в атомах ковалентними зв’язками. В зонній моделі це означає, що зона провідності порожня, а валентна зона повністю заповнена.
У металів ці зони перекриваються і при нульовій температурі в зоні провідності є електрони і має місце електропровідність (рис.2).
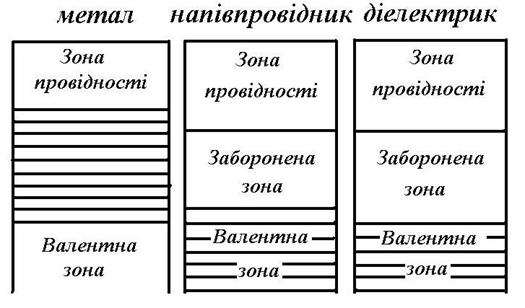
Рис. 2. Розміщення зон в різних матеріалах
Нижній енергетичний рівень зони провідності позначається 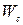 і називається дном зони провідності. Верхній енергетичний рівень валентної зони позначається
і називається дном зони провідності. Верхній енергетичний рівень валентної зони позначається 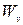 і називається стелею валентної зони. Між енергетичними рінями розташована заборонена зона
і називається стелею валентної зони. Між енергетичними рінями розташована заборонена зона 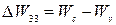 , ширина якої складає для напівпровідників десяті долі - одиниці електрон-вольт. На енергетичних зонних діаграмах енергія по осі ординат відкладається в Дж, або еВ: 1 еВ=1,602∙10-19 Дж.
, ширина якої складає для напівпровідників десяті долі - одиниці електрон-вольт. На енергетичних зонних діаграмах енергія по осі ординат відкладається в Дж, або еВ: 1 еВ=1,602∙10-19 Дж.
2.2. Концентрація носіїв заряду
В зоні провідності максимальна кількість електронів не може перевищувати подвоєної кількості дозволених енергетичних рівнів, бо за принципом Паулі на кожному рівні може знаходитися не більше двох електронів. Ймовірність знаходження електрона на енергетичному рівні 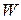 визначається температурою
визначається температурою  . При
. При 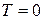 К зона провідності порожня, із збільшенням температури вона заповнюється електронами. Для визначення концентрації вільних електронів провідності застосовується функція густини енергетичних станів – це число рівнів
К зона провідності порожня, із збільшенням температури вона заповнюється електронами. Для визначення концентрації вільних електронів провідності застосовується функція густини енергетичних станів – це число рівнів 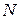 в одиниці об’єму твердого тіла, віднесених до енергії рівня
в одиниці об’єму твердого тіла, віднесених до енергії рівня 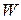 .
. 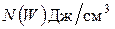 :
:
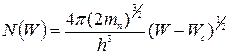 ,
,
де 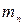 – ефективна маса електрона,
– ефективна маса електрона, 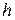 - постійна Планка,
- постійна Планка, 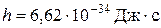 ,
, 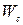 - енергія дна зони провідності,
- енергія дна зони провідності, 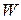 - поточне значення енергії в зоні провідності.
- поточне значення енергії в зоні провідності.
Ймовірність того, що енергетичний рівень 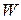 зони провідності при даній температурі
зони провідності при даній температурі  зайнятий електроном, визначається функцією Фермі-Дірака:
зайнятий електроном, визначається функцією Фермі-Дірака:
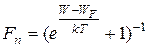
де 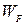 – енергія, яка називається рівнем Фермі,
– енергія, яка називається рівнем Фермі, 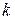 - постійна Больцмана,
- постійна Больцмана, 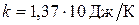 ,
,  - абсолютна температура. При будь-яких температурах рівень Фермі, це такий рівень, ймовірність заповнення, якого дорівнює 1/2. Рівень фермі – це найвища енергія частки ( в даному випадку електрона) в системі при будь-яких значеннях температури.
- абсолютна температура. При будь-яких температурах рівень Фермі, це такий рівень, ймовірність заповнення, якого дорівнює 1/2. Рівень фермі – це найвища енергія частки ( в даному випадку електрона) в системі при будь-яких значеннях температури.
В електроніці зручніше виражати енергію не в джоулях, а в електрон-вольтах, або просто в вольтах, тоді зонна енергетична діаграма напівпровідника називається потенціальною діаграмою. Поділивши енергії 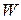 і
і 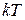 на заряд електрона
на заряд електрона  функція Фермі-Дірака набуде вигляду:
функція Фермі-Дірака набуде вигляду:
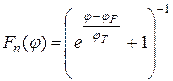 ,
,
де 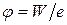 ,
, 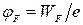 – рівень фермі у вольтах,
– рівень фермі у вольтах, 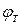 - температурний потенціал,
- температурний потенціал, 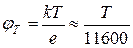 В. Значення температури підставляється в Кельвінах
В. Значення температури підставляється в Кельвінах
Концентрація вільних електронів в зоні провідності визначається інтегралом
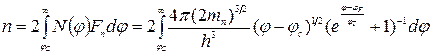 .
.
В загальному вигляді цей інтеграл не має рішення. Отримати таке рішення можливо для невироджених напівпровідників, для яких статистика Фермі-Дірака спрощується. Для невироджених напівпровідників рівень Фермі лежить завжди в забороненій зоні. Якщо розташування рівня Фермі по відношенню до дна зони або стелі валентної зони визначається нерівностями 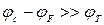 та
та 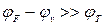 , то статистика Фермі-Дірака спрощується.
, то статистика Фермі-Дірака спрощується.
Для n–напівпровідника це статистика Максвела-Больцмана
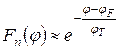 .
.
Для невироджених напівпровідників розв’язок інтеграла має вигляд
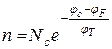 ,
,
де  - концентрація вільних електронів в зоні провідності,
- концентрація вільних електронів в зоні провідності, 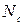 - ефективна густина станів у зоні провідності.
- ефективна густина станів у зоні провідності.
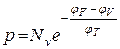
де  – концентрація вільних дірок у валентній зоні,
– концентрація вільних дірок у валентній зоні, 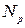 - ефективна густина станів в валентній зоні.
- ефективна густина станів в валентній зоні.
По суті 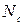 - це максимально можлива концентрація електронів в зоні провідності у невиродженому напівпровіднику за умови
- це максимально можлива концентрація електронів в зоні провідності у невиродженому напівпровіднику за умови 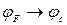 , а
, а 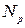 – максимально можлива концентрація дірок у валентній зоні в невиродженому напівпровіднику за умови
– максимально можлива концентрація дірок у валентній зоні в невиродженому напівпровіднику за умови 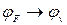 . У власних напівпровідниках рівень Фермі лежить в забороненій зоні поблизу її середини. В домішкових невироджених напівпровідниках рівень Фермі із збільшенням концентрації наближається в напівпровідниках з електронною провідністю до дна зони провідності
. У власних напівпровідниках рівень Фермі лежить в забороненій зоні поблизу її середини. В домішкових невироджених напівпровідниках рівень Фермі із збільшенням концентрації наближається в напівпровідниках з електронною провідністю до дна зони провідності 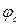 , з дірковою – до стелі валентної зони
, з дірковою – до стелі валентної зони 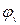 .
.
Для власного напівпровідника, для якого концентрація вільних електронів дорівнює концентрації дірок 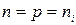 і звідки
і звідки 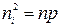 . Концентрація
. Концентрація  визначається:
визначається:
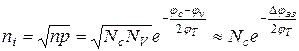 .
.
З виразу видно, що концентрація носіїв у власному напівпровіднику сильно залежить від температури, а також від ширини забороненої зоні  .
.
Значення  і
і 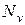 можуть бути приблизно обчислені за виразами:
можуть бути приблизно обчислені за виразами:
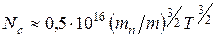 ,
,
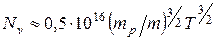 ,
,
де 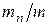 ,
, 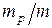 - ефективні маси електрона, дірки по відношенню до маси вільного електрона.
- ефективні маси електрона, дірки по відношенню до маси вільного електрона.
В напівпровіднику з електронною провідністю вільних електронів провідності набагато більше, ніж дірок. Електрони є основними рухливими носіями заряду і їх концентрація позначається 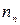 – концентрація електронів
– концентрація електронів  в шарі
в шарі  , дірки є неосновними носіями і їх концентрація позначається
, дірки є неосновними носіями і їх концентрація позначається 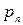 - концентрація дірок
- концентрація дірок  в шарі
в шарі  . Концентрація електронів в n–напівпровіднику визначається як
. Концентрація електронів в n–напівпровіднику визначається як
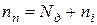 ,
,
де  – концентрація донорної домішки,
– концентрація донорної домішки, 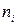 - власна концентрація електронів. Донорні домішки в робочому діапазоні температур напівпровідників іонізовані, тобто всі донори віддали електрони і перетворились в нерухомі позитивні іони
- власна концентрація електронів. Донорні домішки в робочому діапазоні температур напівпровідників іонізовані, тобто всі донори віддали електрони і перетворились в нерухомі позитивні іони  . Для типових концентрацій
. Для типових концентрацій 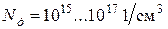 і
і 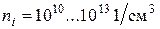 концентрація електронів визначається концентрацією донорів
концентрація електронів визначається концентрацією донорів 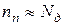 . При сталій температурі електропровідність напівпровідника залишається незмінною, тобто кількість рухливих носіїв заряду теж незмінна. Це можливо тільки при умові, коли швидкість генерації носіїв дорівнює швидкості їх рекомбінації. Це умова термодинамічної рівноваги. Вона виконується для будь-якого напівпровідника – з електронною, дірковую або власною провідністю.
. При сталій температурі електропровідність напівпровідника залишається незмінною, тобто кількість рухливих носіїв заряду теж незмінна. Це можливо тільки при умові, коли швидкість генерації носіїв дорівнює швидкості їх рекомбінації. Це умова термодинамічної рівноваги. Вона виконується для будь-якого напівпровідника – з електронною, дірковую або власною провідністю.
Умова термодинамічної рівноваги для n–напівпровідника 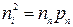 .
.
Звідки визначається концентрація неосновних носіїв дірок 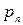 в n-напівпровіднику
в n-напівпровіднику  .
.
Аналогічні співвідношення характеризують і дірковий напівпровідник. Концентрація основних носіїв – дірок 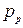 визначається як
визначається як
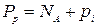 ,
,
де 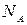 - концентрація акцепторної домішки,
- концентрація акцепторної домішки, 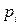 - власна концентрація дірок. Концентрація неосновних носіїв електронів
- власна концентрація дірок. Концентрація неосновних носіїв електронів  в шарі p позначається
в шарі p позначається 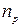 і її величина знаходиться з умови термодинамічної рівноваги
і її величина знаходиться з умови термодинамічної рівноваги  –напівпровідника
–напівпровідника
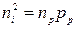 ,
, 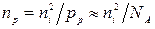 .
.
2.3. Струми в напівпровіднику
Напрямлений рух носіїв заряду в напівпровіднику, обумовлений дрейфом носіїв, виникає під дією градієнта потенціалу в електричному полі і дифузією, яка виникає під дією градієнта концентрації вільних носіїв. Повна густина струму, створеного електронами та дірками, має чотири складові: дрейфову (др.) і дифузійну (диф) для електронів і дірок
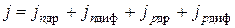 .
.
Густина дрейфових складових струму в одномірному випадку визначається як:
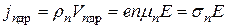 ,
,
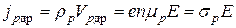 ,
,
де 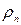 ,
, 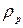 - питомі об’ємні заряди вільних електронів і дірок;
- питомі об’ємні заряди вільних електронів і дірок; 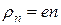 ,
, 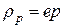 ;
;  і
і  - концентрації електронів і дірок;
- концентрації електронів і дірок; 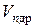 - дрейфова швидкість електронів;
- дрейфова швидкість електронів; 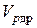 - дрейфова швидкість дірок;
- дрейфова швидкість дірок; 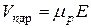 ,
, 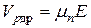 ,
, 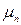 і
і 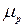 – рухливість електронів і дірок;
– рухливість електронів і дірок; 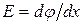 - градієнт потенціалу в електричному полі;
- градієнт потенціалу в електричному полі; 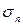 - питома провідність, створена електронами;
- питома провідність, створена електронами; 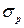 - питома провідність, створена дірками.
- питома провідність, створена дірками.
Рухливість вільних носіїв заряду – це їх середня напрямлена швидкість в електричному полі з напруженістю 1 В/см. При напрямленому русі вільних носіїв заряду в електричному полі вони взаємодіють (розсіюються) з кристалічною решіткою напівпровідника, іонною решіткою домішків, з дислокаціями, взаємодіють між собою, тобто змінюється їх напрям руху і кінетична енергія. Рухливість носіїв буде тим більшою, чим більший середній час вільного пробігу носіїв між взаємодіями. Збільшення температури напівпровідника і концентрації домішок зменшує середній час між взаємодіями, а отже зменшує рухливість електронів і дірок.
Зміна рухливості від температури визначається емпіричною залежністю:
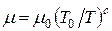 ,
,
де 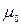 – рухливість при
– рухливість при  ; для електронів і дірок кремнію
; для електронів і дірок кремнію 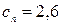 ;
; 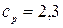 ; для електронів та дірок германію
; для електронів та дірок германію 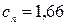 ;
; 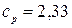 .
.
Залежність рухливості від температури визначається емпіричним виразом:
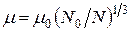 ,
,
де 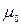 відповідає концентрації
відповідає концентрації 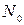 .
.
При концентраціях домішок в межах від нульової до 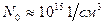 рухливість практично залишається незмінною. При значенні рухливості для
рухливість практично залишається незмінною. При значенні рухливості для 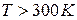 і
і 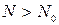 необхідно спочатку визначити рухливість для заданої концентрації домішок і температури
необхідно спочатку визначити рухливість для заданої концентрації домішок і температури  , рухливості при цьому зменшаться. Далі необхідно для нових значень рухливості розрахувати, як вони зменшаться під впливом температури
, рухливості при цьому зменшаться. Далі необхідно для нових значень рухливості розрахувати, як вони зменшаться під впливом температури 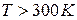 .
.
Густина дифузійних складових струму в одномірному випадку визначається як
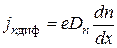 ,
, 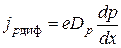 ,
,
де 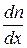 ,
, 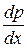 – градієнти концентрації вільних носіїв, і
– градієнти концентрації вільних носіїв, і 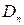 ,
, 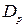 коефіцієнти дифузії електронів і дірок, пов’язані з рухливостями формулою Ейнштейна
коефіцієнти дифузії електронів і дірок, пов’язані з рухливостями формулою Ейнштейна 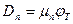 ,
, 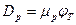 .
.
Коефіцієнти дифузії також залежать від температури і концентрації домішок через залежність рухливості від цих змінних
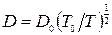 ,
, 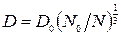 .
.
З урахуванням всіх складових густина повного струму має вираз
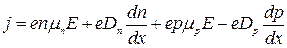 .
.
Електронні і діркові дифузійні складові створюють спільний струм одного напряму. Мінус у виразі 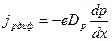 пояснюється тим, що дірки (позитивні заряди) рухаються від більшої концентрації до меншої (рис.3), тобто в цьому випадку градієнт
пояснюється тим, що дірки (позитивні заряди) рухаються від більшої концентрації до меншої (рис.3), тобто в цьому випадку градієнт 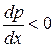 . За напрям струму в техніці прийнятий напрям руху позитивних зарядів. Щоб напрям струму створений дірками був позитивний у виразі
. За напрям струму в техніці прийнятий напрям руху позитивних зарядів. Щоб напрям струму створений дірками був позитивний у виразі 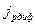 ставиться мінус.
ставиться мінус.

Рис. 3. Градієнт концентрації дірок в напівпровіднику
Питома провідність напівпровідника, створена електронами і дірками визначається як 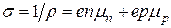 , де
, де 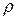 – питомий опір.
– питомий опір.
Оскільки  ,
,  ,
, 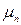 і
і 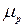 залежать від температури і концентрації домішок, то й питома провідність і питомий опір також залежать від цих змінних.
залежать від температури і концентрації домішок, то й питома провідність і питомий опір також залежать від цих змінних.
Рівень (потенціал) Фермі залежить від температури і концентрації домішок. Потенціал Фермі на потенціальній діаграмі невиродженого напівпровідника може бути відрахований від потенціалу дна зони провідності 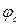 , потенціалу стелі валентної зони
, потенціалу стелі валентної зони 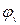 або від потенціалу середини забороненої зони
або від потенціалу середини забороненої зони 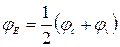 .
.
Для електронного напівпровідника
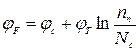 ,
, 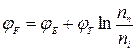 .
.
Для діркового напівпровідника
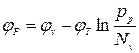 ,
, 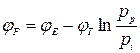 .
.
В цих виразах 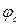 ,
, 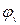 – електричні потенціали, а
– електричні потенціали, а 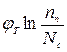 ,
, 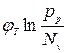 – хімічні потенціали. В загальному вигляді потенціал Фермі є алгебраїчною сумою електричного і хімічного потенціалів. Наявність градієнту електричного потенціалу характеризує можливість дрейфу вільних носіїв заряду, наявність градієнту хімічного потенціалу, тобто градієнту концентрації вільних носіїв, характеризує можливість дифузії вільних носіїв заряду.
– хімічні потенціали. В загальному вигляді потенціал Фермі є алгебраїчною сумою електричного і хімічного потенціалів. Наявність градієнту електричного потенціалу характеризує можливість дрейфу вільних носіїв заряду, наявність градієнту хімічного потенціалу, тобто градієнту концентрації вільних носіїв, характеризує можливість дифузії вільних носіїв заряду.
Якщо існує градієнт потенціалу Фермі, то це означає, що існує напрямлений рух носіїв заряду в напівпровіднику. В умовах рівноважного стану напівпровідника, коли напрямленого руху носіїв заряду нема, це означає, що 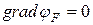 і на потенціальних діаграмах
і на потенціальних діаграмах 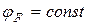 , тобто «горизонтальний», хоча в рівноважному стані можуть бути градієнти електричного і хімічного потенціалів, тобто відповідно діркові і дифузійні струми. Ці струми взаємно врівноважуються і сумарний струм дорівнює нулю.
, тобто «горизонтальний», хоча в рівноважному стані можуть бути градієнти електричного і хімічного потенціалів, тобто відповідно діркові і дифузійні струми. Ці струми взаємно врівноважуються і сумарний струм дорівнює нулю.
2.4. Приклади розв’язання задач розділу «Фізичні властивості напівпровідників»
Задача 2.1.1.
Обчислити положення рівня Фермі 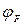 відносно дна зони провідності
відносно дна зони провідності 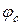 при температурі 400 К для кристалу кремнію з концентрацією донорних домішок
при температурі 400 К для кристалу кремнію з концентрацією донорних домішок 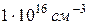 .
.
Розв’язання.
Потенціальна діаграма напівпровідника з електронною провідністю має вигляд приведений на рис.4. Необхідно визначити значення  .
.
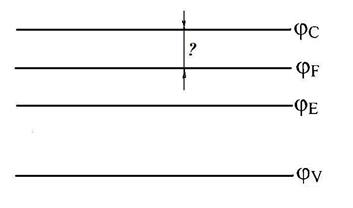
Рис. 4. Потенціальна діаграма напівпровідника з електронною провідністю
Рівень Фермі відносно дна зони провідності визначається залежністю 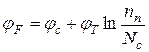 ,
,
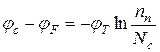 .
.
В невиродженому напівпровіднику з електронною провідністю концентрація електронів  менша ніж максимально можлива концентрація електронів в зоні провідності
менша ніж максимально можлива концентрація електронів в зоні провідності  , тобто
, тобто 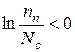 і рівень Фермі розташований нижче
і рівень Фермі розташований нижче 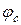 .
.
