Дифракция рентген-х лучей в кристаллах. Методы исслед дифракции: способы Лауэ, Брэгга и Дебая-Шерера

Дифракция рентгеновских лучей, рассеяние рентгеновских лучей кристаллами, при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества; направление и интенсивность вторичных пучков зависят от строения рассеивающего объекта.

Дифрагированные пучки составляют часть всего рассеянного веществом рентгеновского излучения. Наряду с рассеянием без изменения длины волны наблюдается рассеяние с изменением длины волны — так называемое комптоновское рассеяние.

Кристалл является естественной трёхмерной дифракционной решеткой для рентгеновских лучей, т.к. расстояние между рассеивающими центрами (атомами) в кристалле одного порядка с длиной волны рентгеновских лучей (~1Å=10-8 см). Дифракция рентгеновских лучей на кристаллах можно рассматривать как избирательное отражение рентгеновских лучей от систем атомных плоскостей кристаллической решётки (определяется условием Брэгга-Вульфа). Направление дифракционных

максимумов удовлетворяет одновременно трём условиям:

a (cos a — cos a0) = Нl,

b (cos b — cos b0) = Kl,

с (cos g — cos g0) = Ll.

Здесь а, b, с — периоды кристаллической решетки по трём её осям; a0, b0, g0 — углы, образуемые падающим, а a, b, g — рассеянным лучами с осями кристалла; l — длина волны рентгеновских лучей, Н, К, L — целые числа. Эти уравнения называются уравнениями Лауэ.

Метод Лауэ (1912 г.) относится к методам первой группы (угол падения на кристалл постоянен, но меняется λ). Состоит в следующем: на кристалл, ориентированный под определённым углом по отношению к лучу, падает пучок непрерывного излучения (такое излучение имеет сплошной спектр). Найдётся такая длина волны, которая удовлетворяет условию Вульфа-Брэгга.

Метод вращения (Брэгга) относится ко 2 типу (λ постоянна, меняется угол падения). Он заключается в том, что монокристалл вращают вокруг определенной оси, перпендикулярной падающему монохроматическому пучку так, что различные плоскости кристалла последовательно становятся в положение, соответствующее условию дифракции.

Метод Дебая-Шерера заключается в том, что поликристалл, состоящий из монокристаллических зёрен, освещается монохроматическим излучением. В множестве произвольно ориентированных монокристаллов всегда находятся такие, ориентировка которых отвечает условию Вульфа-Брэгга.

6. Понятие волн де Бройля. Уравнения де Бройля.

Формула де Бройля устанавливает зависимость длины волны λ, связанной с движущейся частицей вещества, от импульса p частицы: 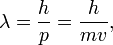где m — масса частицы, v — ее скорость, h — постоянная Планка. Волны, о которых идет речь, называются волнами де Бройля.

Другой вид формулы де Бройля: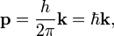 где 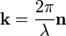-волновой вектор, модуль которого 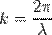- волновое число -есть число длин волн, уклад-ся на 2π единицах длины, n-един-ый вектор в напр-ии распр-я волны, 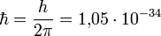Дж·с.

Длина волны де Бройля для частицы с массой m, имеющей кинетическую энергию Wk: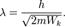

В частности, для электрона, ускоряющегося в электрическом поле с разностью потенциалов дельта φ вольт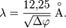

Формула де Бройля экспериментально подтверждается опытами по рассеянию электронов и других частиц на кристаллах и по прохождению частиц сквозь вещества. Признаком волнового процесса во всех таких опытах является дифракционная картина распределения электронов (или других частиц) в приемниках частиц.

Волновые свойства не проявляются у макроскопических тел. Длины волн де Бройля для таких тел настолько малы, что обнаружение волновых свойств оказывается невозможным.

Фазовая скорость волн де Бройля свободной частицы

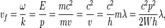
где ω = 2πν — циклическая частота, W— кинетическая энергия свободной частицы,E — полная (релятивистская) энергия частицы, p = mv — импульс частицы, m, v — её масса и скорость соответственно, λ — длина дебройлевской волны. Зависимость фазовой скорости дебройлевских волн от длины волны указывает на то, что эти волны испытывают дисперсию.

Фазовая скорость vfволны де Бройля относится к числу принципиально ненаблюдаемых величин и является чисто математическим объектом.

Волны де Бройля имеют специфическую природу, не имеющую аналогии среди волн, изучаемых в классической физике: квадрат модуля амплитуды волны де Бройля в данной точке является мерой вероятности того, что частица обнаруживается в этой точке. Дифракционные картины, которые наблюдаются в опытах, являются проявлением статистической закономерности, согласно которой частицы попадают в определенные места в приёмниках — туда, где интенсивность волны де Бройля оказывается наибольшей.