Энтропия

Из формул (2.42) и (2.47) следует, что 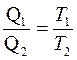и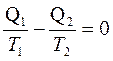

Учтем, что количество тепла Q₂, отданного холодильнику отрицательно. Тогда последнее равенство можно записать:

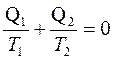. (2.48)

Отношение Q/T называется приведенной теплотой.

Приведенная теплота, переданная системе нагревателем, при бесконечно малом ее изменении, равна δQ/Т. Можно показать, что для любого обратимого кругового процесса сумма приведенных теплот равна нулю. Тогда выражение (2.48) в общем, виде может быть записано как:

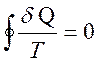(2.49)

Равенство нулю интеграла по замкнутому контуру означает, что в обратимом процессе подинтегральное выражение есть полный дифференциал некоторой функции S, зависящей только от состояния системы. Функция S называется энтропией.

Таким образом

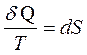(2.50)

Из формулы (2.49) следует, что для обратимых процессов изменение энтропии

ΔS = 0 . (2.51)

Можно показать, что для необратимых неравновесных процессов, происходящих в замкнутой системе, энтропия возрастает

ΔS > 0 (2.52)

Соотношения (2.51) и (2.52) объединяются в неравенство Клаузиуса:

ΔS≥0

т.е. энтропия замкнутой системы либо возрастает, либо остается постоянной.

Так как реальные процессы необратимы, то можно утверждать, что все процессы, протекающие в замкнутой системе, ведут к увеличению энтропии. Это утверждение, называемое принципом возрастания энтропии, является еще одной формулировкой второго закона термодинамики.

Физический смысл энтропии выяснил Л. Больцман, который показал, что энтропия связана с термодинамической вероятностью состояния системы. Термодинамическая вероятность w определяется как число способов, которыми может быть реализовано данное состояние системы. Согласно Больцману, связь S и w выражается формулой:

S = k lnw (2.53)

где k – постоянная Больцмана.