Магнитное поле. Французский физик А.М. Ампер экспериментально установил, что если в двух параллельных проводниках ток направлен в одну сторону
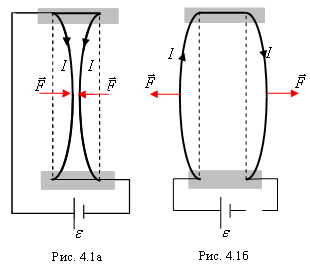 |
Французский физик А.М. Ампер экспериментально установил, что если в двух параллельных проводниках ток направлен в одну сторону, то они притягиваются друг к другу (рис. 4.1а). В случае же когда направление токов противоположное, проводники отталкиваются (рис. 4.1б). Согласно теории близкодействия силовое взаимодействие на расстоянии осуществляется посредством поля. Но взаимодействие проводников с током не может быть вызвано электрическим полем, так как токи в проводниках обусловлены движением электронов, а одноименные заряды всегда отталкиваются, тогда как из опыта Ампера следовало, что, когда токи текут в одном направлении, проводники притягиваются. Какое же поле существует вокруг движущихся электрических зарядов и обусловливает взаимодействие проводников с током?
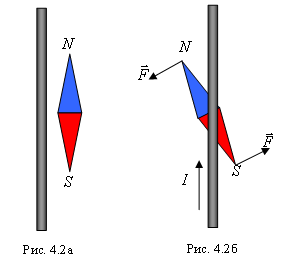 |
В 1820 г. датский физик Х.К. Эрстед проделал такой опыт. Он поместил проводник с током над установившейся в магнитном поле Земли магнитной стрелкой, расположив проводник вдоль оси магнитной стрелки (рис. 4.2а). При пропускании по проводнику тока магнитная стрелка отклонялась (рис. 4.2б) и располагалась перпендикулярно проводнику, причем направление ее отклонения зависело от направления тока в проводнике. Известно, что магнитная стрелка отклоняется под действием магнитного поля. Таким образом, опыт Эрстеда указал на наличие связи между электрическими и магнитными явлениями, которые ранее считались несвязанными друг с другом. Стало очевидно, что электрические токи могут производить магнитные эффекты, и, в свою очередь, магниты могут вызывать силы, действующие на токи.
Можно предположить, что вокруг проводника с током существует магнитное поле, и взаимодействие проводников – результат действия магнитного поля. Пока цепь в опыте Эрстеда не замкнута, магнитного поля нет, хотя в проводнике находятся электрические заряды. При замыкании цепи заряды приходят в упорядоченное движение. Вблизи провода обнаруживается магнитное поле. Можно предположить, что магнитное поле создается движущимся электрическим зарядом. Вокруг неподвижных зарядов магнитного поля нет.
Тогда можно поставить вопрос: как действует магнитное поле на электрические заряды? Поместим проводник в магнитное поле. При отсутствии тока проводник остается неподвижным. Однако при замыкании цепи проводник втягивается в межполюсное пространство магнита. При смене направления тока проводник движется в обратном направлении. Следовательно, магнитное поле не действует на электрические заряды, если они неподвижны. Но на движущиеся заряды магнитное поле действует. Таким образом, магнитное поле связано с движущимися электрическими зарядами и действует только на движущиеся заряды.
Опыт свидетельствует, что магнитное поле имеет направленный характер и должно характеризоваться векторной величиной. Можно было бы по аналогии с напряженностью электрического поля назвать ее напряженностью магнитного поля. Однако по историческим причинам основную силовую характеристику магнитного поля назвали магнитной индукцией.
Силовая характеристика электрического поля – напряженность – была определена как отношение силы, с которой поле действует на положительный заряд, к величине этого заряда:
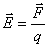 .
.
Силовую характеристику магнитного поля можно определить, рассматривая действие магнитного поля на проводник с током. Но следует учесть, что сила, с которой магнитное поле действует на пробный ток, зависит от силы тока, его направления и от длины проводника. Кроме того, как показывает опыт, если проводник с током поворачивать в постоянном магнитном поле, то величина силы будет меняться от максимального значения, когда проводники параллельны, до нуля, когда они расположены перпендикулярно друг к другу. Поэтому в качестве силовой характеристики магнитного поля можно взять отношение максимального значения силы, с которой магнитное поле действует на пробный ток, к силе тока I и длине проводника l. Эта величина и называется индукцией магнитного поля:
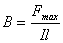 .
.
Магнитная индукция – величина векторная. Однако ее направление не совпадает с направлением силы, с которой магнитное поле действует на проводник с током. Вектор магнитной индукции направлен перпендикулярно направлению тока и направлению силы, с которой магнитное поле действует на ток. Эту связь удобно представить в виде:
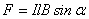 ,
,
где 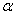 – угол между направлением тока и вектором магнитной индукции.
– угол между направлением тока и вектором магнитной индукции.
Для того чтобы направление вектора магнитной индукции 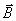 было определено однозначно, используется правило левой руки. Нужно расположить прямолинейный проводник с током в магнитном поле таким образом, чтобы сила Ампера имела максимальное значение. Раскрытую ладонь левой руки следует поместить в плоскости, проходящей через проводник с током и вектор силы Ампера. Четыре пальца руки располагаются по направлению тока в проводнике, а большой палец, отогнутый в плоскости ладони, под прямым углом к остальным четырем пальцам, – по направлению силы Ампера. Тогда вектор индукции будет входить перпендикулярно в плоскость ладони (рис. 4.3).
было определено однозначно, используется правило левой руки. Нужно расположить прямолинейный проводник с током в магнитном поле таким образом, чтобы сила Ампера имела максимальное значение. Раскрытую ладонь левой руки следует поместить в плоскости, проходящей через проводник с током и вектор силы Ампера. Четыре пальца руки располагаются по направлению тока в проводнике, а большой палец, отогнутый в плоскости ладони, под прямым углом к остальным четырем пальцам, – по направлению силы Ампера. Тогда вектор индукции будет входить перпендикулярно в плоскость ладони (рис. 4.3).
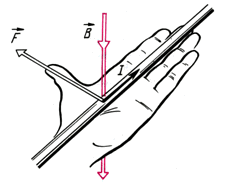 Рис. 4.3 Рис. 4.3 |
За единицу магнитной индукции принята индукция такого поля, в котором на проводник длиной 1 м при протекании в нем тока в 1 А действует максимальная сила в 1 Н. Такая единица называется тесла (Тл):
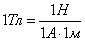 .
.
Тесла – очень крупная единица. Индукция магнитного поля Земли приблизительно равна 0.5·10-4 Тл. Большой лабораторный электромагнит может создать поле с индукцией не более 5 Тл.
Задать вектор 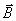 в каждой точке магнитного поля сложно. Однако, как и в случае электростатического поля, магнитное поле можно описать с помощью магнитных силовых линий. Вектор магнитной индукции в каждой точке поля направлен по касательной к магнитной силовой линии. Силовые линии магнитного поля непрерывны. В отличие от потенциального электростатического поля, где силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных, магнитное поле является соленоидальным, или вихревым: его силовые линии всегда замкнуты. Другими словами, магнитное поле не имеет источников – магнитных зарядов.
в каждой точке магнитного поля сложно. Однако, как и в случае электростатического поля, магнитное поле можно описать с помощью магнитных силовых линий. Вектор магнитной индукции в каждой точке поля направлен по касательной к магнитной силовой линии. Силовые линии магнитного поля непрерывны. В отличие от потенциального электростатического поля, где силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных, магнитное поле является соленоидальным, или вихревым: его силовые линии всегда замкнуты. Другими словами, магнитное поле не имеет источников – магнитных зарядов.
 |
Картину магнитных силовых линий можно сделать «видимой». Для этого можно использовать мелкие железные опилки, которые намагничиваются в магнитном поле и устанавливаются вдоль силовых линий. Опыт показывает, что магнитные силовые линии прямого проводника с током представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику; центры этих окружностей находятся на оси проводника.
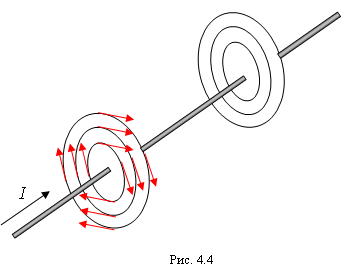
Если вместо опилок взять стрелочку компаса, то можно видеть, что она устанавливается по касательной к линиям поля. При изменении направления тока в проводнике направление стрелки меняется на противоположное. Это позволяет предложить простое правило для нахождения направления вектора 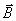 : если смотреть вдоль проводника по направлению тока, то есть по направлению движения положительных зарядов, то вектор магнитной индукции направлен по касательной к линии индукции в направлении хода часовой стрелки (рис. 4.4).
: если смотреть вдоль проводника по направлению тока, то есть по направлению движения положительных зарядов, то вектор магнитной индукции направлен по касательной к линии индукции в направлении хода часовой стрелки (рис. 4.4).
На рис. 4.5а приведена картина силовых линий кругового тока, полученная с помощью магнитных опилок, на рис. 4.5б – картина силовых линий магнитного поля длинной катушки-соленида, на рис. 4.5в – прямого постоянного магнита.
 Рис. 4.5в Рис. 4.5в |  Рис. 4.5а Рис. 4.5а |  Рис. 4.5б Рис. 4.5б |
3.2. Закон Био–Савара
Магнитное поле удовлетворяет принципу суперпозиции: если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником. Точно так же для однородного проводника с током наблюдаемая на опыте индукция 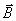 есть векторная сумма элементарных индукций D
есть векторная сумма элементарных индукций D 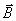 полей, создаваемых отдельными элементами проводника с током
полей, создаваемых отдельными элементами проводника с током 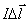 , где
, где 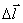 – вектор, совпадающий по направлению с направлением тока в проводнике, а по модулю равный длине проводника.
– вектор, совпадающий по направлению с направлением тока в проводнике, а по модулю равный длине проводника.
 |
На опыте невозможно осуществить отдельный участок тока, поэтому измерить можно только индукцию магнитного поля, создаваемого всеми элементами тока. Существует закон, который позволяет определить индукцию магнитного поля, созданного отдельным элементом проводника с током. Это закон Био–Савара, согласно которому
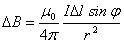 , , | (4.1) |
где j – угол между направлением на точку наблюдения, определяемым радиус-вектором 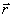 и направлением элемента тока
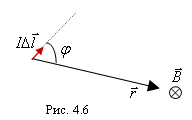
и направлением элемента тока 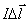 , которое совпадает с направлением тока в проводнике, r – расстояние от элемента тока до точки наблюдения, причем
, которое совпадает с направлением тока в проводнике, r – расстояние от элемента тока до точки наблюдения, причем 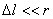 , m0 – магнитная постоянная (рис. 4.6). Магнитная постоянная вводится в системе единиц СИ при определении единицы измерения силы тока на основании закона взаимодействия токов. Вектор
, m0 – магнитная постоянная (рис. 4.6). Магнитная постоянная вводится в системе единиц СИ при определении единицы измерения силы тока на основании закона взаимодействия токов. Вектор 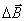 перпендикулярен плоскости, в которой лежат элемент тока
перпендикулярен плоскости, в которой лежат элемент тока 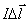 и радиус-вектор
и радиус-вектор 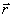 . Направление вектора
. Направление вектора 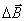 определяется направлением поступательного движения правого винта, если его головку поворачивать от вектора
определяется направлением поступательного движения правого винта, если его головку поворачивать от вектора 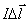 к вектору
к вектору 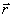 в направлении, соответствующем минимальному значению угла
в направлении, соответствующем минимальному значению угла 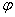 . Используя принцип суперпозиции, можно с помощью закона Био–Савара рассчитать значение результирующей индукции магнитного поля, создаваемого проводником с током любой формы. Например, для величины индукции магнитного поля бесконечного прямолинейного проводника с током получается выражение
. Используя принцип суперпозиции, можно с помощью закона Био–Савара рассчитать значение результирующей индукции магнитного поля, создаваемого проводником с током любой формы. Например, для величины индукции магнитного поля бесконечного прямолинейного проводника с током получается выражение
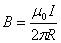 ,
,
где R – расстояние от проводника до точки, в которой рассчитывается индукция магнитного поля.
Магнитное поле движущегося заряда. Ток в проводнике представляет собой направленное движение заряженных частиц. Магнитное поле тока, согласно принципу суперпозиции, складывается из магнитных полей отдельных движущихся частиц. Магнитную индукцию поля, создаваемого движущимся зарядом q, можно определить, если воспользоваться законом Био–Савара. Силу тока можно представить как 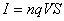 , где n – концентрация заряженных частиц, V – скорость их движения, S – площадь поперечного сечения проводника. Подставим выражение для силы тока в (4.1):
, где n – концентрация заряженных частиц, V – скорость их движения, S – площадь поперечного сечения проводника. Подставим выражение для силы тока в (4.1):
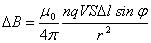 .
.
Произведение 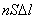 дает полное число носителей заряда N внутри элемента тока
дает полное число носителей заряда N внутри элемента тока 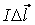 , тогда
, тогда
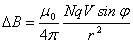 . . | (4.2) |
Поделив полученное выражение на N, получим индукцию магнитного поля, созданного зарядом q, движущимся со скоростью V:
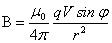 ,
,
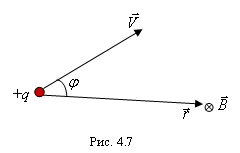 здесь r – расстояние от заряда до точки наблюдения, φ – наименьший угол между скоростью заряда и радиус-вектором, определяющим положение точки наблюдения относительно заряда, создающего поле (рис. 4.7).
здесь r – расстояние от заряда до точки наблюдения, φ – наименьший угол между скоростью заряда и радиус-вектором, определяющим положение точки наблюдения относительно заряда, создающего поле (рис. 4.7).
Магнитное поле кругового проводника. Картина силовых линий кругового проводника с током представлена на рис. 4.4. 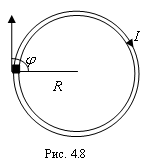 Рассчитаем магнитную индукцию в центре кругового тока. Пусть ток идет по проводу в виде окружности радиуса R по часовой стрелке. Векторы
Рассчитаем магнитную индукцию в центре кругового тока. Пусть ток идет по проводу в виде окружности радиуса R по часовой стрелке. Векторы 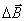 от всех элементов тока будут направлены перпендикулярно плоскости чертежа за чертеж (рис. 4.8). Поэтому, чтобы найти значение индукции магнитного поля
от всех элементов тока будут направлены перпендикулярно плоскости чертежа за чертеж (рис. 4.8). Поэтому, чтобы найти значение индукции магнитного поля 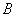 , созданного круговым витком с током, можно алгебраически сложить модули всех векторов
, созданного круговым витком с током, можно алгебраически сложить модули всех векторов 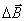 , обусловленных отдельными элементами тока. Для каждого элемента тока угол
, обусловленных отдельными элементами тока. Для каждого элемента тока угол 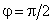 , поэтому
, поэтому
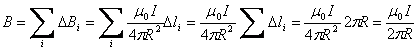 .
.
