T-S-диаграмма. Доказательство теоремы Карно

Из определения энтропии (8.41) следует

.

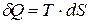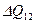Проинтегрировав это выражение, можно найти количество теплоты , полученной системой при переходе из состояния с энтропией, равной S₁, в состояние с энтропией S₂:

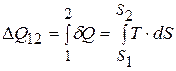. (8.51)

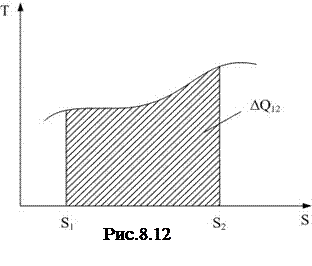
В соответствии с (8.51) количество теплоты 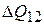можно найти как площадь под графиком функции в пределах от S₁ до S₂ (рис.8.12).

Используя T-S-диаграмму, можно доказать теорему Карно. Первая часть теоремы Карно гласит:

1) КПД цикла Карно не зависит от природы рабочего тела и определяется только температурами нагревателя и охладителя:

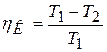. (8.38)

Доказательство:

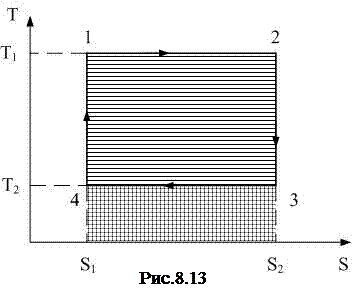
На рис.8.13 изображён цикл Карно в осях T-S. Процесс 1→2 – это изотермическое расширение при температуре T₁ нагревателя (энтропия при расширении возрастает); 3→4 – это изотермическое сжатие при температуре T₂ охладителя (энтропия уменьшается). Процесс 2→3 – это адиабатическое расширение (температура при этом понижается), 4→1 – адиабатическое сжатие (температура повышается). КПД теплового двигателя равен

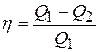, (8.37)

где Q₁ – количество теплоты, полученной рабочим телом от нагревателя, Q₂ – количество теплоты, отданной рабочим телом охладителю. Пользуясь свойством T-S-диаграммы, из графика рис.8.13 определим Q₁ – это площадь под отрезком 1-2 (горизонтальная штриховка):

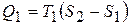. (8.52)

Аналогично, Q₂ – это площадь под отрезком 3-4 (вертикальная штриховка):

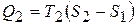. (8.53)

Тогда получим:

.

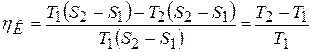Вторая часть теоремы Карно:

2) КПД любого обратимого цикла не больше КПД цикла Карно с теми же температурами нагревателя и охладителя:

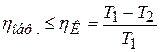. (8.54)

Доказательство:

Рассмотрим произвольный обратимый цикл abcda (рис.8.14) с температурами нагревателя и холодильника Т₁ и Т₂ соответственно. На T-S-диаграмме опишем цикл Карно 12341 как прямоугольник вокруг обратимого цикла. КПД обратимого цикла

,

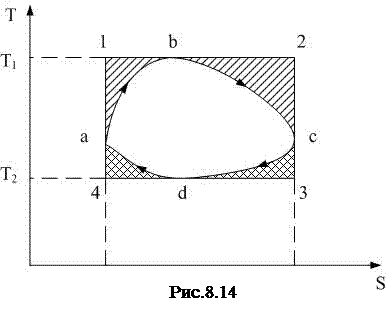
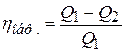где Q₁ – количество теплоты, полученной рабочим телом от нагревателя, равно площади под кривой abc и не больше площади под изотермой 1→2 цикла Карно:

.

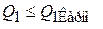Q₂ – количество теплоты, отданной рабочим телом нагревателю, равно площади под кривой adc и не меньше площади под изотермой 3→4 цикла Карно:

.

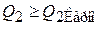Тогда получим:

.

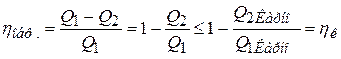Третья часть теоремы Карно:

3) КПД любого необратимого цикла меньше КПД цикла Карно с теми же температурами нагревателя и охладителя:

. (8.40)

Доказательство:

Рассмотрим необратимый цикл с температурами Т₁ и Т₂ нагревателя и холодильника соответственно. Из-за необратимости максимальная температура рабочего тела Т_1Р.Т. будет меньше Т₁, а минимальная Т_2Р.Т. – больше Т₂:

, .

Тогда

.

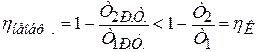Свободная энергия

Из второго начала термодинамики вытекает, что не вся внутренняя энергия нагретого тела может быть превращена в эквивалентную ей работу; иначе можно было бы создать тепловую машину с КПД, равным 100%.

Определим свободную энергию F как часть внутренней энергии, которую можно превратить в работу в изотермическом процессе:

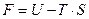. (8.55)

Свободная энергия является функцией состояния системы.

Найдём приращение свободной энергии из (8.55):

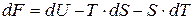. (8.56)

Из (8.41) 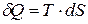, тогда

. (8.57)

По первому началу термодинамики 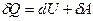, тогда из (22) получим:

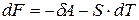. (8.58)

В изотермическом процессе dT=0, и

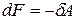, (8.59)

то есть работа совершается за счёт убыли свободной энергии. Физический смысл свободной энергии можно сформулировать так: работа, совершаемая системой в обратимом изотермическом процессе, равна убыли свободной энергии системы.

Произведение 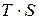в (8.55) можно назвать «связанной» энергией, так как её нельзя превратить в работу.

Энтальпия

По определению, энтальпией H называется функция состояния, равная:

. (8.60)

При постоянном давлении

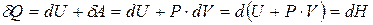. (8.61)

Отсюда можно сформулировать физический смысл энтальпии: изменение энтальпии системы при постоянном давлении равно количеству теплоты, сообщённому системе.

Поэтому энтальпию также называют теплосодержанием.