Принцип неопределенности Гейзенберга

И свет, и микрочастицы в любой момент одновременно являются и частицей и волной. Только в некоторых случаях одно из свойств выражено меньше. Например, для электромагнитной волны частотой меньше 10¹² с^–1 (это радиоволны) корпускулярные свойства практически невозможно обнаружить, а гамма-излучение (частота больше 10²⁰ с^–1) ведет себя как частица и не проявляет волновых свойств. Рентгеновское и видимое излучение занимают промежуточное положение (10¹⁵ ≤ ω ≤ 10¹⁹ с^–1), и для этих видов мы можем наблюдать как корпускулярные свойства (фотоэффект, эффект Комптона), так и волновые свойства (дифракция, интерференция). Если же говорить о волновых свойствах частиц, то тут правила еще проще: чем мельче частица, тем заметнее для нее волновые свойства, если же частицу заставить расти, то волновые свойства быстро теряются и остаются только корпускулярные. Можно даже сказать, что каждый из нас обладает волновыми свойствами, однако этот эффект настолько мал, что ни зарегистрировать его каким либо прибором, ни использовать для получения, например, дифракции не возможно. И этот факт наглядно отражен в одном из основных принципов квантовой физики – это принцип неопределенности Гейзенберга.

Для понимания ниже сказанного уточним, что понятие неопределенность здесь имеет смысл некоторого интервала ∆x, в который укладывается значение величины x. То есть, если ∆x = 0, то это значит, что мы имеем точное (или определенное) значение величины x. Итак, одна из возможных формулировок принципа неопределенности гласит:

Произведение неопределенностей координаты ∆x частицы и проекции ее импульса ∆p_x на ту же ось не может по порядку величины быть меньше постоянной планка ħ: 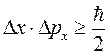(4.5)

Если сказать другими словами, то чем точнее мы можем измерить одну из указанных величин, тем больший разброс будет иметь вторая.

Рассмотрим движение частицы вдоль оси Y, на пути которой установлено препятствие с небольшим отверстием (рис. 4.4). До прохождения через отверстие частица имеет вполне определенное значение проекции импульса на ось х, так как по условию задачи известно, что перемещение частицы происходит в заданном направлении.

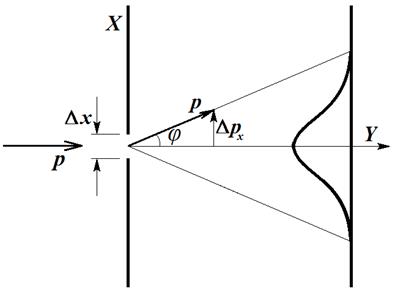
Рис. 4.4. Прохождение частицы через отверстие малой ширины

Однако при этом мы совершенно не знаем, в какой точке находится частица в каждый момент времени. Знаем, куда движется, не знаем, где находится, и наоборот! То есть для частицы квантовой природы утрачивает смысл понятие траектория.

В тот момент, когда частица проходит через отверстие, мы можем указать для нее довольно точное местоположение – ее координата попадет в интервал ∆x, равный ширине отверстия. В тот же самый момент происходит изменение импульса частицы. Его значение становится неопределенным ровно на столько, на сколько определенным стало значение координаты частицы.

То есть мы получаем некоторый разброс в направлении движения частицы после прохождения преграды, что и отражается в виде появления ненулевого ∆p_x. Как показывают эксперименты, вследствие дифракции, частица может вылететь в любом направлении в пределах угла 2φ (рассматриваем центральный дифракционный максимум, так как при дифракции на одной щели интенсивность остальных максимумов пренебрежимо мала). Вероятность движения под некоторым углом φ можно измерить, определив степень почернения в точке А на фотопластинке. Как видно из рисунка частица, прошедшая под таким углом имеет неопределенность импульса ∆p_x:

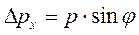(4.6)

Для первого дифракционного максимума выполняется соотношение:

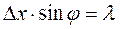
Учтем, что длина волны де Бройля может быть записана через импульс:

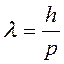
Подставляем в формулу (4.6):

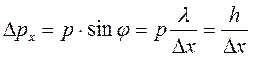(4.7)

Отсюда получаем: 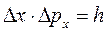(4.8)

Если учесть, что наблюдаются также еще и максимумы второго и бóльших порядков, то математически это означает, что ∆x будет больше, чем мы учли в формуле (4.8). Следовательно, произведение 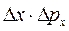будет больше: 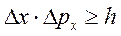(4.9)

Таким образом, мы пришли к соотношению неопределенности Гейзенберга.

Соотношение, аналогичное (4.5), можно записать для другой пары физических величин – энергии и времени:

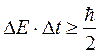(4.10)

Выполнение этого условия определяет естественную ширину спектральных линий. На схемах спектры атомов рисуют в виде тонких линий. У реальных линий есть определенная ширина – интервал энергий ∆Е, который соответствует данному энергетическому состоянию. Используя формулу (4.10), можно оценить ∆Е. Время жизни в возбужденном состоянии составляет ∆t ≈ 10^–8 с. Тогда неопределенность энергии составляет:

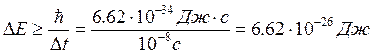
Ширину линии можно выразить через частоту:

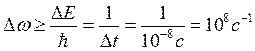
Неопределенность частоты конечно мала по сравнению с абсолютным значением частоты света (ω ~ 10¹⁵ с^–1), но она определяет «размытость» спектрального уровня и называется естественной шириной спектральной линии. Никакой высокоточный прибор, ни увеличение числа измерений не сможет позволить определить энергию спектральной линии с точностью бóльшей, чем ∆ω.

Гейзенберг и Бор показали, что ни один эксперимент не может дать результатов, противоречащих соотношениям неопределенности. Даже по отношению к массивным телам эти принципы выполняются, но ограничения, накладываемые на движение крупных тел, являются совсем ничтожными. Например, пусть маленькая капля воды диаметром 0.1 мм (m = 5·10^–10 кг) движется со скоростью V = 10 м/с. Если точность измерения ее скорости составляет 10%, то ∆p = m∆V = 5·10^–10 кг·м/с. Тогда неопределенность в определении координаты равна:

,

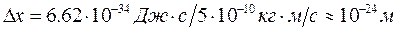что в 10²⁰ раз меньше диаметра капли. То есть координата капли в каждый момент известна с точностью 10^–24 м.

Волновая функция

Итак, микрочастицы не подчиняются законам классической механики, их поведение нельзя описать принятыми в классической физике способами. Этот факт заставил ученых создать новую теорию. Новая механика, названная квантовой, основывалась на идеях Планка, Эйнштейна, Борна и де Бройля. Основоположниками стали австриец Эрвин Шредингер (1887 – 1961), немец Вернер Карл Гейзенберг (1901 – 1976) и англичанин Поль Адриен Морис Дирак (1902 – 1984).

Одной из основных при этом стала задача математического описания поведения микрочастиц, причем такое, чтоб характеризующая их функция отражала одновременно и волновые и корпускулярные свойства.

Рассмотрим картину, образующуюся при дифракции электронов на двух щелях. В каждой точке фотопластинки степень почернения, вызванного ударами дифрагированных электронов, определяется интенсивностью волн де Бройля в направлении данной точки (рис. 4.2). Напомним, что согласно волновой теории света, число фотонов в данной точке дифракционной картины задается квадратом амплитуды световой волны, то есть ее интенсивностью. С другой стороны, число электронов в каждой точке дифракционной картины определяется вероятностью их попадания в данную точку. Чтобы учесть волновые свойства микрочастиц, де Бройль предложил рассматривать некую функцию Ψ(x,y,z,t), меняющуюся по волновому закону, т.е. как волну де Бройля (см. выше):

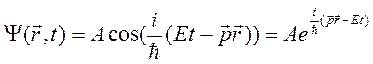(4.11)

где 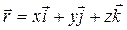– вектор, определяющий положение частицы в пространстве. Ψ(x,y,z,t) была названа волновой функцией.

Идея использовать функцию вида (4.11) возникла в связи с тем, что поведение свободной микрочастицы имело выраженную аналогию с поведением световой волны, описываемой волновыми уравнения колебаний векторов электрической и магнитной напряженностей:

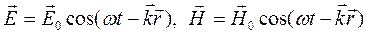(4.12)

где для учета корпускулярных свойств волновые параметры 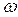и 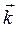заменены с учетом формул (4.1, 4.2) энергией и импульсом рассматриваемой частицы:

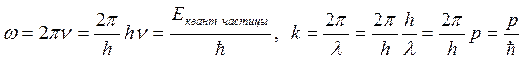(4.13)

Однако, не следует думать, что волновая функция получена простой подстановкой соответствующих параметров в выражения (4.12). Она лишь имеет аналогичную формулировку и отражает корпускулярно-волновые особенности как поведения микрочастиц, так и распространения света.

Правильную интерпретацию волновой функции дал М. Борн в 1926 г. Сама волновая функция имеет комплексное значение и не обладает физическим смыслом – то есть в природе не существует такого параметра, измерение которого дало бы значение, равное волновой функции.

Согласно Борну, физический смысл имеет квадрат модуля волновой функции, который пропорционален вероятности обнаружить частицу в момент времени t в объеме dV (dx, dy, dz) вокруг точки (x, y, z):

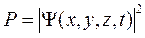(4.14)

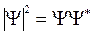(4.15)

где Ψ^* – функция, комплексно сопряженная с Ψ.

Таким образом, в квантовой механике вводится так называемая волновая функция, которая полностью описывает состояние микрочастицы и при этом отражает как ее корпускулярные, так и волновые свойства.

Вероятность обнаружить частицу в элементе объема dV равна:

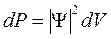(4.16)

Вероятность же нахождения частицы в конечном объеме V, согласно теореме сложения вероятностей, равна:

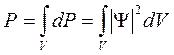(4.17)

где интегрирование проводится по координатам x, y, z. Очевидно, что сам факт существования частицы означает, что вероятность найти ее где-либо в бесконечном объеме равна 1:

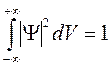(4.18)

Выражение (4.18) называется условием нормировки волновой функции.

Волновая функция Ψ (x, y, z, t) является комплексной, конечной (в противном случае вероятность обнаружения частицы может оказаться больше 1), однозначной и непрерывной. Забегая вперед, уточним, что непрерывными должны быть и частные производные , , , .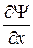

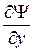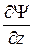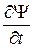Кроме того, волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями Ψ₁, Ψ₂, ...,Ψ_n, ..., то она может находиться в состоянии Ψ, описываемом линейной комбинацией этих функций:

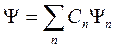(4.19)

где C_n (n = 1, 2, ...) – произвольные комплексные числа.

С помощью волновой функции можно найти средние значения физических величин, таких как средние скорость, расстояние электрона от ядра и другие. В частности средняя скорость частицы будет равна:

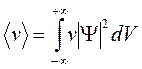(4.20)