Взаимная индукция, трансформатор
Цель работы – измерить индуктивность магнитосвязанных соленоидов. Изучить явление взаимной индукции, определить коэффициент трансформации трансформатора.
Краткое теоретическое введение
1. Магнитосвязанные соленоиды
Рассмотрим два соленоида с индуктивностями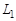 
и 
. Поставим вопрос: чему равна индуктивность системы, состоящей из этих последовательно соединенных соленоидов, если они расположены так, что магнитные поля перекрываются?
Индуктивность системы определяется потокосцеплением, т. е. общим потоком через все витки,
,
где I – сила тока в соленоидах.
Суммарный магнитный поток равен алгебраической сумме потоков, пронизывающих все витки соленоида. Все витки первого соленоида пронизываются собственным потоком 
и потоком 
, созданным вторым соленоидом. Второй соленоид пронизывается также собственным потоком 
и потоком 
, созданным первым соленоидом. Таким образом,
.
Собственные потоки всегда положительны
, 
.
«Чужие» потоки могут быть как положительными, так и отрицательными в зависимости от направления вектора магнитной индукции поля, созданного одним соленоидом в витках другого. При этом знаки магнитных потоков и всегда совпадают. Так как соленоиды соединены последовательно, то
,
где коэффициент пропорциональности L21 называется взаимной индуктивностью второго и первого контуров.
Смысл знаков определяется характером соединения и расположения соленоидов. Если магнитные поля соленоидов сонаправлены, то «чужие» потоки положительны: 
, если поля направлены навстречу друг другу, то отрицательны: 
.
Учитывая сказанное, для индуктивности системы двух соленоидов получаем
,
где знак «плюс» соответствует случаю сонаправленных полей, а «минус» – полям, направленным навстречу друг другу.
2. Взаимная индукция. Трансформатор
Явление взаимной индукции заключается в наведении ЭДС индукции в проводнике, находящемся вблизи цепи переменного тока.
Из закона электромагнитной индукции Фарадея следует, что ЭДС взаимной индукции равна
(16.1)
где 
– магнитный поток через поверхность, ограниченную вторым контуром, обусловленный магнитным полем тока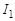 
, протекающего в первом контуре (рис. 16.1).
Рис. 16.1
Чем больше сила тока 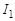в первом контуре, тем больше магнитный поток , обусловленный этим током. Поэтому, так же как и при самоиндукции, этот магнитный поток пропорционален силе тока
(16.2)
где, как говорилось выше, коэффициент пропорциональности 
называется взаимной индуктивностью (статической взаимной индуктивностью) второго и первого контуров. Этот коэффициент зависит от геометрических размеров, формы, количества витков, взаимного расположения первого и второго контуров, от магнитной проницаемости среды, в которой они находятся.
Если источник тока отключить от первого контура и подключить ко второму, создав ток 
, то для магнитного потока через площадь первого контура 
можно записать аналогичную формулу
.
Пусть контуры находятся в неферромагнитной среде, тогда, как можно показать, для них выполняется так называемая теорема взаимности, согласно которой коэффициенты взаимной индуктивности равны друг другу численно и имеют одинаковые знаки
Если же среда ферромагнитная, причем режим перемагничивания среды выходит за пределы обратимого процесса, то 
и зависят не только от вышеперечисленных параметров, но и от величины токов в контурах. В этом случае теорема взаимности не выполняется.
Заменив в законе Фарадея (16.1) магнитный поток его выражением (16.2) и полагая 
, получим
(16.3)
Если первый и второй контуры находятся в ферромагнитной среде, то можно пользоваться формулой, по виду аналогичной формуле (16.3):
(16.4)
где 
– так называемая динамическая взаимная индуктивность второго и первого контуров.
На явлении взаимной индукции основано действие трансформаторов, которые применяются для повышения или понижения напряжения переменного электрического тока.
Трансформатор (рис. 16.2) состоит из двух или нескольких соленоидальных обмоток, расположенных близко друг от друга и чаще всего закрепленных на общем ферромагнитном сердечнике. Концы пер-вичной обмотки присоединены к источнику переменного тока, а кон-
цы вторичной обмотки включены в цепь потребителя электрической энергии.
Переменное магнитное поле тока 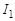, протекающего в первичной обмотке трансформатора, вызывает появление ЭДС взаимной индукции во вторичной обмотке. Магнитное поле первичной обмотки практически полностью локализовано в ферромагнитном сердечнике, играющем роль магнитной цепи. Поэтому применение в трансформаторе такого замкнутого сердечника, общего для обеих обмоток, позволяет резко увеличить магнитный поток взаимной индукции и взаимную индуктивность.
Определим статическую и динамическую взаимные индуктивности обмоток трансформатора.
|
|
Рис. 16.2
Пусть Ф – магнитный поток в сердечнике. Тогда магнитный поток через 
витков вторичной обмотки равен
Следовательно, из формул (16.2) и (16.4) получим
. (16.5)
Статическая и динамическая индуктивности первичной обмотки трансформатора в режиме холостого хода, соответствующего разомкнутому состоянию вторичной цепи 
,равны
. (16.6)
ЭДС самоиндукции в первичной обмотке можно выразить формулой
Найдем отношение абсолютных значений напряжений 
и 
на концах вторичной и первичной обмоток при холостом ходе, называемоекоэффициентом трансформации.
При разомкнутой вторичной обмотке (холостой ход) 
. В этом случае напряжение на ее концах численно равно ЭДС взаимной индукции 
(16.7)
На концах первичной обмотки напряжение , как можно показать с помощью закона Ома, равно
(16.8)
где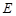 
– ЭДС источника тока; 
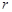– внутреннее сопротивление источника тока, подключенного к первичной обмотке трансформатора.
Сила тока в первичной обмотке согласно закону Ома для замкнутой цепи определяется формулой
где 
– ЭДС самоиндукции в первичной обмотке;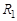 
– сопротивление первичной обмотки.
Выражая 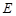и подставляя в (16.8), получаем
Как правило, для трансформаторов первый член в правой части пренебрежимо мал по сравнению со вторым. Поэтому приближенно можно считать, что
(16.9)
Зная и , используя формулы (5),(6),(7),(9), находим коэффициент трансформации
. (16.10)
Схемы измерений
| |||
| |||
|
|
Рис. 16.3 Рис. 16.4
Задание к работе
1. Измерьте индуктивность системы двух намотанных друг на друга соленоидов при совпадающем (рис. 16.3) и встречном (рис. 16.4) направлениях токов пользуясь любым из двух методов, описанных
в лабораторной работе № 15. Объясните полученные результаты.
2. Подключите звуковой генератор к соленоиду 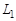, который будет играть роль первичной обмотки трансформатора, и подайте на него переменное напряжение некоторой частоты. При этом соленоид , намотанный на общий каркас с соленоидом 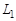, будет вторичной обмоткой.
3. Измерьте с помощью осциллографа (см. Приложение) амплитудные значения напряжения на концах первичной и разомкнутой (режим холостого хода) вторичной обмоток. Вычислите коэффициент трансформации по формуле (16.10) как отношение измеренных напряжений. Проверьте, близко ли полученное значение коэффициента трансформации к количеству витков в обмотках.
4. Проведите измерения коэффициента трансформации для трансформатора с ферромагнитным сердечником.
Контрольные вопросы
1. Как определить индуктивность системы двух близко расположенных соленоидов?
2. Почему индуктивность системы зависит от относительного направления токов в соленоидах?
3. Когда приходится пользоваться понятием динамической индуктивности?
4. Почему в трансформаторах, как правило, применяют ферромагнитные сердечники?
5. Почему ферромагнитные сердечники делают не сплошными, а собирают из изолированных друг от друга пластин?
6. Почему ферритовые сердечники трансформаторов делаются сплошными?
7. Почему обмотки трансформаторов, у которых нет ферромагнитного сердечника, наматывают одну поверх другой?
8. Что такое коэффициент трансформации?
9. Что такое режим холостого хода?
10. Как коэффициент трансформации связан с количеством витков в обмотках? Получите соответствующую формулу.
Список литературы
1. Яворский Б.М., Детлаф А.А., Милковская Л.Б. Курс физики. – М.: Высш. шк., 1964. – Т. 2.
2. Савельев И.В. Курс общей физики. – М.: Наука, 1978. – Т. 2.
Лабораторная работа № 19
ИЗУЧЕНИЕ ПЕТЛИ ГИСТЕРЕЗИСА
И ИЗМЕРЕНИЕ ПАРАМЕТРОВ ФЕРРОМАГНЕТИКОВ
Цель работы – изучить магнитные свойства и основные параметры ферромагнетиков.