Основные характеристики временной структуры сигналов

Основными характеристиками временной структуры сигналов являются: длительность Т₀, мощность P₀, энергия Э₀, спектр G(ω),амплитудно-частотный спектр |G(ω)|, фазочастотный спектр argG(ω),корреляционная функция (функция рассогласования) С(τ) , время кор­реляции τ₀, энергетический спектр S(ω), ширина спектра Δf₀, функция неопределенности ρ(τ,F), эффективная ширина сечений функции неопределенности Δτ и ΔF.

Длительность сигнала определяется как основание прямоугольни­ка, площадь которого равна площади под кривой квадрата амплитуд­ного закона модуляции (рис.1.10):

, .

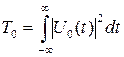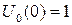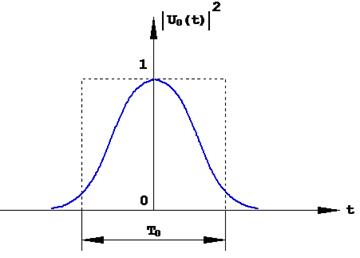
Рис.1.10. К определению длительности сигнала

Мощность сигнала определяется как усредненная во времени мгно­венная мощность сигнала

.

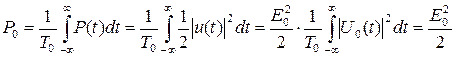Условно считаем амплитуду сигнала E₀ приведенной к нагрузке в один Ом.

Энергия сигнала определяется как проинтегрированная во времени мгновенная мощность сигнала

.

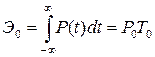Спектр сигнала характеризует распределение комплексных амплитуд (амплитуд и фаз) спектральных составляющих по частоте и опре­деляется как прямое преобразование Фурье от сигнала:

,

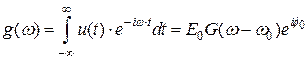где

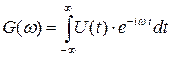
– спектр закона модуляции сигнала.

Таким образом, спектр сигнала есть смещенный по частоте на величину несущей частоты ω₀ спектр закона модуляции сигнала.

Различают амплитудно-частотный спектр сигнала (АЧС)

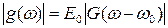
и фазо-частотный спектр сигнала (ФЧС)

.

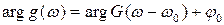Корреляционная функция (функция рассогласования) сигнала есть усредненное во времени произведение двух сигналов, рассовмещенных по времени на величину τ:

,

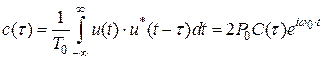где

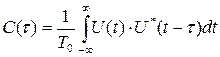
– корреляционная функция закона модуляции сигнала. Обратим внимание, что С(0)=1.

Время корреляции сигнала определяется как основание прямоу­гольника, площадь которого равна площади правого или левого "крыла" корреляционной функций (рис. 1.11)

.

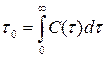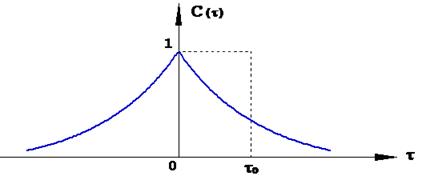
Рис.1.11. К определению времени корреляции сигнала

Энергетический спектр сигнала характеризует распределение мощности спектральных составляющих по частоте и определяется как прямое преобразование Фурье от корреляционной функции сигнала:

,

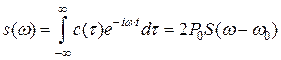где

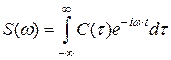
– энергетический спектр закона модуляции сигнала.

Энергетический спектр пропорционален квадрату амплитудно-частотного спектра сигнала

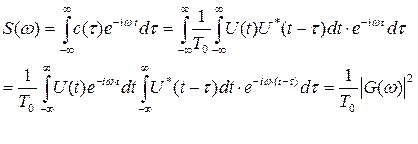
Ширина спектра закона модуляции сигнала определяется как основание прямоугольника, площадь которого равна площади под кривой энергетического спектра при одинаковой высоте и оказывается обратно пропорциональной удвоенному времени корреляции сигнала (рис. 1.12):

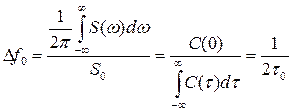
Функция неопределенности (функция Вудворда) сигнала есть квадрат модуля двумерной функции рассогласования С(τ,F) сигнала

,

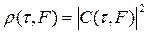которая является усредненным по времени произведением двух сигна­лов, рассовмещенных во времени на величину τ и по частоте на величину F:

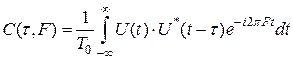
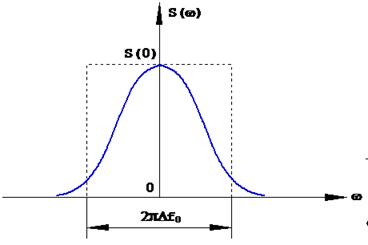
Рис.1.12. К определению ширины спектра закона модуляции.

Функция неопределенности в общем случае представляется поверхностью неопределенности (рис. 1.13).

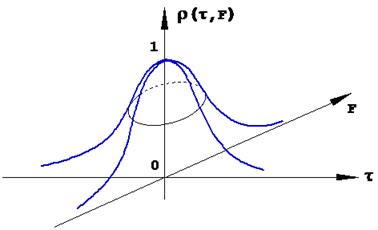
Рис.1.13. Общий вид функции неопределенности.

Обратим внимание, что двумерная функция рассогласования С(τ,F) и функция неопределенности ρ(τ,F) являются нормированными:

С(0,0)=1 , ρ(0,0)=1.

Функция неопределенности обладает рядом фундаментальных свойств.

Свойство 1. Сечение функции неопределенности плоскостью F=0 (вдоль оси τ) есть квадрат модуля функции рассогласования:

.

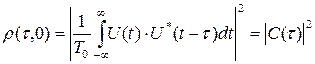Ширина этого сечения (в первом приближении) обратно пропорциональ­на ширине спектра сигнала:

.

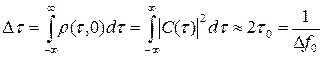Свойство 2. Сечение функции неопределенности плоскостью τ = 0 (вдоль оси F) есть нормированный энергетический спектр квадрата амплитудного закона модуляции:

.

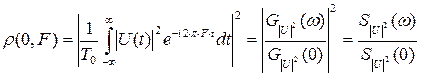Ширина этого сечения обратно пропорциональная длительности сигнала:

.

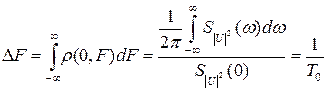Свойство 3. Функция неопределенности обладает свойством цен­тральной симметрии:

.

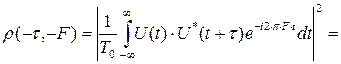
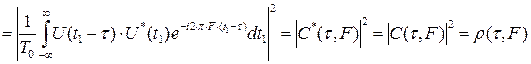Это свойство удобно иллюстрировать, используя диаграмму неопределенности. Диаграммой неопределенности называют сечение поверхности неопределенности горизонтальной плоскостью, параллельной плоскости τ, F, на таком уровне, при котором ширина этого сечения вдоль осей τ и F равна Δτ и ΔF соответственно. Диаграмма неопределенности, удовлетворяющая свойству № 3, имеет форму эллипса симметрично расположенного относительно центра (начала координат) (рис. 1.14).

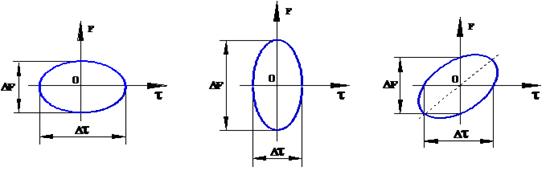
Рис.1.14. Вид диаграмм направленности, соответствующих свойству центральной симметрии.

Свойство 4. Объем тела неопределенности равен единице:

.

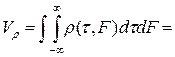
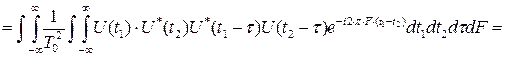
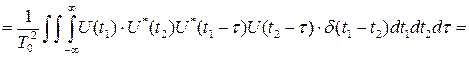
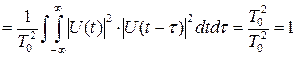Это свойство (или принцип) неопределенности означает, что никакие способы временной модуляции сигнала не могут изменить объема его тела неопределенности. Они способны лишь перераспределит этот объём над плоскостью (τ,F). Вудворд это свойство образно характеризовал так: "Тело неопределенности подобно куче песка, форму которой можно изменять, но при этом невозможно избавиться даже от одной песчинки".

Типовые одиночные сигналы

Рассмотрим несколько широко распространенных в РТС типов одиночных радиосигналов: простой прямоугольный радиоимпульс, линейно-частотно-модулированный (ЛЧМ) радиоимпульс, кодо-фазо-манипулированный (КФМ) радиоимпульс.

Простой прямоугольный радиоимпульс длительностью Т₀ показан на рис. 1.15.

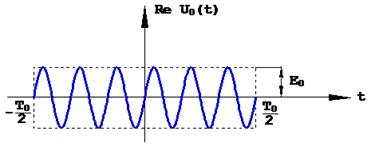
Рис.1.15. Простой прямоугольный радиоимпульс.

Его аналитическое представление

,

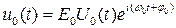где

.

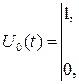
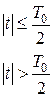Закон модуляции U₀(t) показан на рис. 1.16.

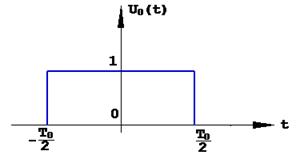
Рис.1.16. Закон модуляции простого прямоугольного радиоимпульса.

Обратим внимание, что фазовая или частотная модуляция внутри радиоимпульса отсутствует

Ψ(t) = 0.

Спектр простого прямоугольного радиоимпульса имеет форму функции sinx/x (рис. 1.17):

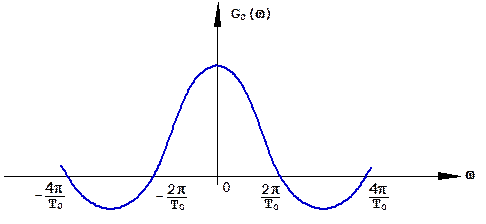
Рис.1.17. Спектр простого прямоугольного радиоимпульса.

.

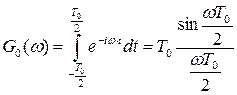Энергетический спектр имеет форму функции (sinx/x)² (рис. 1.18):

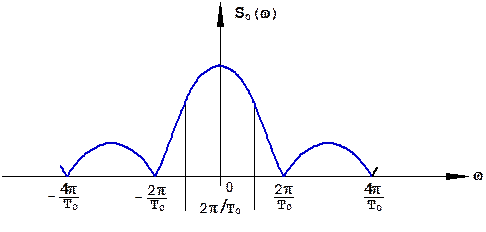
Рис.1.18. Энергетический спектр простого прямоугольного радиоимпульса.

.

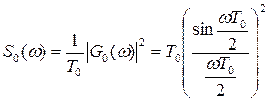Корреляционная функция простого прямоугольного радиоимпульса имеет треугольную форму (рис. 1.19):

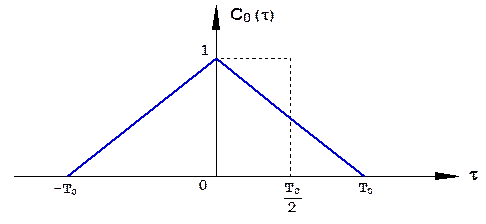
Рис.1.19. Корреляционная функция простого прямоугольного радиоимпульса

, .

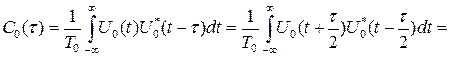
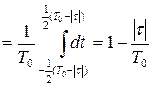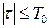Время корреляции (рис. 1.19)

,

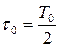ширина спектра (рис. 1.18)

.

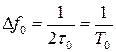Функция неопределенности простого прямоугольного радиоимпульса:

.

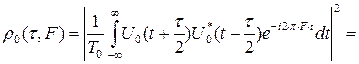
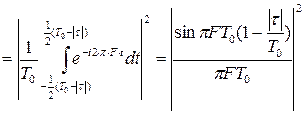Соответствующая диаграмма неопределенности простого прямоугольного радиоимпульса показана на рис. 1.20.

Рис.1.20. Диаграмма неопределенности простого прямоугольного радиоимпульса

Проявлением принципа неопределённости в случае простого прямоугольного радиоимпульса является невозможность уменьшить ширину основного лепестка функции неопределенности одновременно и вдоль оси времени τ, и вдоль оси частот F . Как следует из рис. 1.20, сужение функции неопределенности по τ за счёт уменьшения длительности радиоимпульса неизбежно приводит к расширению её вдоль оси F.

Линейно-частотно-модулированный (ЛЧМ) радиоимпульс с прямоугольной огибающей длительностью Т₀ показан на рис. 1.21.

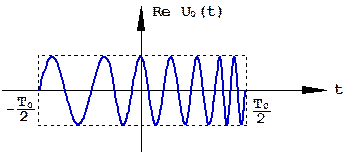
Рис.1.21. Прямоугольный ЛЧМ радиоимпульс.

Частота внутри такого радиоимпульса изменяется по линейному закону на величину частотной девиации Δf_м за время длительности сигнала Т₀ (рис. 1.22):

, .

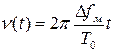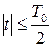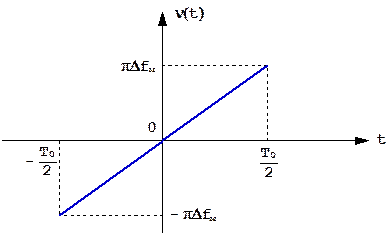
Рис.1.22. Закон частотной модуляции ЛЧМ радиоимпульса.

Линейному закону частотной модуляции соответствует квадратичный закон фазовой модуляции (рис. 1.23):

, .

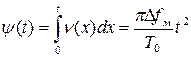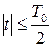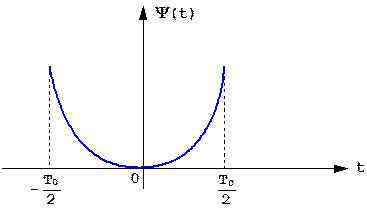
Рис.1.23. Закон фазовой модуляции ЛЧМ радиоимпульса.

Спектр прямоугольного ЛЧМ радиоимпульса

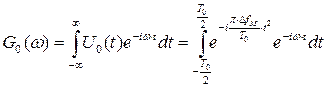
можно найти, преобразовав показатель экспоненты

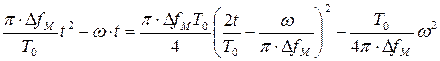
и осуществив переход к новой переменной интегрирования

.

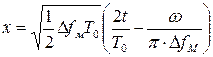Тогда

,

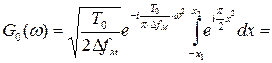
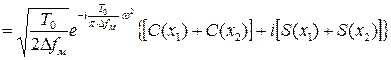где 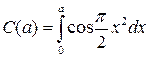– косинус-интеграл Френеля,

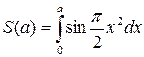– синус-интеграл Френеля,

.

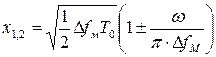Анализ соответствующего G₀(ω) амплитудно-частотного спектра

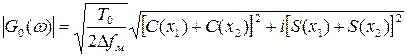
показывает, что по мере увеличения произведения Δf_мT₀ рассматриваемый спектр в полосе частот от -πΔf_м до πΔf_м становится более равномерным, а его спад на границах полосы более крутым. Это позволяет приближённо считать амплитудно-частотный, а вместе с ним и энергетический спектры закона модуляции анализируемого сигнала при больших произведениях Δf_м×T₀ прямоугольными (рис. 1.24) и с учётом того, что C(x)»S(x)»0,5 при x>>1, равными:

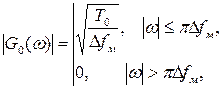
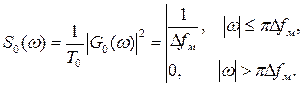
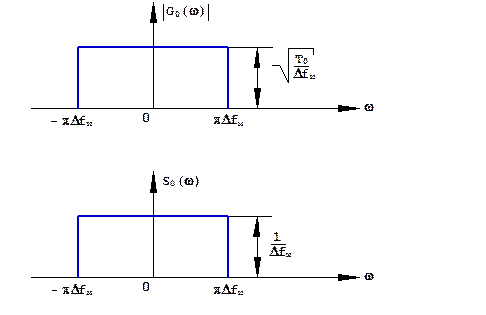
Рис.1.24. Амплитудно-частотный и энергетический спектры прямоугольного ЛЧМ радиоимпульса при Δf_м×T₀>>1

Таким образом, ширина спектра ЛЧМ радиоимпульса при Δf_м×T₀>>1 равна девиации частоты Δf₀ = Δf_м.

Для фазочастотного спектра ЛЧМ радиоимпульса

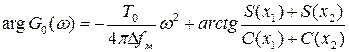
при Δf_м×T₀>>1 может быть принята параболическая аппроксимация (рис. 1.25)

,

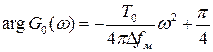поскольку его второе слагаемое даже при сравнительно небольших произведениях Δf_м×T₀ в полосе частот от -πΔf_м до πΔf_м практически постоянно и равно π/4:

.

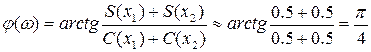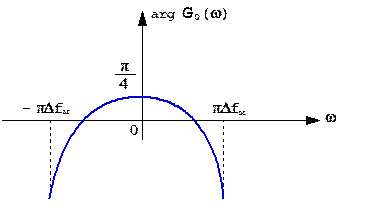
Рис.1.25. Фазо-частотный спектр прямоугольного ЛЧМ радиоимпульса при Δf_м×T₀>>1

Корреляционная функция закона модуляции прямоугольного ЛЧМ радиоимпульса, найденная как обратное преобразование Фурье от энергетического спектра S₀(ω), имеет вид (рис. 1.26):

.

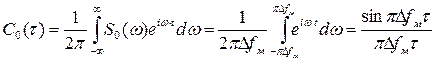Однако следует иметь в виду, что описываемая этим выражением форма корреляционной функции типа sinx/x является приближённой, справедливой при больших произведениях Δf_м×T₀ , точное выражение может быть получено непосредственно из интегрального представления корреляционной функции:

.

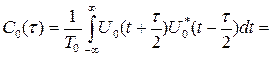
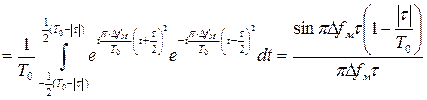Время корреляции ЛЧМ радиоимпульса значительно меньше его длительности

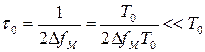, Δf_мT₀>>1.

Функция неопределенности рассматриваемого сигнала определяется выражением

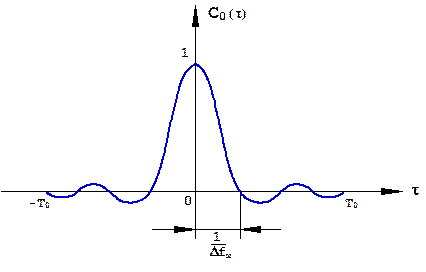
Рис.1.26. Корреляционная функция закона модуляции прямоугольного ЛЧМ радиоимпульса.

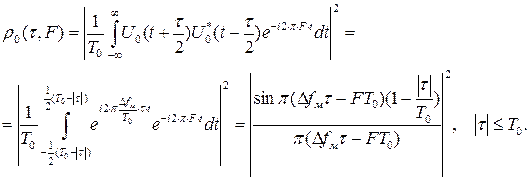
Диаграмма неопределённости изображена на рис. 1.27. Из рис. 1.27. видно, что в случае ЛЧМ радиоимпульса существует возможность одновременного сужения основного лепестка функции неопределённости и вдоль оси времени, и вдоль оси частот за счет увеличения соответственно девиации частоты и длительности радиоимпульса.

Кодофазоманипулированный (КФМ) радиоимпульс представляет собой последовательность примыкающих друг к другу простых прямоугольных радиоимпульсов (парциальных радиоимпульсов, дискретов), амплитуда, длительность и частота несущих колебаний которых одинаковы, а начальные фазы либо одинаковы, либо отличаются на постоянную величину, чаще всего равную π радиан (рис. 1.28).

Такой радиоимпульс описывается выражением

,

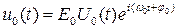где 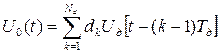– закон модуляции КФМ радиоимпульса,

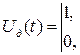
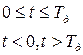– закон модуляции дискрета,

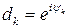– символ кода,

ψ_k – определяемая кодом начальная фаза k-го дискрета.

Рис.1.27. Диаграмма неопределенности прямоугольного ЛЧМ радиоимпульса.

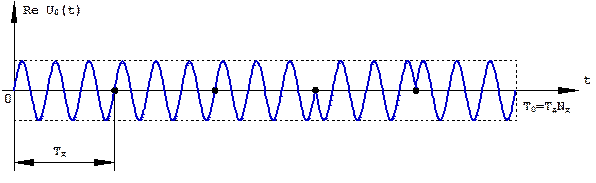
Рис.1.28. КФМ радиоимпульс.

Очевидно, при ψ_k = 0, π символы кода d_k = +1,-1. Примером кодов, используемых при внутриимпульсной кодофазовой модуляции импульсных сигналов, может служить код Баркера. Этот код существует только для N_d = 2,3,4,5,7,11,13. Последовательности символов d_k соответствующих коду Баркера, при указанных N_d приведены в табл.1.1.

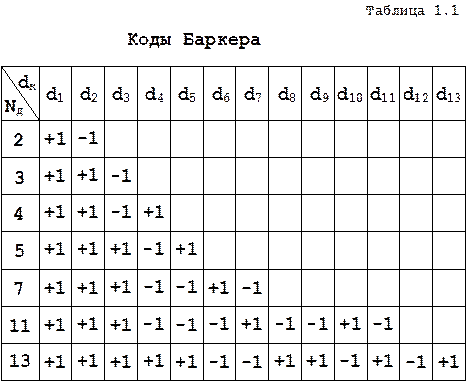
Кодирование начальных фаз дискретов непрерывных КФМ сигналов часто осуществляется в соответствии с так называемым кодом нулевой последовательности максимальной длительности (кодом М-последовательности). Этот периодический код, содержащий в периоде повторения N_d = 2ⁿ–1 символов, где n – произвольное число натурального ряда. Семиэлементные коды нулевой последовательности и Баркера совпадают. На рис. 1.29 показан закон модуляции семиэлементного кода Баркера.

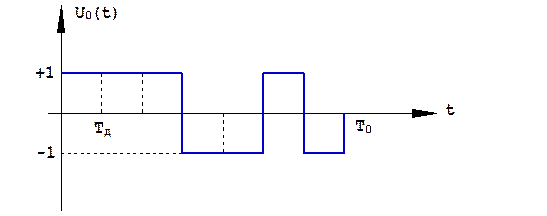
Рис. 1.29. Закон модуляции семиэлементного кода Баркера.

Корреляционная функция закона модуляции рассматриваемого сигна­ла равна

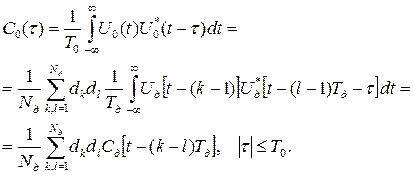
В случае N_d = 7 вид корреляционной функции закона модуляции С₀(τ) приведен на рис. 1.30. Из рисунка видно, что основной лепесток корреляционной функции КФМ радиоимпульса определяется корреляционной функцией парциального радиоимпульса.

Поэтому и энергетический спектр КФМ радиоимпульса в основном определяется энергетическим спектром парциального радиоимпульса:

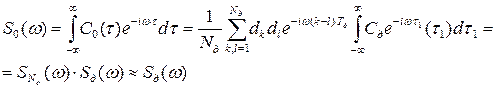
где S_d(ω) – энергетический спектр закона модуляции парциального радиоимпульса, S_Nd(ω) – энергетический спектр кода, в первом приближении равный единице.

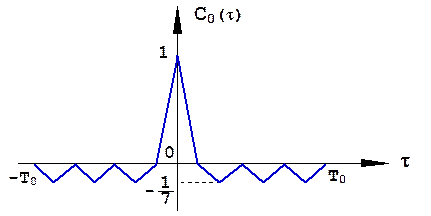
Рис.1.30. Корреляционная функция закона модуляции КФМ радиоимпульса при N_d = 7.

Время корреляции KФM радиоимпульса

,

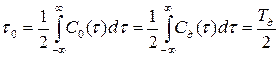а ширина его спектра

.

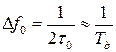Сечения функции неопределённости KФМ сигнала вдоль осей τ и F согласно её общим свойствам соответственно равны:

,

,

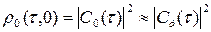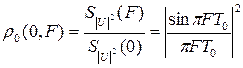а соответствующая этим сечениям диаграмма неопределённости КФМ сигнала изображена на рис. 1.31.

Видно, что в случае КФМ радиоимпульса также существует возможность сужения основного лепестка функции неопределённости одновременно и вдоль оси времени, и вдоль оси частот. Указанная возможность реализуется путем соответственного уменьшения длительности дискрета и увеличения за счет усложнения кода, длительности радиоимпульса.

Рис.1.31. Диаграмма неопределенности КФМ радиоимпульса.

Заметим, что у трёх рассмотренных одиночных сигналов (простой, ЛЧМ, КФМ) произведения ширины спектра на длительность, называемые базами сигналов, соответственно равны:

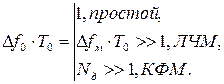
Сигналы, у которых база больше единицы, называются сложными (ЛЧМ, КФМ).