Энергетические спетры сигналов

Взаимным энергетическим спектром вещественных сигналов u(t) и v(t) называется функция: 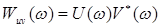, такая, что скалярное произведение этих сигналов равно:

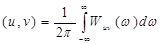
Спектральное представление энергии сигнала легко получить из обобщенной формулы Рэлея, если в ней сигналы и(t) и v(t) считать одинаковыми. Формула 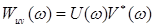, выражающая спектральную плотность энергии, приобретает вид 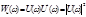Величина Wu(ω) носит название спектральной плотности энергии сигнала и(t), или, короче, его энергетического спектра.

Корреляционный анализ сигналов. Сравнение сигналов, сдвинутых по времени. Автокорреляционная функция сигнала. Связь между энергоспектром и его АКФ. Взаимнокорреляционная функция двух сигналов. Принцип определения ВКФ. Связь ВКФ с взаимной спектральной плотностью.

Корреляция, и ее частный случай для центрированных сигналов – ковариация, является методом анализа сигналов. Приведем один из вариантов использования метода. Допустим, что имеется сигнал s(t), в котором может быть (а может и не быть) некоторая последовательность x(t) конечной длины Т, временное положение которой нас интересует. Для поиска этой последовательности в скользящем по сигналу s(t) временном окне длиной Т вычисляются скалярные произведения сигналов s(t) и x(t). Тем самым мы "прикладываем" искомый сигнал x(t) к сигналу s(t), скользя по его аргументу, и по величине скалярного произведения оцениваем степень сходства сигналов в точках сравнения. Корреляционный анализ дает возможность установить в сигналах наличие определенной связи изменения значений сигналов по независимой переменной, то есть, когда большие значения одного сигнала (относительно средних значений сигнала) связаны с большими значениями другого сигнала (положительная корреляция), или, наоборот, малые значения одного сигнала связаны с большими значениями другого (отрицательная корреляция), или данные двух сигналов никак не связаны (нулевая корреляция).

АКФ.Для количественного определения степени отличия сигнала и(t) и его смещенной во времени копии u(t-τ) принято вводить автокорреляционную функцию (АКФ) сигнала u(t), равную скалярному произведению сигнала и копии:

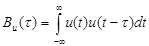(5.1)

К числу простейших свойств АКФ можно отнести ее четность:B_u(τ)=B_u(-τ). (5.2)

Важное свойство автокорреляционной функции состоит в следующем: при любом значении временного сдвига т модуль АКФ не превосходит энергии сигнала: 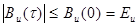(5.3) Т.е при  = 0 значение АКФ непосредственно равно энергии сигнала и является максимально возможным.

АКФ представляется симметричной кривой с центральным максимумом, который всегда положителен. При этом в зависимости от вида сигнала и(t) автокорреляционная функция может иметь как монотонно убывающий, так и колеблющийся характер.

Связь между энергоспектром и его АКФ. Спектральная плотность смещенного во времени сигнала 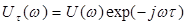, имеет вид: 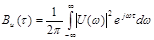. (5.4)

Квадрат модуля спектральной плотности, как известно, представляет собой энергетический спектр сигнала. Таким образом, энергетический спектр и автокорреляционная функция связаны преобразованием Фурье: 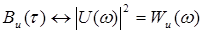(5.5)

Ясно, что имеется и обратное соотношение: 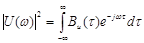. (5.6)

ВКФ.Обобщая формулу (5.1), назовем взаимокорреляционной функцией двух вещественных сигналов и(t) и v(t) скалярное произведение вида 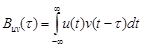(5.7)

В отличие от автокорреляционной функции одиночного сигнала,ВКФ, описывающая свойства системы двух неодинаковых сигналов, не является четной функцией аргумента τ: .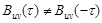

Если рассматриваемые сигналы имеют конечные энергии, то их взаимокорреляционная функция ограничена. Это утверждение следует из неравенства Коши — Буняковского: ,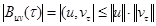

откуда 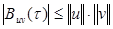, (5.10)

так как сдвиг сигнала во времени не влияет на значение его нормы.

Следует обратить внимание на то, что при τ=0 значения ВКФ вовсе не обязаны достигать максимума.

Связь ВКФ с взаимной спектральной плотностью.Выразим ВКФ двух сигналов через их спектральные характеристики. На основании обобщенной формулы Рэлея 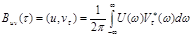и, поскольку спектр смещенного во времени сигнала 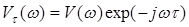, то 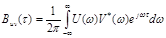Имея в виду, что величина 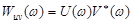есть взаимный энергетический спектр сигналов и(t) и v(t), определенный в бесконечном интервале частот -∞<ω<∞, приходим к выводу: взаимокорреляционная функция и взаимный энергетический спектр двух сигналов связаны парой преобразований Фурье.