Последовательное и параллельное соединение проводников

Электрические цепи содержат, как правило, несколько различных соединенных между собой проводников. Рассмотрим последовательное соединение проводников (рис. 3.5). Для каждого элемента цепи справедлив закон Ома. При последовательном соединении проводников сила тока в каждом из них одна и та же, а напряжение на зажимах всей схемы равно сумме напряжений на отдельных проводниках. Тогда для каждого проводника с сопротивлением падение напряжения , а падение напряжения на всей цепи . Так как , то полное сопротивление цепи при последовательном сопротивлении проводников равно сумме сопротивлений всех проводников:

.

При параллельном соединении проводников (рис. 3.6) напряжения одинаковы на всех проводниках и равны приложенному напряжению . Сила тока на входе и на выходе равна сумме сил токов, текущих через каждый из проводников, то есть

I= I_i,

где . Тогда . Отсюда

.

То есть при параллельном соединении проводников складываются величины, обратные их сопротивлениям. Сопротивление всей цепи при параллельном соединении проводников всегда меньше сопротивления каждого из них.

2.6 Последовательное и параллельное
соединение источников тока

Пусть батарею образуют n последовательно соединенных элементов. Батарея замкнута на внешнее сопротивление R (рис. 3.7). Сопротивлением соединительных проводов пренебрегаем.Запишем для всего замкнутого контура, образующего цепь, второе правило Кирхгофа. Оно имеет вид:

.

Отсюда

.

В общем случае при последовательном соединении нескольких источников с различными ЭДС сила тока определяется отношением суммы ЭДС всех источников тока к полному сопротивлению всей цепи:

,

где – внутреннее сопротивление i-го источника, R – сопротивление нагрузки.

Последовательное соединение источников эквивалентно источнику тока с большой ЭДС, однако при этом возрастает его внутреннее сопротивление. Чтобы такое соединение привело к увеличению тока в нагрузке по сравнению с током от одного источника, необходимо, чтобы . При этом .

Рассмотрим параллельное соединение в батарею n одинаковых элементов с ЭДС 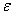и внутренним сопротивлением r (рис. 3.8). Пусть батарея замкнута на внешнее сопротивление R. Сопротивлением соединительных проводов пренебрегаем. Согласно первому правилу Кирхгофа сила тока 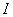в неразветвленной части цепи равна сумме сил токов во всех элементах батареи. Поэтому через каждый из элементов в отдельности протекает ток силой . Применим второе правило Кирхгофа к замкнутому участку цепи ABCDEF. Тогда получим . Отсюда . Таким образом, при параллельном соединении n одинаковых элементов в батарею ЭДС не меняется, а внутреннее сопротивление уменьшается в n раз. Легко видеть, что параллельное соединение элементов выгодно при малом внешнем сопротивлении. Действительно, если , то им можно пренебречь, и формула приближенно принимает вид , то есть сила тока возрастает в n раз по сравнению с силой тока от одного элемента.

2.7. Закон Джоуля–Ленца

Исследуя тепловое действие электрического тока, Джоуль (1818–1889) провел эксперимент, который подвел прочную основу под закон сохранения энергии. Джоуль впервые показал, что химическая энергия, которая расходуется на поддержание в проводнике тока, приблизительно равна тому количеству тепла, которое выделяется в проводнике при прохождении тока. Он установил также, что выделяющееся в проводнике тепло пропорционально квадрату силы тока. Это наблюдение согласуется как с законом Ома ( 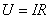), так и с определением разности потенциалов ( ). В случае постоянного тока за время t через проводник проходит заряд . Следовательно, электрическая энергия, превратившаяся в проводнике в тепло, равна:

Таким образом, если проводник, по которому течет ток, неподвижен, и в нем не совершается химических превращений, то при протекании тока в проводнике будет выделяться тепло, то есть будет увеличиваться его внутренняя энергия. Джоулем и независимо от него Ленцем было установлено, что в этом случае количество тепла, выделившееся за время , будет равно:

.

Для того чтобы найти количество тепла, выделяющееся за время в каком-то конкретном месте проводника, окружим интересующую нас точку цилиндрической поверхностью с образующей, параллельной вектору 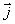. Согласно закону Джоуля–Ленца, за время в этом объеме выделится тепло:

,

где . Количество тепла, выделяющееся в единице объема за единицу времени, будет

.

Величину называют удельной тепловой мощностью.