Спонтанное и вынужденное излучение
Существование любой микросистемы (атома, молекулы, потока частиц) – это многократное изменение полной энергии этой системы в результате ее взаимодействия с другими системами. Изменение полной энергии системы принято называть переходом системы между соответствующими состояниями. Поскольку нет принципиального отличия между переходами в атомах, молекулах или других квантовых объектах, то ограничимся рассмотрением простейшей системы – атома. Начиная с теории Бора (см. раздел 3) и во всех последующих случаях мы рассматривали два вида переходов в атомах:
1) в результате поглощения энергии фотона атом переходит из основного состояния с энергией E1 в возбужденное c энергией E2.
При этом поглощение может произойти только, если энергия фотона равна разности энергий hν = (E2 – E1). Поскольку поглощательный переход – это всегда переход под действием внешнего фактора (падающий квант света не единственно возможная причина перехода), то поглощение – это всегда вынужденный переход. Вероятность такого перехода зависит от заселенности уровня E1 (т.е. от числа атомов в состоянии E1) и от плотности потока возбуждения (т.е. от числа фотонов, падающих на единичную площадку).
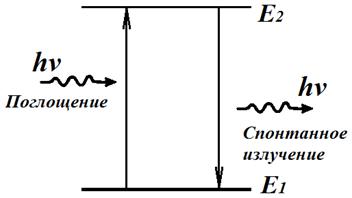
Рис. 9.1. Вынужденное поглощение и спонтанное излучение
2) если атом находится в любом состоянии выше основного, то в результате возбуждения атом самопроизвольно испустит фотон, частота которого будет равна разнице энергий уровней, между которыми произойдет переход. Такой процесс называется спонтанным излучением или флуоресценцией. Вероятность этого процесса пропорциональна только числу атомов в состоянии E2. Вероятность перехода имеет размерность числа переходов в единицу времени. Зная вероятность излучения, можно найти время жизни атома в возбужденном состоянии. В обычных условиях эта величина имеет порядок τ ~ 10–8 с. То есть спустя 10–8с после поглощения возбуждающего излучения атом сам излучит фотон и перейдет в более низкое состояние (не обязательно в основное состояние). Единственным стабильным состоянием атома является его основное состояние, т.е. самое низкое из разрешенных для него состояний (см. решение уравнения Шредингера для атома – разделы 6 и 7). В основном состоянии атом может находиться бесконечно долго, если на него не будет действовать излучение, которое спровоцирует вынужденное поглощение.
А. Эйнштейн, пытаясь объяснить наблюдающееся на опыте термодинамическое равновесие между веществом и излучением, которое оно испускает и поглощает, установил следующее: помимо поглощения и спонтанного излучения должен существовать третий, качественно иной тип взаимодействия.
Если на атом, находящийся в возбужденном состоянии E2, действует внешнее излучение с частотой, удовлетворяющей условию hν = E2 – E1, то возникает вынужденный переход в основное состояние E1 с излучением фотона той же энергии hν = E2 – E1. Этот фотон излучается дополнительно к тому фотону, под действием которого произошел переход. Возникающие при вынужденном излучении фотоны полностью тождественны фотонам, вызвавшим эти переходы. Значит эти фотоны имеют одинаковую частоту, фазу колебаний, поляризацию и направление распространения, т.е. они физически неразличимы – когерентны (см. курс «Волновой оптики», тему «Интерференция»). Испущенные фотоны двигаются в одном направлении и, встречая возбужденные атомы, стимулируют новые вынужденные переходы – происходит размножение фотонов.
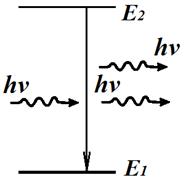
Рис. 9.2. Вынужденное излучение
Рассмотрим описанные переходы подробнее. Среди атомов, перешедших в возбужденное состояние, будут как атомы, спонтанно излучившие фотон, так и атомы, излучившие вынуждено. Причем если система термодинамически равновесна, то:
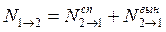 (9.1)
(9.1)
где 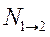 – число переходов из состояния Е1 в возбужденное состояние Е2,
– число переходов из состояния Е1 в возбужденное состояние Е2, 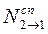 – число спонтанных переходов с уровня Е2 на уровень Е1,
– число спонтанных переходов с уровня Е2 на уровень Е1, 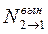 – число вынужденных переходов с уровня Е2 на уровень Е1.
– число вынужденных переходов с уровня Е2 на уровень Е1.
Т.к. для спонтанного перехода 2→1 возбуждающее излучения не требуется, то число таких переходов от свойств возбуждающего излучения не зависит: 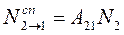 (9.2)
(9.2)
где А21 – коэффициент Эйнштейна для спонтанного перехода.
Число переходов 1→2 можно вычислить по формуле:
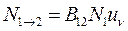 (9.3)
(9.3)
где N1 – число атомов в состоянии с энергией Е1, uν – плотность энергии падающего излучения, приходящаяся на частоту ν.
Число вынужденных переходов 2→1 записывается аналогичным образом: 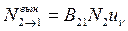 (9.4)
(9.4)
Коэффициенты в формулах (9.3) и (9.4) называются коэффициентами Эйнштейна: B12 – для поглощения, B21 для вынужденного излучения.
Согласно принципу детального равновесия, в равновесной термодинамической системе каждый микроскопический процесс сопровождается обратным ему процессом, причем вероятность обоих процессов одинакова. Основываясь на этом принципе, Эйнштейн постулировал, что вероятность W1→2 вынужденных переходов, сопровождающихся излучением, должна быть равна вероятности W2→1 вынужденных переходов, сопровождающихся поглощением света. То есть при одинаковой плотности энергии вынуждающего излучения будет выполняться:
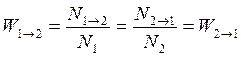 (9.5)
(9.5)
Отсюда следует, что: 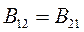 (9.6)
(9.6)
Можно показать, что 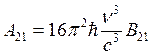 (9.7)
(9.7)
С учетом этой формулы отношение числа излучательных спонтанных переходов к числу вынужденных будет равно:
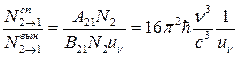 (9.8)
(9.8)
Видно, что при данной плотности возбуждающего излучения отношение в формуле (9.8) будет зависеть от ν3 вследствие чего с увеличением разности ∆Е = hν = Е2 – Е1 спонтанное излучение становится значительно более вероятным, чем вынужденное.
Рассмотрим, при каком условии вынужденные переходы будут иметь высокую вероятность. Для этого необходимо, чтобы интенсивность вынужденного излучения превышала интенсивность поглощения фотонов. Используя формулы (8.3) и (8.4) и учитывая (8.6), получим отношение числа переходов вынужденного излучения и поглощения:
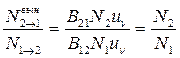 (9.9)
(9.9)
Равенство плотностей энергий вытекает из условия, что оба процесса идут одновременно, т.е. под действием одного и того же излучения.
Из формулы (9.9) видно, что интенсивность вынужденного излучения будет больше интенсивности поглощения, если заселенность уровня 2 будет больше заселенности уровня 1 (число атомов в возбужденном состоянии больше, чем число атомов в основном состоянии). Такое термодинамически неравновесное состояние называется состоянием с инверсной заселенностью, процесс получения состояния с инверсной заселенностью называется накачкой. Вещество, в котором возможно реализовать инверсную заселенность, называется активной средой.
