Теплоотдача при обтекании плоской поверхности (пластины)
ГЛАВА ТРЕТЬЯ. ТЕПЛООБМЕН В ЖИДКОСТЯХ И ГАЗАХ
ТЕПЛООТДАЧА ПРИ ОБТЕКАНИИ ПЛОСКОЙ ПОВЕРХНОСТИ (ПЛАСТИНЫ)
1. Гидродинамические условия развития процесса. При продольном течении жидкости вдоль плоской поверхности происходит образование динамического пограничного слоя, в пределах которого вследствие сил вязкого трения скорость изменяется от значения скорости невозмущеиного потока 
на внешней границе слоя до нуля на самой поверхности пластины. По мере движения потока вдоль поверхности толщина пограничного слоя постепенно возрастает; тормозящее воздействие стенки распространяется на все более далекие слои жидкости. На небольших расстояниях от передней кромки пластины пограничный слой весьма тонкий и течениежидкости в нем носит струйный ламинарный характер. Далее, на некотором расстоянии 
в пограничном слое начинают возникать вихри и течение принимает турбулентный характер. Вихри обеспечивают интенсивное перемешивание жидкости в пограничном слое, однако в непосредственной близости от поверхности они затухают и здесь сохраняется очень тонкий вязкий подслой. Описанная картина развития процесса показана на рис. 3-1.
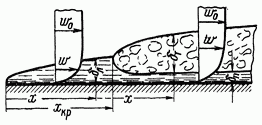
Рис. 3-1. Схема движения жидкости при обтекании пластины.
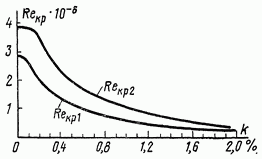
Рис. 3-2. Зависимость критического числа Re от степени турбулентности потока.
Толщина пограничного слоя 6 зависит от расстояния от передней кромки пластины, скорости потока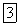 
и кинематического коэффициента вязкости v. При ламинарном пограничном слое
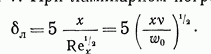
При турбулентном пограничном слое
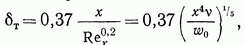
где 
— число Рейнольдса, в котором в качестве характерного оазмеоа поинято оасстояние х.
Переход к турбулентному режиму течения жидкости в пограничном слое определяется критическим значением числа Рейнольдса:
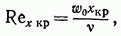
которое при продольном обтекании пластины обычно принимают равным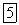 
.
Более подробный анализ показывает, что величина 
зависит от ряда факторов. Основное влияние оказывает степень начальной турбулентности набегающего потока, т. е. наличие в потоке начальных возмущений и завихрений. Степень турбулентности потока принято характеризовать отношением величины средней скорости турбулентных пульсаций 
к скорости движения потока 
, т. е. коэффициентом 
. Чем выше начальнаятурбулентность потока, тем меньше величина 
. Средняя скорость пульсаций в потоке определяется как
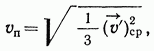
где 
— мгновенное значение вектора пульсационной скорости; 
— осреднепное во времени значение квадрата 
.
Кроме того, на величину 
может влиять шероховатость поверхности пластины, интенсивность теплообмена и т. д. Сам переход от ламинарного к турбулентному режиму течения жидкости в пограничном слое, как показывают опытные данные, происходит не в точке, а на некотором участке, в связи с чем иногда вводят два значения: 
, где 
— критическое число Рейнольдса, отвечающее переходу от ламинарного к переходному режиму течения, когда в пограничном слое возникают первые вихри и пульсации; 
— критическое число Рейнольдса для перехода к развитому турбулентному режиму течения. На рис. 3-2 приведены зависимости 
от степени начальной турбулентности набегающего потока.
Впервые теоретический расчет распределения скоростей в ламинарном пограничном слое выполнил Г. Блазиус в 1908 г. Он установил, что отношение скоростей 
зависит только от одной переменной 
, т. е. профиль скорости в пограничном слое имеет вид:
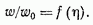
График этого профиля показан на рис. 3-3. Хотя строго теоретически 
стремится к значению 
лишь асимптотически, из рис. 3-3 видно, что уже при значении 
различие между w и 
практически исчезает (точнее, при 
). Это значение 
определяет расстояние 
, принимаемое обычно за толщинуламинарного пограничного слоя; отсюда следует формула (3-1).
Поток, обтекающий пластину, оказывает на нес определенное динамическое воздействие. Последнее проявляется в форме силы, приложенной к поверхности пластины и направленной по касательной к ней в сторону движения жидкости.
Такая касательная сила, отнесенная к единице поверхности пластины, называется касательным напряжением тления и определяется согласно закону вязкого трения Ньютона как
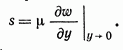
Производная 
с учетом зависимости (3-3) может быть записана
так как из рис. 3-3 видно, что
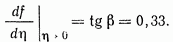
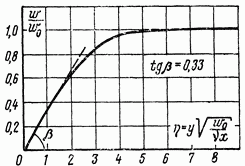
Рис. 3-3. Распределение скоростей при ламинарном режиме течения в пограничном слое.
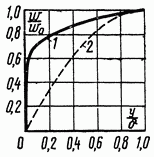
Рис. 3-4. Распределение скоростей в пограничном слое в относительных координатах. 1 — турбулентный режим течения; 2 — ламинарный режим течения.
6. Граничные условия в свою очередь бывают трех родов:
1) первого рода, задается распределение температуры на поверхности тела в функции времени;
2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;
3) третьего рода, задаются температура окружающей среды tж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:
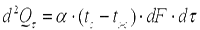 , | (9.13) |
где tc — температура поверхности тела; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2·К). Коэффициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,
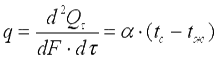 . | (9.14) |
Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности:
 . |
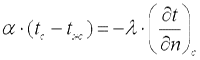Переписав последнее уравнение в виде:
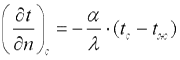 , | (9.15) |
получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.
граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:
1) первого рода, задается распределение температуры на поверхности тела в функции времени;
2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;
3) третьего рода, задаются температура окружающей среды tж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:
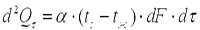 , | (9.13) |
где tc — температура поверхности тела; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2·К). Коэффициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,
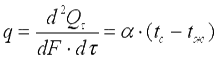| . | (9.14) |
Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности:
 . |
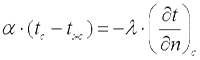Переписав последнее уравнение в виде:
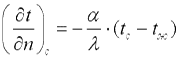 , | (9.15) |
получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.
7. Коэффициент теплопроводности. Теплопрово́дность — способность материальных тел к переносу энергии (теплообмену) от более нагретых частей тела к менее нагретым телам, осуществляемому хаотически движущимися частицами тела (атомами, молекулами, электронами и т. п.). Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества.
Теплопроводностью называется также количественная характеристика способности тела проводить тепло. В сравнении тепловых цепей с электрическими это аналогпроводимости.
Количественно способность вещества проводить тепло характеризуется коэффициентом теплопроводности. Эта характеристика равна количеству теплоты, проходящему через однородный образец материала единичной длины и единичной площади за единицу времени при единичной разнице температур (1 К). В системе СИ единицей измерения коэффициента теплопроводности является Вт/(м·K).
8. Первое начало термодинамики —один из трёх основных законов термодинамики, представляет собой закон сохранения энергии длятермодинамических систем.
Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил
Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты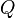 
, сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества 
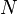при химическом потенциале 
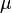, и работы 
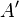[3], совершённой над системой внешними силами иполями, за вычетом работы 
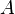, совершённой самой системой против внешних сил
.; 
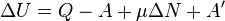