Обчислення площ плоских фігур
Застосування визначеного інтеграла до розв’язування задач з геометрії та фізики.
Обчислення площ плоских фігур.
Використовуючи поняття визначеного інтеграла, можна обчислювати площі плоских фігур. Як відомо, визначений інтеграл від невід’ємної неперервної функції є площа відповідної криволінійної трапеції. У цьому полягає геометричний зміст визначеного інтеграла, на цьому ґрунтується його застосування для обчислення площ плоских фігур.

Розглянемо криволінійну трапецію  , обмежену графіком невід’ємної, неперервної функції
, обмежену графіком невід’ємної, неперервної функції  ,
, 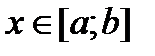 , відрізком
, відрізком 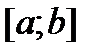 осі Ох, відрізками прямих х=а і
осі Ох, відрізками прямих х=а і  . У цьому разі площа криволінійної трапеції, як відомо, обчислюється за формулою
. У цьому разі площа криволінійної трапеції, як відомо, обчислюється за формулою
 (1)
(1)
 Приклад 1. Обчислити площу плоскої фігури, обмеженої лініями
Приклад 1. Обчислити площу плоскої фігури, обмеженої лініями  і відрізком
і відрізком  осі Ох.
осі Ох.
Розв’язання. Ця плоска фігура являє собою криволінійну трапецію, тому її площу обчислюють за формулою (1):

 Нехай тепер функція
Нехай тепер функція  ,
, 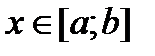 , - недодатна неперервна функція. У цьому разі графік цієї функції лежить під віссю Ох і
, - недодатна неперервна функція. У цьому разі графік цієї функції лежить під віссю Ох і
 .
.
Розглянувши допоміжну функцію  ,
, 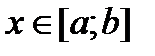 , дістанемо, що площа криволінійної трапеції
, дістанемо, що площа криволінійної трапеції  , обмеженої графіком функції
, обмеженої графіком функції  , відрізком
, відрізком 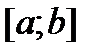 осі Ох, відрізками прямих
осі Ох, відрізками прямих  і
і  , обчислюється за формулою (1), тобто
, обчислюється за формулою (1), тобто
 (2)
(2)
Розглянемо тепер криволінійну трапецію  обмежену графіком функції
обмежену графіком функції  , відрізком
, відрізком 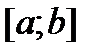 осі Ох, відрізками прямих
осі Ох, відрізками прямих  і
і  . Оскільки графік функції
. Оскільки графік функції  симетричний графіку функції
симетричний графіку функції  відносно осі Ох, то криволінійні трапеції
відносно осі Ох, то криволінійні трапеції  і
і  рівні. Як відомо, рівні фігури мають рівні площі, тому площу криволінійної трапеції
рівні. Як відомо, рівні фігури мають рівні площі, тому площу криволінійної трапеції  також обчислюватимемо за формулою (2).
також обчислюватимемо за формулою (2).
 Приклад 2. Обчислити площу фігури, обмеженої лініями
Приклад 2. Обчислити площу фігури, обмеженої лініями  ,
,  і віссю Ох.
і віссю Ох.
Розв’язання. Графік функції  ,
,  лежить під віссю Ох, тому для обчислення площі даної плоскої фігури застосовуємо формулу (2):
лежить під віссю Ох, тому для обчислення площі даної плоскої фігури застосовуємо формулу (2):
 .
.
Нехай тепер  ,
, 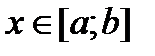 , - неперервна на відрізку
, - неперервна на відрізку 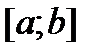 функція, графік якої перетинає відрізок
функція, графік якої перетинає відрізок 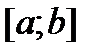 осі Ох в скінченному числі точок. З формул (1) і (2) випливає, що площу плоскої фігури, обмеженої графіком функції
осі Ох в скінченному числі точок. З формул (1) і (2) випливає, що площу плоскої фігури, обмеженої графіком функції  , відрізком
, відрізком 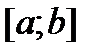 осі Ох, відрізками прямих
осі Ох, відрізками прямих  і
і  , обчислюють за формулою
, обчислюють за формулою
 . (3)
. (3)
Приклад 3. Обчислити площу плоскої фігури, обмеженої відрізком  осі Ох, графіком функції
осі Ох, графіком функції  , відрізками прямих
, відрізками прямих  і
і 

 Розв’язання. Розв’язавши рівняння
Розв’язання. Розв’язавши рівняння  , дістанемо, що графік функції
, дістанемо, що графік функції  на відрізку
на відрізку  перетинає вісь Ох у точках
перетинає вісь Ох у точках 
 . Отже, за формулою (3)
. Отже, за формулою (3) 
 Розглянемо тепер фігуру
Розглянемо тепер фігуру  , обмежену відрізками прямих
, обмежену відрізками прямих  і
і  і графіками невід’ємних неперервних функцій
і графіками невід’ємних неперервних функцій  ,
, 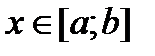 , і
, і  ,
, 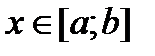 . Оскільки фігуру
. Оскільки фігуру  можна розглядати як різницю криволінійних трапецій
можна розглядати як різницю криволінійних трапецій  і
і  , то з урахуванням формули (1) дістанемо таку формулу для обчислення площі фігури
, то з урахуванням формули (1) дістанемо таку формулу для обчислення площі фігури  :
: 
(4)
 Приклад 4. Обчислити площу фігури, обмеженої лініями
Приклад 4. Обчислити площу фігури, обмеженої лініями  і
і 
Розв’язання. Розв’язавши рівняння  , знайдемо абсциси точок перетину графіків функцій
, знайдемо абсциси точок перетину графіків функцій  і
і  :
:  і
і  . Використовуючи формулу (4), обчислимо площу фігури:
. Використовуючи формулу (4), обчислимо площу фігури:

Якщо треба обчислити площу складнішої плоскої фігури, то шукану площу намагаються виразити у вигляді алгебраїчної суми площ деяких криволінійних трапецій. Так, наприклад, площу фігури, зображеної на рисунку обчислюють за формулою
 .
.
 Нехай криві АВ, ВС і АС – відповідно графіки таких функцій:
Нехай криві АВ, ВС і АС – відповідно графіки таких функцій:  ,
, 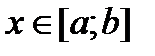 ,
, 
 , і
, і  ,
,  . Тоді
. Тоді
 . (5)
. (5)

Приклад 5. Обчислити площу плоскої фігури, обмеженої лініями  ,
,  ,
,  ,
,  , і
, і 

Розв’язання. Для знаходження площі скористаємося формулою (5):
 .
.
