Многолучевая интерференция
Интерферометр Фабри-Перо
Интерферометр Фабри-Перо, пожалуй, самый простой и вместе с тем весьма эффективный прибор, относящийся к многолучевым интерферометрам.
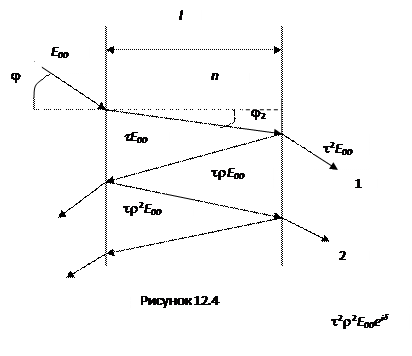
Исследуем интерференцию многих световых пучков, возникающую при прохождении плоской монохроматической волны через плоскопараллельную диэлектрическую пластинку, толщина которой l и показатель преломления n. Показатель преломления среды вне пластинки обозначим n´ (рисунок 12.4).
В большинстве ситуаций можно считать, что исследуемая диэлектрическая пластинка окружена воздухом и n´ = 1. При расчете суммарной амплитуды прошедшей волны Е20 учтем изменение амплитуды и разность фаз между двумя соседними пучками.
 |
На границе двух диэлектриков (пластинка и окружающая ее среда) амплитуда электромагнитной волны изменится. Обозначим амплитудные коэффициенты отражения и пропускания через r и t соответственно. Энергетические коэффициенты связаны с ними соотношениями R = r2 и Т = t2. В отсутствие поглощения
R + T = 1.
В данной ситуации необходимо учесть интерференцию многих световых волн постепенно уменьшающейся амплитуды, образующихся при многократных отражениях от поверхностей диэлектрической пластинки.
При каждом прохождении через границу двух диэлектриков амплитуда волны изменяется в t раз, а при каждом отражении от такой границы она изменяется в r раз. Следовательно, амплитуды вышедших из пластинки волн равны Е00t2, Е00t2r2 и т.д.
Разность фаз между двумя соседними интерферирующими пучками составляет
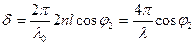 , (12.2)
, (12.2)
где l − длина волны в диэлектрической пластинке.
Учтем эту разность фаз введением соответствующего множителя 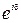 в выражение для амплитуды напряженности электрического поля. Тогда суммарная амплитуда прошедшей волны
в выражение для амплитуды напряженности электрического поля. Тогда суммарная амплитуда прошедшей волны
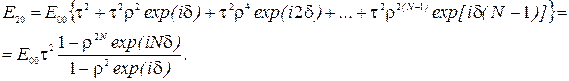 (12.3)
(12.3)
По определению, r < 1. Если число N интерферирующих пучков достаточно велико, то 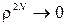 и в пределе получается
и в пределе получается
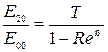 . (12.4)
. (12.4)
При вычислении отношения интенсивности света, прошедшего через диэлектрическую пластинку, к интенсивности падающего света получим:
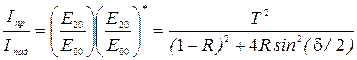 . (12.5)
. (12.5)
Это соотношение называют формулой Эйри. Исследуем ее.
Интерферирующие пучки усилят друг друга, если разность хода между ними равна целому числу длин волн, то есть справедливо условие
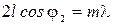 , (12.6)
, (12.6)
где т = 0, 1, 2, … .
Минимальная интенсивность будет наблюдаться при т =1/2, 3/2, …. Свяжем порядок интерференции т и введенную разность фаз между напряженностью поля в соседних пучках соотношением
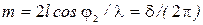 , или
, или 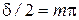 . (12.7)
. (12.7)
Интенсивность максимальна, если 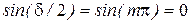 , где т – целое число. Интенсивность минимальна при
, где т – целое число. Интенсивность минимальна при 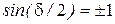 , что получает также, анализируя формулу Эйри.
, что получает также, анализируя формулу Эйри.
Анализируя формулу Эйри можно сделать следующие выводы:
· график зависимости изменения Iпр /Iпад от d имеет вид системы максимумов, форма которых при достаточно больших R существенно отличается от хорошо известной кривой вида 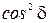 , описывающей освещенность экрана, обусловленную интерференцией двух электромагнитных волн;
, описывающей освещенность экрана, обусловленную интерференцией двух электромагнитных волн;
· чем выше коэффициент отражения R, тем острее максимумы, разделенные широкими минимумами. Такое пространственное распределение потока энергии с концентрацией его в некоторых преимущественных направлениях всегда возникает при интерференции многих пучков и четко выявляется, например, при дифракции плоской волны на правильной структуре из N щелей.
При наличии поглощения (Iпр/Iпад)мах=Т2/(А+Т)2, где А – энергетический коэффициент поглощения. При R приблизительно равном 0,9 и Т ~0,03 эта величина составляет около 9 %. Следовательно, такой интерферометр пропускает менее 10 % светового потока, который прошел бы через эквивалентный интерферометр с прозрачными (не поглощающими) слоями. Поэтому интерферометры с металлическим отражающим слоем обычно используют при исследовании ярких источников.
Анализируя формулу Эйри, можно показать, что наибольший порядок интерференции, который можно получить в интерферометре Фабри-Перо, определяется формулой 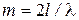 (при l = 5 см и l = 500 нм получаем т = 200000).
(при l = 5 см и l = 500 нм получаем т = 200000).
Можно показать, что угол между соседними максимумами
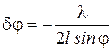 . (12.8)
. (12.8)
Отсюда следует, что чем больше l, тем уже интерференционные полосы, и выгодно работать на высоких порядках интерференции, используя толстые интерферометры. Однако это не всегда возможно. При ширине исследуемой структуры 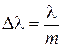 максимумы т и т+1 совпадут. Ширина исследуемой структуры и допустимое расстояние между пластинами интерферометра связаны формулой
максимумы т и т+1 совпадут. Ширина исследуемой структуры и допустимое расстояние между пластинами интерферометра связаны формулой 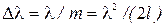 . Данное значение
. Данное значение 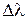 называют областью свободной дисперсии. При l = 0,5 см и l = 500 нм
называют областью свободной дисперсии. При l = 0,5 см и l = 500 нм 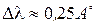 . Это значит, что интерферометр Фабри−Перо следует использовать только для исследования контуров спектральных линий, выделенных каким-либо более грубым спектральным прибором. Достаточно просто можно наблюдать интерференционную картину от интерферометра Фабри−Перо, используя в качестве источника лазер. Сферический интерферометр Фабри−Перо, предложенный П. Конном, послужил прототипом при создании конфокального лазерного резонатора.
. Это значит, что интерферометр Фабри−Перо следует использовать только для исследования контуров спектральных линий, выделенных каким-либо более грубым спектральным прибором. Достаточно просто можно наблюдать интерференционную картину от интерферометра Фабри−Перо, используя в качестве источника лазер. Сферический интерферометр Фабри−Перо, предложенный П. Конном, послужил прототипом при создании конфокального лазерного резонатора.
Известны также интерференционные светофильтры, предназначенные для выделения узкой (10 – 20 нм) спектральной области.
