Формулы для расчета газовых смесей

САМАРСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ТЕПЛОВЫХ И ГИДРАВЛИЧЕСКИХ ПРОЦЕССОВ В ТЕХНИКЕ

Методические указания к курсовой работе

по дисциплине «Математическое моделирование энергетических процессов и систем»

Курсовая работа выполняется в соответствии с выданным заданием и включает в себя расчетную и графические части.

Расчетная часть состоит из трех разделов:

1. Математическое моделирование процессов теплообмена в газовоздушном подогревателе.

2. Математическое моделирование процессов теплообмена в двигателях внутреннего сгорания.

3. Математическое моделирование тепловых и гидравлических процессов в теплообменных аппаратах.

Графическая часть работы содержит изображение цикла двигателя внутреннего сгорания (ДВС) в р-v и T-s диаграммах, изображение водо-водяного подогревателя и графика изменения температур теплоносителей по длине подогревателя.

Характерные точки циклов наносятся в соответствии с результатами расчетов в выбранном масштабе.

Математическое моделирование процессов теплообмена в газовоздушном подогревателе

Для выполнения первого раздела задания необходимо изучить следующие вопросы: параметры состояния рабочего тела, газовые смеси, теплоемкость газов.

Под газовыми смесями понимают механическую смесь нескольких газов, химически между собой не взаимодействующих. Состав газовой смеси определяется количеством каждого из газов, входящих в смесь, и может быть задан массовыми m_i или объемными r_i долями:

m_i = M_i / M; r_i = V_i / V, (1.1)

где M_i – масса i-го компонента, V_i – объем i-го компонента, а M и V – масса и объем всей смеси соответственно.

Очевидно, что

М₁ + М₂ +…+М_n = M; m₁ + m₂ +…+m_n = 1, (1.2)

а также

V₁ + V₂ +…+ V_n = V; r₁ + r₂ +…+r_n = 1. (1.3)

Для удобства решения практических задач со смесями газов введено понятие о кажущейся молекулярной массе смеси газов, которая представляет собой среднюю массу из действительных молекулярных масс отдельных компонентов смеси.

Уравнение состояния смеси газов имеет вид:

p·V = M·R_см·Т. (1.4)

На смеси газов распространяется понятие универсальной газовой постоянной

m_см·R = 8314 Дж/(кмоль×К). (1.5)

Связь между давлением газовой смеси р и парциальным давлением отдельных компонентов р_i, входящих в смесь, устанавливается законом Дальтона:

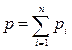. (1.6)

Если заданы состав газовой смеси, а также характеристики составляющих смесь газов, то можно рассчитать необходимые характеристики смеси по приводимым в таблице 1 формулам.

Таблица 1

Формулы для расчета газовых смесей

Задание состава смеси	Перевод из одного состава в другой	Удельный объем и плотность смеси	Кажущаяся молекуляр-ная масса смеси	Газовая постоян-ная смеси	Парциаль-ное давление
Мас-совыми долями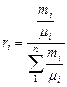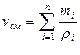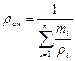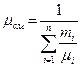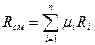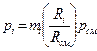
Объем-ными долями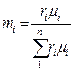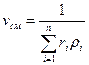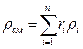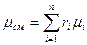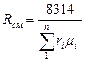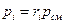

В таблице 1: m_i – молекулярная масса i-го компонента; 8314 Дж/(кмоль×К) – значение универсальной газовой постоянной; R_i – газовая постоянная i-го компонента.

Для вычисления количества теплоты полученного или отданного газом в процессе его энергетического взаимодействия с окружающей средой введено понятие теплоемкости. Под удельной теплоемкостью понимают количество теплоты, которое необходимо сообщить телу, чтобы повысить температуру какой-либо его количественной единицы на 1 ⁰С (К). В зависимости от выбранной количественной единицы различают теплоемкости:

мольную mс, кДж/(кмоль×К);

массовую с, кДж/(кг×К);

объемную с^/, кДж/(м^3×К). (1.7)

Эти теплоемкости связаны между собой следующими соотношениями:

с = mс/m ; с^/ = mс/22,4 ; с^/ = с×r_н , (1.8)

где r_н – плотность газа при нормальных условиях.

1 м³ газа имеет различную массу в зависимости от давления и температуры. В связи с этим объемную теплоемкость всегда относят к массе газа, заключенной в 1 м³ при нормальных условиях (ρ_н = 101325 Па, Т_н = 273 К). При этом объем 1 кмоля различных газов равен 22,4 м³/кмоль, а универсальная газовая постоянная - mR = 8314 Дж/(кмоль×К). В зависимости от способа подвода тепла к газу (р = const или V = const) различают изобарную с_р и изохорную с_v теплоемкости. Отношение этих величин носит название показателя адиабаты

k = mc_p/mc_v = c_p/c_v. (1.9)

Теплоемкости с_р и с_v связаны также соотношением Майера

mс_p - mc_v = mR = 8,314, кДж/(кмоль×К). (1.10)

Теплоемкость газов меняется с изменением температуры, причем эта зависимость имеет криволинейный характер. Значения истинных и средних теплоемкостей в интервале от 0⁰ до t берутся непосредственно из таблиц, причем в необходимых случаях производится интерполяция. Количество теплоты, которое необходимо затратить в процессе нагревания 1 кг газа в интервале температур от t₁ до t₂:

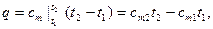(1.11)

где: c_m1 и c_m2 – соответственно средние теплоемкости в пределах 0⁰ – t₁ и 0⁰ – t₂ .

Если в процессе участвуют М (кг) или V_н (м³) газа, то:

Q_V = M(c_vm2 t₂ – c_vm1t₁) = V_н(c^/_vm2 t₂ – c^/_vm1 t₁) , кДж; (1.12)

Q_P = M(c_pm2 t₂ – c_pm1 t₁) = V_н(c^/_pm2 t₂ – c^/_pm1 t₁) , кДж. (1.13)

Теплоемкость газовой смеси следует определять по формулам:

массовая - ;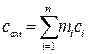

объемная - ;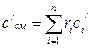

мольная - 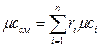. (1.14)