Потенціал. Різниця потенціалів

Потенціальна енергія взаємодії двох точкових зарядів, що знаходяться на відстані 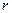, при умові, що 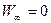, дорівнює:

.

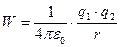Потенціал – енергетична характеристика електричного поля

,

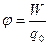де 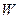– потенціальна енергія пробного заряду 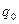, розміщеного в даній точці поля.

Робота, яку виконують сили поля по переміщенню заряду 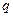із точки 1, потенціал в якій 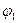, в точку 2, потенціал якої 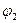, дорівнює:

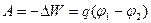, або .

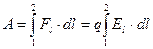В останньому виразі 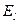– проекція вектора напруженості 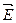на напрямок 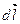, при цьому інтегрування проводимо вздовж довільної лінії, що з’єднує точки 1 та 2.

Різниця потенціалів і напруженість електричного поля пов’язані співвідношеннями:

, ,

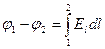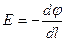де похідна 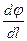береться вздовж силової лінії.

Для однорідного поля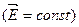

.

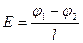Тут 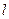– відстань між двома точками вздовж силової лінії.

Потенціал поля, яке створює точковий заряд 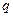на відстані 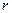від нього:

.

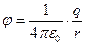Потенціал поля сферичної поверхні радіуса 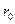, по якій рівномірно розподілений заряд 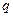, для точок, що лежать на поверхні сфери або всередині неї, рівний:

,

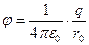а для точок, що лежать поза сферою на відстані 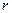від її центра,

.

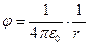Електроємність. Енергія поля

Вектор поляризації 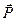вимірюється сумарним електричним моментом всіх молекулярних диполів в одиниці об'єму діелектрика. Для ізотропного діелектрика вектор 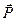пропорційний напруженості поля 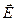всередині речовини:

,

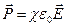де 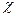- діелектрична сприйнятливість діелектрика.

Поверхнева густина 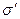зв'язаних зарядів дорівнює проекції вектора 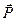на зовнішню нормаль до поверхні діелектрика:

.

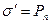Для ізотропного діелектрика вектори електричної індукції 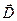і напруженості поля 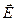зв'язані формулою:

,

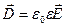де 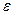– діелектрична проникність середовища, що дорівнює:

.

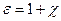Електроємність (ємність) конденсатора вимірюється відношенням його заряду до різниці потенціалів (напруги) на пластинах:

.

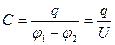Ємність плоского конденсатора:

,

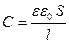де 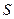– площа його пластин, 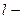відстань між обкладками, 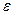– діелектрична проникність середовища, яке заповнює конденсатор.

Ємність батареї з 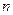конденсаторів, з'єднаних паралельно, дорівнює:

.

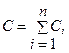Ємність батареї з 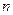конденсаторів, з’єднаних послідовно, визначається співвідношенням:

.

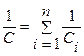Енергія зарядженого конденсатора :

.

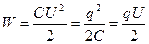Об’ємна густина енергії електричного поля (енергія віднесена до одиниці об’єму) рівна:

.

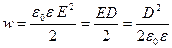Постійний струм

Закони постійного струму

Сила струму вимірюється кількістю електрики, що проходить через поперечний переріз провідника за одиницю часу:

.

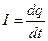Густина струму вимірюється силою струму, що відноситься до одиниці площі поперечного перерізу провідника:

.

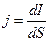Закон Ома для ділянки однорідного (тобто не містить електрорушійних сил) кола:

,

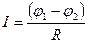де 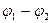- різниця потенціалів на кінцях ділянки, 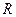– опір ділянки.

Опір провідника довжиною 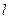з площею поперечного перерізу 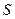рівний:

,

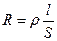де 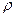- питомий опір матеріалу провідника.

Залежність питомого опору від температури:

,

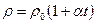де 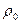– питомий опір при 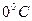, 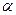– температурний коефіцієнт опору.

Закон Ома для замкненого кола: сила струму в замкнутому колі пропорційна алгебраїчній сумі всіх е.р.с., що діють в колі, і обернено пропорційна його повному опору, рівному сумі опорів зовнішньої і внутрішньої ділянок, тобто:

.

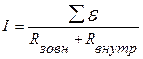Правила Кірхгофа для розгалуджених електричних кіл:

1) алгебраїчна сума сил струму, що сходяться в будь-якому вузлі кола, дорівнює нулю:

;

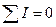2) для будь-якого замкнутого контура алгебраїчна сума добутків сил струмів на опори відповідних ділянок кола дорівнює алгебраїчній сумі всіх е.р.с., діючих в цьому контурі:

.

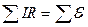Загальний опір ділянок при їх послідовному з'єднанні визначається співвідношенням:

.

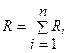Загальний опір ділянок при їх паралельному з'єднанні визначається співвідношенням:

.

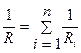Робота електричних сил на ділянці кола, на кінцях якого є різниця потенціалів 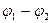, дорівнює:

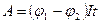, або .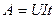

Кількість теплоти, що виділяється на ділянці кола опором 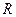, по якій на протязі часу 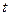проходить струм силою 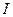, визначається співвідношенням (закон Джоуля-Ленца):

.

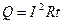Робота, виконана джерелом електричної енергії за час ,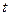

,

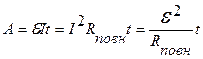де 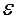− е.р.с. джерела, 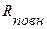− повний опір кола.