Интерференция, дифракционная решетка

Интерференция света - это сложение волн, при котором наблюдается характерное пространственное перераспределение интенсивности (интерференционная картина), например в виде чередующихся светлых и темных полос в случае линейных источников.

Интерференция возникает только в случае если разность фаз волн одинаковой частоты постоянна во времени (когерентные волны).

Простейшим способом получения интерференционной картины от двух линейных источников является метод Юнга, заключающийся в том, что плоская монохроматическая волна направляется на две узкие параллельные щели, за которыми располагается экран. В результате на экране, расположенном за щелями будет наблюдаться интерференционная картина в виде чередующихся темных и светлых интерференционных полос (при условии, что расстояние между щелями много больше расстояния от щелей до экрана).

Принципиальная схема опыта изображена на Рис. 1.23.

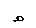
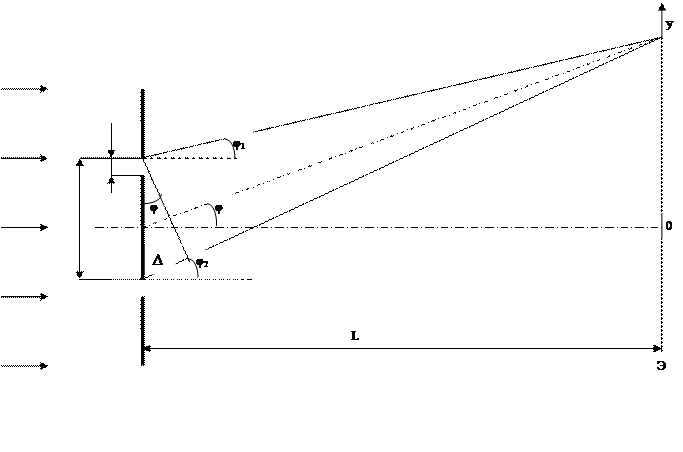
Рис. 1.23

Согласно принципу Гюйгенса, плоскости щелей становятся источниками S₁ и S₂ вторичных волн, распространяющихся во все стороны, т.е. свет дифрагирует на щелях. Дифрагированные волны являются когерентными, т.к. они образовались путем деления фронта падающей волны. Следовательно, они могут интерферировать в области их наложения, что наблюдается на экране Э, находящемся на расстоянии L от плоскости щелей. Вышеописанная дифракция наблюдается только в параллельных пучках, поэтому в принципиальной схеме должны выполняться условия L >> b и L>>d, где b – ширина щелей,d – расстояние между их центрами. В этом случае лучи, идущие к экрану, будут практически параллельными, а углы φ₁ и φ₂ на рис. 4.20 практически будут равны (φ₁=φ₂=φ).

Распределение интенсивности на экране получим, если учтем, как распределение интенсивности из-за взаимной интерференции когерентных волн идущих от щелей, так и распределение интенсивности из-за дифракции на каждой щели.

Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. главные минимумы интенсивности, обусловленные дифракцией, будут наблюдаться в направлениях, определяемых условием дифракционного минимума для одной щели:

b sin φ = ± mλ (m = 1, 2, 3, …), (1.42)

где φ – угол дифракции (Рис. 1.23).

Определим условия возникновения интерференционных минимумов и максимумов, для чего найдем разность хода Δ лучей, идущих от обеих щелей (см. рис. Рис. 1.23).

∆=d sin φ. (1.43)

Здесь d – расстояние между серединами щелей.

Вследствие взаимной интерференции световых лучей, посылаемых щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы. Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода Δ лучей равная λ / 2, 3λ / 2 и т.д.Таким образом, условие дополнительных интерференционных минимумов

d sin φ=± (2m + 1) 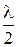(m = 0,1,2,…,) (1.44)

Наоборот, действие одной щели будет усиливать, вследствие интерференции, действие другой, если Δ = λ, 2λ, 3λ . . .:

d sin φ_m=± 2m 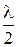=±mλ,(m = 0,1,2,…,) (1.45)

т.е. выражение (1.45) задает условие главных интерференционных максимумов.

Таким образом, полная дифракционная картина для двух щелей определяется из условий:

b sin φ=±λ, ±2 λ, ±3 λ,… (1.46)

- главные дифракционные минимумы;

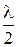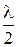d sin φ= ± , ±3 , ±5 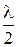,…, (1.47)

- дополнительные интерференционные минимумы;

d sin φ=0, ±λ, ±2 λ, ±3 λ,… (1.48)

- главные интерференционные максимумы,

Результирующее распределение интенсивности на экране Э дано на Рис. 1.24.

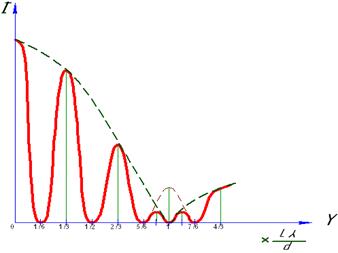
Рис.1.24

Пунктирная кривая соответствует распределению первичных дифракционных максимумов и минимумов, сплошная – результирующему распределению с учетом интерференции. График показывает, что почти весь дифрагированный световой поток (~90%) сосредоточен в пределах 0-го главного максимума. Если d больше b, то в пределах главного максимума уложится несколько интерференционных максимумов. Сужение щелей приводит к тому, что центральный максимум расширяется, при этом, как показывает опыт, интенсивность уменьшается. Наоборот, чем шире щели, тем картина ярче, но максимумы уже, а их число - больше.

Определим линейные координаты y максимумов и минимумов, наблюдаемых на экране. Учитывая малость угла φ, имеем φ₁=φ₂≈φ и тогда, как видно из рис.4.20

y = Ltgφ ≈ Lsinφ

Тогда, условия (1.46-4.48) запишутся так:

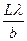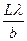y_min= ±; ±2; ±3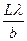;…; - главные дифракционные минимумы.

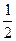
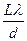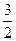
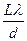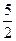
y_min=± ; ± ; ± ;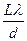…;-дополнительные интерференционные минимумы.

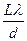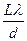y_max= 0; ±; ±2; ±3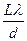;…; - главные интерференционные максимумы.

Картина зависимости интенсивности от расстояния y, выраженного в долях Lλ/b, приведена на Рис.1.24. При этом выполняется условие d = 3b. Тогда предыдущие равенства запишутся:

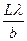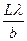y_min= ±; ±2; ±3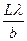;…; - главные дифракционные минимумы.

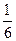
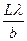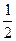
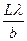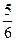
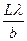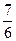
y_min= ± ; ± ; ± ; ± ;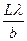…; - дополнительные интерференционные минимумы.

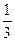
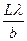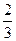
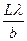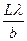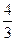
y_max= 0; ± ; ± ; ±; ± ;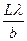…; - главные интерференционные максимумы.

Как видно из рисунка 1.24, интерференционные полосы с координатами максимумов ±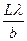оказываются «разорванными» вследствие совпадения этих координат с координатами главных дифракционных минимумов.

Шириной интерференционной полосы∆х называется расстояние между серединами соседних главных максимумов или минимумов. Его легко можно найти из Рис.1.25. Например, для второй и третьей полос имеем:

Δx=( - ) = ,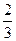

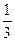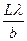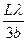или для нашего конкретного примера, учитывая, что 3b = d:

∆x=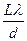

Дифракционная решетка(одномерная) представляет собой систему параллельных равноотстоящих друг от друга щелей равной ширины. Расстояние между соседними щелями называется периодом или постоянной решетки d.

Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие (1.44), условием главных максимумов - условие (1.45), а условием дополнительных минимумов - условие аналогичное условию (1.48)

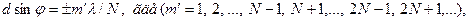(1.49)

Здесь т' может принимать все целочисленные значения, кроме 0, N, 2N, .... т. е. кроме тех, при которых условие (1.45) переходит в (1.44). Следовательно, в случае N щелей между двумя главными максимумами располагается N- 1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.

Чем больше щелей N, тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интенсивными и более острыми будут максимумы. На Рис.1.25 качественно представлена дифракционная картина от восьми щелей. Так как модуль sinjне может быть больше единицы, то из (1.45) следует, что число главных максимумов

,

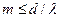т. е. определяется отношением периода решетки к длине волны.

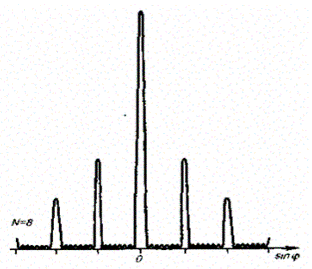
Рис.1.25

Положение главных максимумов зависит от длины волны l (см. (1.45)). Поэтому при пропускании через решетку белого света все максимумы, кроме центрального (m = 0), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная - наружу. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов). Поэтому дифракционная решетка используется в качестве основного элемента многочисленных спектральных приборов.

Дифракционные решетки, используемые в различных областях спектра, отличаются размерами, формой, материалом поверхности, профилем штрихов и их частотой (от 6000 до 0,25 штрих/мм, что позволяет перекрывать область спектра от ультрафиолетовой его части до инфракрасной). Например, ступенчатый профиль решетки позволяет концентрировать основную часть падающей энергии в направлении одного определенного ненулевого порядка.

Основными характеристиками решеток являются их разрешающая способность и дисперсия.

Разрешающая способность дифракционной решетки 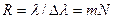, где 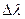- минимальная разность длин волн соседних линий в спектре, которые еще разрешаются решеткой.

Дисперсия дифракционной решетки 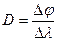, где 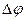- угловое расстояние между двумя соседними спектральными линиями, различающимися на .

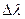Дифракция рентгеновских лучей (λ ~ 10^-10м) на кристаллической решетке (d ~ 10^-10м) позволяет проводить структурный анализ кристаллов, пользуясь формулой Вульфа - Брегга:

.

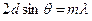где d - расстояние между атомными плоскостями кристалла;

θ - угол отражения лучей от атомных плоскостей;

m = 1, 2, 3, ... порядок дифракционного максимума.

На законах интерференции и дифракции света основана голография- оригинальный способ записи и последующего воспроизведения волнового поля.