Приклади розв'язання задач. Задача 3.1.Під час циклу Карно газ, набравши від нагрівача 103 Дж тепла, виконав роботу 400 Дж

Задача 3.1.Під час циклу Карно газ, набравши від нагрівача 10³ Дж тепла, виконав роботу 400 Дж. Знайти температуру нагрівача, якщо температура холодильника 0 °С.

Рішення.ККД ідеальної теплової машини

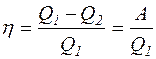або

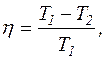
де 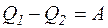- корисне тепло, що перетворюється в роботу А.

Числове значення ККД теплової машини

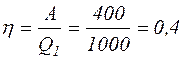або 40%.

Знаючи ККД теплової машини і температуру холодильника Т₂, можна знайти температуру нагрівача

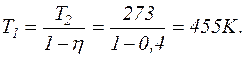
Відповідь: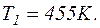

Задача 3.2.Визначити зміну ентропії при ізотермічному розширенні кисню масою 10 г від об'єму 25 л до об'єму 100 л.

Рішення.Зміну ентропії кисню при ізотермічному процесі можна обчислити за формулою

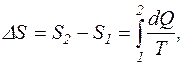
винесемо температуру за знак інтегралу, отримаємо

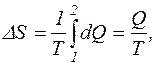
Кількість теплоти 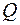, яку отримує кисень, знайдемо за першим законом термодинаміки:

Для ізотермічного процесу = 0, тобто = А, а робота А для цього процесу визначається за формулою

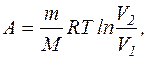
де М= 18×10 ³ кг/моль - молярна маса кисню.

З урахуванням цієї формули, визначимо зміну ентропії

.

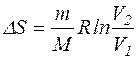Підставляючи в останню формулу числові значення величин, взятих в одиницях системи СІ, маємо

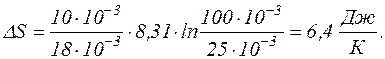
Відповідь: 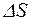= 6,4 Дж/К.

Задача 3.3.Знайти зміну ентропії при охолодженні 2 г повітря від 40 до 0 °С: 1). при сталому об'ємі; 2). при сталому тиску.

Рішення.Зміну ентропії повітря наближено можна обчислити за формулою, що виражає зміну ентропії ідеального газу

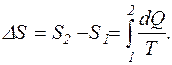
при нескінченно малій зміні температури dT.

При нагріванні подається кількість теплоти

dQ=mcdT,

де т - маса повітря; с - його питома теплоємність.

Враховуючи, що V= const, VdP = RdT, звідки

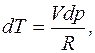
а також із рівняння стану ідеального газу 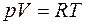знаходимо 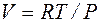. підставивши ці значення у рівняння для dQ, знаходимо

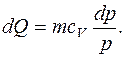
Аналогічно знаходимо значення dQ для сталого тиску

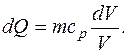
У першому випадку сталим лишається об'єм, тому

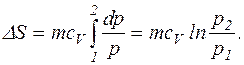
Відношення Р₂/Р₁ знаходимо за рівнянням ізохоричного процесу

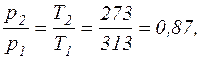
тоді

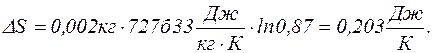
У другому випадку сталим лишається тиск, тому

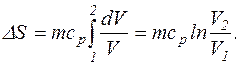
Відношення V₂/V₁ знаходимо за рівнянням ізобаричного процесу

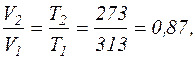
тоді

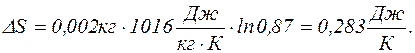
Відповідь:1) 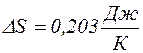; 2)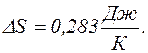

Задача 3.4.Обчислити, користуючись рівнянням Ван-дер-Ваальса, тиск 1,1 кг вуглекислого газу, що знаходиться в балоні місткістю 20 л при температурі 13 °С. Результат порівняти з тиском ідеального газу за тих самих умов.

Рішення.Рівняння Ван-дер-Ваальса має вигляд

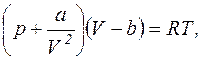
звідки

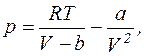
де а=0,364 м⁴×Н/моль²; b=4,3×10^-5 м3/моль.

Число молів вуглекислого газу дорівнює

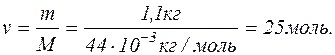
Об'єм, що його займає один моль вуглекислого газу, дорівнює

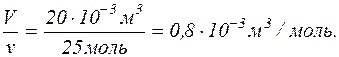
Підставивши у формулу тиску числові значення величин, взятих в одиницях системи СІ, знаходимо

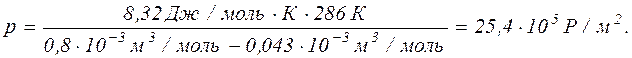
Тиск, що обчислюється за рівнянням Менделєєва-Клапейрона, дорівнює

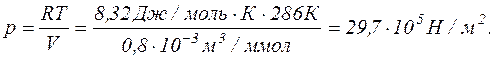
Останній результат відрізняється від результату, одержаного при врахуванні поправок а та b на величину 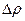= 4,3 • 10⁵ Н/м ², що дає відносну похибку

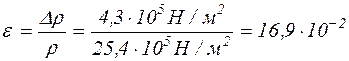або 16,9 %.