Приклади розв’язування задач. Задача 1.1. Визначити для сірчаної кислоти: 1) відносну молекулярну масу Мr; 2) молярну масу M

Задача 1.1. Визначити для сірчаної кислоти: 1) відносну молекулярну масу М_r; 2) молярну масу M.

Рішення. 1. Відносна молекулярна маса речовини дорівнює сумі відносних атомних мас всіх елементів, атоми яких входять до складу молекули даної речовини, і визначається по формулі

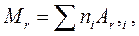(1)

де n_i — число атомів 1-го елемента, що входять у молекулу;

A_r,i — відносна атомна маса 1-го елемента.

Хімічна формула сірчаної кислоти має вид H₂SO₄. Так як до складу молекули сірчаної кислоти входять атоми трьох елементів, то сума, що стоїть в правій частині, рівності (1) буде складатись з трьох складових та вона прийме вигляд

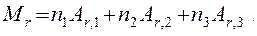(2)

З формули сірчаної кислоти далі виходить, що п₁=2 (два атоми водню), n₂=1 (один атом сірки) та n₃=4 (чотири атоми кисню).

Значення відносних атомних мас водню, сірки і кисню знайдемо в таблиці Д.І. Менделєєва.

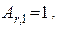
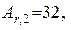
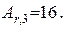
Підставивши значення n_i, та A_r,i у формулу (2), знайдемо (відносну молекулярну масу сірчаної кислоти:

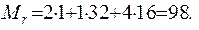
2. Знаючи відносну молекулярну масу М_r, знайдемо молярну масу сірчаної кислоти по формулі

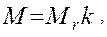(3)

де k=10^-3кг/моль.

Підставивши в (3) значення величин отримаємо

М = 98-10^-3 кг/моль.

Відповідь:М = 98-10^-3 кг/моль.

Задача 1.2. Визначити молярну масу М суміші кисню масою m₁=25 г і азоту масою m₂=75 г.

Рішення. Молярна маса суміші М є відношенням маси суміші т докількості речовини суміші v:

M = m/v. (1)

Маса суміші дорівнює сумі мас компонентів суміші:

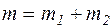(2)

Кількість речовини суміші дорівнює сумі кількостей речовини компонентів:

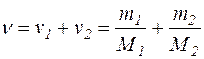. (3)

Підставивши у формулу (1) рівняння (2) і (3) , отримаємо:

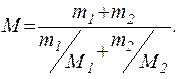(4)

Застосувавши метод, використаний у задачі 1.1, знайдемо полярні маси кисню M₁ і азоту М₂: M₁=32 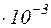кг/моль; М₂=28 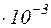кг/моль.

Підставимо значення величин в рівняння (3)та зробимо розрахунки:

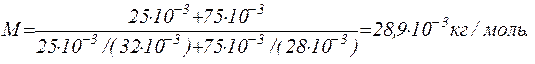
Відповідь: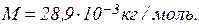

Задача 1.3. Визначити число N молекул, що містяться в об’ємі V=1 мм³ води, і масу m₁ молекули води, Вважаючи умовно, що молекули води мають вид кульок, що стикаються одна з одною, знайти діаметр d молекул.

Рішення. Число N молекул, що містяться в деякій системі масою т, дорівнює добутку постійної Авогадро N_A на кількість речовини v:

.

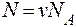Так як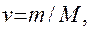

де M - молярна маса, звідси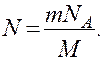

Вказавши з цієї формули масу як добуток густини на об’єм V отримаємо

.

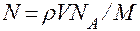Зробимо обчислення, враховуючи, що M=18 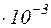кг/моль:

.

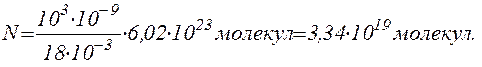Масу т₁ однієї молекули можна знайти по формулі

m₁ = M/N_A. (1)

Підставивши у (1) значення M та N_A знайдемо масу молекули води:

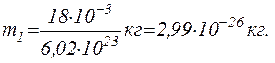
Якщо молекули води щільно прилягають друг до друга, то можна вважати, що на кожну молекулу приходиться об’єм (кубічна ячейка) V₁=d³, де d — діаметр молекули. Звідси

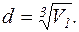(2)

Обсяг V₁ знайдемо, розділивши молярний об’єм V_m на число молекул в молі, тобто на N_а:

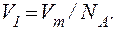(3)

Підставимо рівняння (3) в (2):

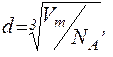
де 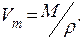Тоді

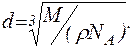(4)

Перевіримо, чи дає права частина рівняння (4) одиницю довжини:

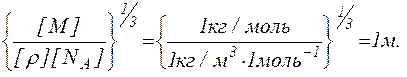
Зробимо обчислення:

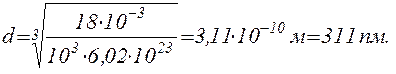
Відповідь: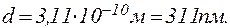

Задача 1.4. В балоні об’ємом 10 л знаходиться гелій під тиском p₁ = 1 МПа та при температурі T₁ = 300 К. Після того як з балона було взято m=10г гелію, температура в балоні понизилася до T₂ = 290K. Визначити тиск p₂ гелію, що залишився в балоні.

Рішення. Для вирішення задачі скористаємося рівнянням Менделєєва -Клапейрона, застосувавши його до кінцевого стану газу:

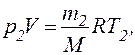(1)

де т₂ — маса гелію в балоні в кінцевому стані; М — молярна маса гелію; R — молярна газова постійна.

З рівняння (1) виразимо шуканий тиск:

p₂=m₂RT₂/(MV). (2)

Масу т₂ гелію виразимо через масу т₁, щовідповідає початковому стану, та масу т гелію, взятого з балону:

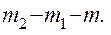(3)

Масу m₁гелію знайдемо також з рівняння Менделеєва - Клайперона, застосувавши його до початкового стану:

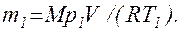(4)

Підставивши рівняння маси m₁ в (3), а потім рівняння m₂ в (2), знайдемо

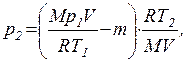
чи

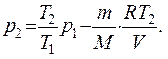(5)

Перевіримо, чи дає формула (5) одиницю тиску. Для цього в її праву частину замість символів величин підставимо їхньої одиниці. В правій частині формули два; доданки. Очевидно, що перше з них дає одиниць тиску, тому що складається з двох множників, перший з який (T₂/T₁) — безрозмірний, а другий — тиск. Перевіримо другий доданок:

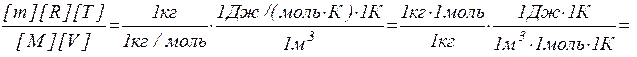
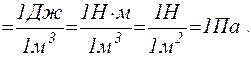
Паскаль є одиницею тиску. Зробимо обчислення по формулі (5), враховуючи, що M= 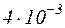кг/моль:

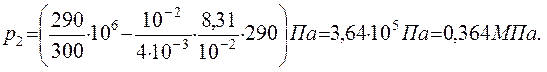
Відповідь: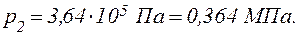

Задача 1.5.Балон містить т₁ = 80 г кисню і m₂ = 320 г аргону. Тиск суміші р= 1 МПа, температура T=300К. Приймаючи дані гази за ідеальні, визначити об’єм V балона.

Рішення. За законом Дальтона, тиск суміші дорівнює сумі парціальних тисків газів, що входять до складу суміші. По рівнянню Менделєєва — Клапейрона, парціальні тиски р₁ кисню і р₂аргону виражаються формулами

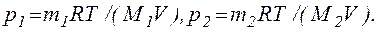
Звідси за законом Дальтона тиск суміші газів

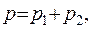
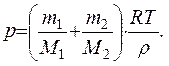
Зробимо обчислення, враховуючи, що :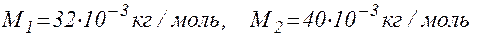

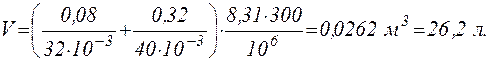
Відповідь: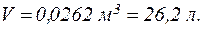

Задача 1.6. Знайти середню кінетичну енергію <e_вр> обертального руху однієї молекули кисню при температурі T=350 K, а також кінетичну енергію E_k обертального руху всіх молекул кисню масою m = 4 г.

Рішення. На кожен ступінь волі молекули газу приходиться однакова середня енергія e = 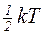, де k — постійна Больцмана; Т — термодинамічна температура газу.

Так як обертальному руху двохатомної молекули (молекула кисню-двохатомна) відповідають дві ступені волі, то середня енергія обертального руху молекули кисню

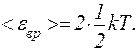(1)

Кінетична енергія обертального руху всіх молекул газу

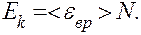(2)

Число всіх молекул газу

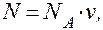(3)

де, 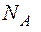- постійна Авогадро;

v-кількість речовини.

Якщо врахувати, що кількість речовини v=m/M, де т — маса газу; М — молярна маса газу, то формула (3) прийме вигляд

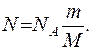
Підставивши рівняння N в формулу (2), отримаємо

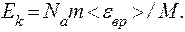(4)

Зробимо обчислення, враховуючи, що для кисню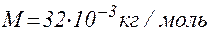

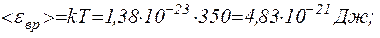
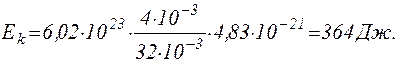
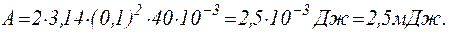
Відповідь: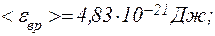

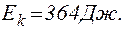
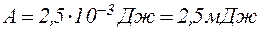
Запитання для самоконтролю

1. Який газ називається ідеальним?

2. Сформулювати закони ідеального газу, записати їх рівняння та нарисувати їх графіки.

3. Вивести рівняння газового стану для ідеального газу.

4. За яких умов властивості реальних газів наближаються до властивостей ідеального газу?

5. Як виводиться основне рівняння молекулярно-кінетичної теорії газів?

6. Як експериментально визначають швидкості молекул газу?

7. У чому полягає закон Максвела про розподіл швидкостей молекул та якими дослідами він підтверджується?