Електростатика

· Закон збереження електричного заряду: в електрично ізольованій системі алгебраїчна сума зарядів усіх частинок – величина стала:

.

· Закон Кулона: два точкові заряди q₁ i q₂, що розміщені у вакуумі на відстані r, взаємодіють із силою:

,

де Ф/м – електрична стала в системі СІ.

· Напруженість електричного поля – векторна величина:

,

де F – сила, яка діє на внесений в дану точку поля позитивний заряд q_0.

· Потенціал електричного поля – скалярна величина:

, ,

де W_n – потенціальна енергія пробного заряду q₀ (при умові, що потенціальна енергія заряду в нескінченності дорівнює нулю, ), – робота переміщення заряду q₀ з даної точки в .

· Потенціальна енергія взаємодії двох точкових зарядів q₁ і q₂, що розміщені на відстані r однин від одного:

,

при умові, що

· Робота переміщення заряду q в електричному полі з точки 1 в точку 2:

; ,

де – елемент переміщення; 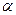– кут між і ; – різниця потенціалів (напруга) між точками 1 і 2.

· Зв’язок між напруженістю електричного поля і різницею потенціалів:

,

де береться в напрямку найбільш швидкої зміни потенціалу, тобто вздовж силової лінії.

· Для однорідного поля ( ):

,

де 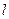– відстань між двома точками, виміряна в напрямку силової лінії.

· Лінійна густина заряду – кількість заряду, що припадає на одиницю довжини:

.

· Поверхнева густина заряду – кількість заряду, що припадає на одиницю площі:

.

· Об’ємна густина заряду 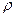– кількість заряду, що припадає на одиницю об’єму:

.

· Напруженість і потенціал електричного поля, яке створене точковим зарядом q на відстані r від нього:

.

· Напруженість і потенціал поля, яке створене системою точкових зарядів (принцип суперпозиції електричних полів):

– геометрична сума;

– алгебраїчна сума.

· Напруженість і потенціал поля, яке створене рівномірно розподіленим зарядом вздовж тонкого стержня:

де – радіус-вектор, що направлений від виділеного елемента dl до точки, в якій визначається напруженість або потенціал; – лінійна густина заряду.

· Потік вектора напруженості крізь поверхню S:

,

де – проекція вектора на напрям додатної нормалі до елемента площі ds.

· Теорема Остроградського-Гаусса: потік вектора крізь довільну замкнену поверхню дорівнює алгебраїчній сумі зарядів, що охоплені цією поверхнею, поділеній на :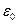

.

· Напруженість поля, яке створене нескінченно великою рівномірно зарядженою площиною:

де 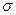– поверхнева густина заряду.

· Напруженість поля, яке створене двома нескінченно великими паралельними, рівномірно зарядженими площинами з поверхневою густиною заряду i , в точках, що розміщені між площинами і зовні їх, відповідно:

Е_зовні = 0.

· Напруженість поля, яке створене рівномірно зарядженою сферичною поверхнею в точках, що розміщені всередині і зовні сфери на відстані r від її центра

Е = 0, Е_зовні = ,

де q – заряд сфери.

· Напруженість поля, яке створене нескінченно довгою рівномірно зарядженою ниткою, або нескінченно довгим рівномірно зарядженим циліндром в точках, що розміщені зовні його поверхні і всередині:

, Е_{всеред.} = 0,

де a – відстань точки від нитки (осі циліндра).

· Електричний момент диполя (дипольний момент):

,

де 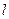– плече диполя – векторна величина, направлена від негативного заряду до позитивного і дорівнює відстані між зарядами.

· Вектор поляризації для ізотропного діелектрика:

де – діелектрична сприйнятливість діелектрика; – напруженість електричного поля всередині діелектрика.

· Зв’язок між векторами поляризації і поверхневою густиною зв’язаних

зарядів :

,

де – проекція вектора на зовнішню нормаль до поверхні діелектрика.

· Зв’язок між векторами електричного зміщення (електричною індукцією) і напруженістю електричного поля :

,

де 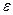– діелектрична проникність середовища .

· Потенціальна енергія диполя в зовнішньому полі:

.

· Теорема Остроградського-Гаусса для електричного поля в діелектрику: потік вектора електричного зміщення крізь довільну замкнену поверхню дорівнює алгебраїчній сумі зарядів, що охоплені цією поверхнею:

де 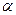– кут між вектором електричного зміщення і додатною нормаллю до елемента поверхні dS.

· Електроємність відокремленого провідника і конденсатора:

, ,

де – потенціал провідника; U – різниця потенціалів (напруга) на пластинах конденсаторах.

· Електроємність плоского конденсатора:

де S – площа кожної пластини (обкладки) конденсатора; d – відстань між пластинами; 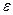– діелектрична проникність середовища, яке заповнює простір між пластинами конденсатора.

· Електроємність циліндричного конденсатора:

де h – висота коаксіальних циліндрів; r і R – радіуси внутрішнього і зовнішнього циліндрів відповідно.

· Електроємність сферичного конденсатора:

,

де r i R – радіуси внутрішньої і зовнішньої сфер відповідно.

· Електроємність ізольованої сфери, радіус якої R:

,

де 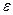– діелектрична проникність середовища, в якому розміщена сфера.

· Електроємність системи (батареї) конденсаторів:

– при послідовному з’єднанні;

– при паралельному з’єднанні,

де N – кількість конденсаторів у батареї.

· Енергія зарядженого конденсатора:

.

· Об’ємна густина енергії 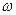електричного поля (енергія, що припадає на одиницю об’єму):

.

· Сила взаємного притягання пластин конденсатора:

.

8.1. Дві однакові заряджені металеві кульки = 0,2 нКл і = - 0,6 нКл внаслідок притягання зіткнулись і знову розійшлись на відстань 5 см. Визначити заряд кожної кульки після зіткнення і силу взаємодії між ними.

8.2. Який заряд мають дві однаково заряджені краплі води, радіус яких r = 7,6∙10^{-5 м}, якщо сила взаємного гравітаційного притягання їх врівноважується силою кулонівського відштовхування ? Краплі вважати матеріальними точками.

8.3. Два точкові заряди = 1,67 нКл і = 3,33 нКл розміщені на відстані 20 см один від одного. У якій точці на прямій лінії, проведеній через обидва заряди, треба розмістити третій точковий заряд = - 0,67 нКл, щоб він був у рівновазі ? Масами зарядів знехтувати.

8.4. Дві кульки розміщені на відстані 0,1 м одна від одної, мають однакові негативні заряди й взаємодіють із силою 0,23 мН. Визначити кількість “надлишкових” електронів на кожній кульці.

8.5. Відстань між зарядами = 100 нКл і = - 50 нКл дорівнює 10 см. Визначити силу, яка діє на заряд = 1 мкКл, що розміщений на відстані 12 см від заряду і на відстані 10 см від заряду .

8.6. У вершинах квадрата розміщено однакові однойменні заряди q = 2,3 нКл. Який заряд треба розмістити в центрі квадрата, щоб результуюча сила, яка діє на кожний заряд, дорівнювала нулю?

8.7. Дві однакові металеві кульки підвішені в одній точці на шовкових нитках довжиною l = 20 см. Після надання кулькам заряду 0,4 мкКл нитки розійшлися на кут 60 . Визначити масу кожної кульки.

8.8. Три однакові кульки масою m = 0,1 г кожна підвішені в одній точці на шовкових нитках довжиною l = 20 см. Які однакові заряди треба надати кулькам, щоб кожна нитка утворювала з вертикаллю кут a = 30 ?

8.9. Обчислити швидкість електрона, який рухається по коловій орбіті в атомі водню, якщо радіус орбіти дорівнює 0,5·10 см.

8.10. Навколо нерухомого точкового заряду q, в одній площині з ним, обертається підвішена на нитці довжиною l = 1,2 м кулька масою m = 2 г і зарядом q. Визначити заряд кульки, якщо її період обертання T = 3,2 с, а кут відхилення від вертикалі a = 25 .

8.11. В однорідному електричному полі з напруженістю Е = 1,5 кВ/м, що напрямлена вертикально вниз, рівномірно обертається кулька, масою m = 1 г і зарядом q = 0,2 мкКл. Кулька підвішена на нитці, довжиною l = 20 см. Кут відхилення нитки від вертикалі α = 30⁰. Визначити період обертання і силу натягу нитки.

8.12. Тіло масою m = 3 г і зарядом q = 10 мКл, підвішене на невагомій нитці, відхиляють на кут α = 90⁰ від вертикалі і відпускають. Визначити натяг нитки в момент, коли нитка утворює кут β = 60⁰ з вертикаллю. Тіло перебуває в однорідному, напрямленому вертикально вгору електричному полі з напруженістю Е = 1 кВ/м.

8.13. Дві однойменно заряджені однакові кульки, підвішені на нитках однакової довжини, опускають в гас. Якою повинна бути густина матеріалу кульок, щоб кут розходження в повітрі і гасі був той самий? Густина гасу ρ = 800 кг/м³, діелектрична проникність гасу ε = 2.

8.14. Визначити напруженість електричного поля посередині між точковими зарядами = 8 нКл і = - 6 нКл, якщо відстань між зарядами дорівнює 10 см.

8.15. Два однакові позитивні точкові заряди розміщено на відстані 10 см один від одного. Визначити точку на осі симетрії цих зарядів, у якій напруженість електричного поля має максимальне значення.

8.16. Визначити, на скільки зміститься відносно ядра площина колової орбіти електрона в атомі водню, якщо його помістити в електричне поле з напруженістю Е = 200 кВ/м. Вважати, що відстань від ядра до електрона дорівнює R = 0,5·10^{-10 м} і не змінюється при накладанні поля.

8.17. Дві кульки зарядами = 6,7 нКл і = 13,3 нКл розміщено на відстані 40 см одна від одної. Яку роботу треба виконати, щоб наблизити їх до відстані 25 см ?

8.18. Електричне поле створюється двома точковими зарядами = 3 мкКл і = - 2 мкКл, що розміщені на відстані a = 0,1 м один від одного. Визначити роботу сил поля при переміщенні заряду = 0,5 мкКл з точки 1 в точку 2 (рис. 8.1).

8.19. Куля радіусом 5 см заряджена до потенціалу 150 В. Визначити потенціал і напруженість у точці поля, віддаленій від поверхні кулі на 10 см. Рис. 8.1

8.20. Дві однакові кульки масою 0,04 г і радіусом R = 1 см підвішено на шовкових нитках однакової довжини так, що їх поверхні торкаються одна одної. Після того, як кульки зарядили однаковими за величиною електричними зарядами, вони розійшлися на деякий кут і натяг ниток став дорівнювати Т = 490 мкН. Визначити потенціал заряджених кульок, коли відомо, що відстань від точки підвісу до центра кожної кульки дорівнює 10 см.

8.21. У вершинах квадрата розміщено точкові заряди = 10,33 нКл, = - 0,66 нКл, = 0,99 нКл і = - 1,32 нКл. Обчислити потенціал у центрі квадрата, якщо його діагональ дорівнює 20 см.

8.22. Відстань між двома точковими зарядами = 1 нКл і = - 2 нКл дорівнює 10 см. Визначити напруженість і потенціал поля в точці, що розміщена на відстані 9 см від позитивного заряду і 7 см від негативного заряду.

8.23. Ромб утворений із двох рівносторонніх трикутників зі стороною, довжина якої дорівнює 0,2 м. У вершинах при гострих кутах ромба розміщені однакові позитивні заряди q₁= q₂ = 6·10^-7 Кл. У вершині при одному із тупих кутів розміщений негативний заряд q₃= - 8·10 Кл. Визначити напруженість і потенціал електричного поля в четвертій вершині ромба.

8.24. У простір, де одночасно діють горизонтальне і вертикальне однорідні електричні поля, напруженості яких дорівнюють Е_г = 4∙10² В/м і Е_в = 3∙10² В/м, уздовж напрямку вектора напруженості результуючого поля влітає електрон, швидкість якого після проходження шляху l = 2,7 мм зменшилась у 2 рази. Визначити швидкість електрона в кінці його шляху.

8.25. Вісім сферичних крапель ртуті однакового радіусу заряджено до потенціалу φ = 12 В кожна. Всі ці краплі зливаються в одну велику сферичну краплю. Обчислити потенціал великої краплі.

8.26. Дві металеві кулі з радіусами R₁ = 4 см і R₂ = 6 см, що заряджені до потенціалу φ₁ = 9 кВ і φ₂ = 3 кВ відповідно, з’єднують тонким дротом. Визначити густину заряду на поверхні куль після з’єднання.

8.27. Пилинка вагою 10 г розміщена між пластинами плоского горизонтального конденсатора, до якого прикладена напруга 5000 В, віддаль між пластинами 5 см. Який заряд пилинки, якщо вона зависає в повітрі?

8.28. Між двома пластинами, розташованими горизонтально в вакуумі на відстані 4,8 мм одна від одної, перебуває в рівновазі негативно заряджена крапля масла, маса якої 10 нг. Скільки надлишкових електронів має крапля, якщо на пластини подано напругу U = 1 кВ ? Після опромінення крапля почала рухатися вниз з прискоренням а = 6 м/с². Скільки електронів втратила крапля ?

8.29. У плоскому горизонтально розміщеному конденсаторі, відстань між пластинами якого d = 1 см, перебуває заряджена масляна кулька. При відсутності електричного поля кулька падає з постійною швидкістю = 0,1 мм/с. Якщо до пластин прикласти різницю потенціалів U = 200 В, то кулька падає зі швидкістю = 0,5 мм/с. Визначити радіус кульки і її заряд. Коефіцієнт в’язкості повітря h = 1,85·10 Па·с, густина масла більша за густину повітря на r = 0,9·10 кг/м .

8.30. Обчислити потенціальну енергію системи чотирьох точкових зарядів, розміщених у вершинах квадрата зі стороною a = 0,1 м. Заряди однакові за абсолютною величиною = 3 мкКл. Розглянути випадки, коли: 1) всі заряди однойменні; 2) два заряди позитивні, а два – негативні.

8.31. Яку роботу треба виконати, щоб перенести точковий заряд q = 6 нКл із нескінченності в точку, розміщену на відстані l = 10 см від поверхні металевої кульки, потенціал якої φ = 200 В, а радіус R = 2 см ?

8.32. Яку швидкість має електрон, що пролетів прискорюючу різницю потенціалів 200 В?

8.33. Кулька масою 1 г і зарядом 10 Кл рухається з точки А, потенціал якої 600 В, в точку В, потенціал якої дорівнює нулю. Визначити швидкість кульки в точці А, якщо в точці В її швидкість дорівнювала 20 см/с.

8.34. Матеріальна точка масою m = 10^{-7 кг}, що має заряд q = 1 мкКл рухається зі швидкістю 3000 м/с. На яку мінімальну відстань вона може наблизитися до точкового заряду q₁ = 10 мкКл?

8.35. Крізь отвір у негативно зарядженій пластині під кутом b = 30 до її площини влітає a - частинка, кінетична енергія якої = 1600 еВ. Частинка “впала” назад на пластину на відстані l = 3 см від отвору. Визначити: 1) потенціал поля пластини в точці максимального віддалення a - частинки від пластини; 2) напруженість поля; 3) максимальне віддалення a - частинки від пластини. Силою тяжіння нехтувати. Вважати, що потенціал пластини дорівнює нулю.

8.36. Електрон в однорідному електричному полі рухається з прискоренням а = 10 м/с . Визначити: 1) напруженість електричного поля; 2) швидкість, яку отримає електрон за час t = 1 мкс свого руху; 3) роботу сил електричного поля за цей час; 4) різницю потенціалів, яку пройде при цьому електрон. Початкова швидкість електрона = 0.

8.37. Електрон, що пройшов відстань 5,3 мм в плоскому конденсаторі від однієї пластини до другої, отримав швидкість 10 м/с. Визначити: 1) різницю потенціалів між пластинами; 2) напруженість електричного поля всередині конденсатора; 3) поверхневу густину заряду на пластинах.

8.38. Електрон влітає в плоский горизонтальний конденсатор паралельно до пластин зі швидкістю 9·10 м/с. Визначити нормальне і тангенціальне прискорення електрона через 10 с після початку його руху в конденсаторі. Різниця потенціалів між пластинами дорівнює 100 В, відстань між пластинами 1 см.

8.39. Електрон з деякою швидкістю влітає в плоский конденсатор паралельно до пластин на однаковій відстані від них. До пластин конденсатора прикладена різниця потенціалів U = 300 В. Відстань між пластинами d = 2 см, довжина конденсатора l = 10 см. Якою може бути максимальна початкова швидкість електрона, щоб електрон не вилетів з конденсатора?

8.40. Електрон влітає в плоский горизонтальний конденсатор паралельно до його пластини зі швидкістю 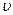= 10 м/с. Напруженість поля в конденсаторі Е = 100 В/см, довжина пластин конденсатора l = 5 см. Визначити величину і напрям швидкості електрона при виході його з конденсатора.

8.41. У простір між пластинами плоского горизонтального конденсатора влітає електрон зі швидкістю 3,6·10 м/с. Вектор швидкості електрона паралельний до пластин конденсатора. Довжина пластин конденсатора 20 см. Напруженість поля всередині конденсатора 37 В/см. На скільки зміститься електрон у вертикальному напрямку під дією електричного поля за час руху в конденсаторі?

8.42. В електронно-променевій трубці потік електронів з кінетичною енергією = 8 кеВ рухається між пластинами плоского горизонтального конденсатора завдовжки х = 4 см, відстань між пластинами d = 2 см. Яку напругу треба подати на пластини конденсатора, щоб електронний пучок, виходячи з конденсатора, змістився у вертикальному напрямку на y = 0,8 см?

8.43. Тонкий стрижень довжиною l = 30 см має рівномірно розподілений заряд з лінійною густиною t = 1 мкКл/м. На відстані r = 20 см від стержня розміщено заряд q = 10 нКл. Заряд рівновіддалений від кінців стержня. Визначити силу взаємодії заряду зі стержнем.

8.44. Тонкий стрижень довжиною l = 20 см має рівномірно розподілений заряд. На продовженні осі стержня на відстані а = 10 см від ближчого його кінця розміщений точковий заряд q = 40 нКл, який взаємодіє зі стрижнем з силою F = 6 мкН. Визначити лінійну густину заряду на стрижні.

8.45. Тонкий півнескінченний стрижень має рівномірно розподілений заряд з лінійною густиною τ = 1,5 нКл/см. На осі стрижня, на відстані d = 12 см від його кінця, розміщений точковий заряд q = 0,2 мкКл. Визначити силу взаємодії стрижня і заряду.

8.46. Рівномірно заряджена тонка нитка, довжина якої l = 20 см, має лінійну густину заряду τ = 10 нКл/м. На відстані а = 10 см від нитки, навпроти її середини, розміщено точковий заряд q = 1 нКл. Яка сила F діє на цей заряд з боку зарядженої нитки?

8.47. В електричне поле, створене довгим рівномірно зарядженим циліндром радіусом R = 1 см з поверхневою густиною заряду σ = 0,3 нКл/см², внесено точковий заряд q = 15 нКл. Визначити силу, з якою поле діє на заряд, якщо відстань від осі циліндра r = 10 см.

8.48. Тонкий стрижень довжиною 10 см має рівномірно розподілений заряд з лінійною густиною t = 10 нК/м. Визначити напруженість і потенціал поля в точці, яка розміщена на продовженні осі стрижня на відстані 10 см від його ближчого кінця.

8.49. Півнескінченний тонкий дріт рівномірно заряджений з лінійною густиною заряду t = 0,1 мкКл/м. Визначити напруженість поля в точці, що лежить на перпендикулярі до кінця дроту на відстані 10 см від нього.

8.50. Електричне поле створено нескінченно довгою зарядженою ниткою з лінійною густиною заряду t = 10 нКл/м. Визначити різницю потенціалів між двома точками, розміщеними від нитки на відстані r₁ = 5 см і r₂ = 10 см.

8.51. Визначити потенціал електричного поля в центрі тонкого зарядженого кільця з лінійною густиною заряду t = 31,8 нКл/м.

8.52. Тонке кільце радіусом R = 8 см має рівномірно розподілений заряд з лінійною густиною заряду t = 10 нКл/м. Визначити напруженість електричного поля в точці, яка рівновіддалена від усіх точок кільця на відстань r = 10 см.

8.53. Тонке кільце радіусом R = 10 см заряджене негативно і має заряд q = - 5 нКл. Визначити напруженість електричного поля Е на осі кільця в точках, які розміщені від центра кільця на відстані L = 0, 5, 8, 10 і 15 см. Побудувати графік Е = f (L). Визначити, на якій відстані L від центра кільця напруженість електричного поля буде максимальною.

8.54. Диск радіусом R = 20 см має рівномірно розподілений по поверхні заряд з поверхневою густиною заряду s = 2 мкКл/м . Визначити напруженість електричного поля в точці, що лежить на нормалі до центра диска на відстані l = 10 см від його центра.

8.55. У центрі металевої сфери радіусом R = 10 см, на якій рівномірно розподілений заряд q = - 20 нКл, розміщено точковий заряд q = 20 нКл. Визначити напруженість електричного поля в точках, що віддалені від центра сфери на відстані r = 10 см і r = 20 см.

8.56. Визначити напруженість Е електричного поля у центрі рівномірно зарядженої півсфери. Поверхнева густина заряду на півсфері σ = 3 нКл/м².

8.57. На деякій відстані від нескінченної рівномірно зарядженої площини, паралельно до неї, розміщено круг радіусом r = 15 см. Обчислити потік Ф_Е вектора напруженості електричного поля крізь круг, якщо поверхнева густина заряду на площині σ = 2 мкКл/м² .

8.58. На відстані а = 30 см від нескінченної рівномірно зарядженої нитки розміщена кругла площадка, радіус якої r = 1 мм (рис. 8.2). Визначити потік Ф_Е вектора напруженості крізь площадку, якщо її площина утворює кут α = 30⁰ з лінією напруженості електричного поля, що проходить через центр площадки. Лінійна густина заряду нитки τ = 30 нКл/м.

Рис. 8.2

8.59. Електричне поле створено нескінченно великою рівномірно зарядженою площиною з поверхневою густиною заряду s = 10 нКл/м . Визначити різницю потенціалів між двома точками поля, одна з яких розміщена на площині, а друга на відстані а = 10 см від неї.

8.60. Точки А і В перебувають на відстанях r₁ = 4 см і r₂ = 12 см від нескінченно великої рівномірно зарядженої площини. Визначити поверхневу густину заряду на площині, якщо різниця потенціалів між точками U = 1200 В.

8.61. Електричне поле створено двома вертикальними нескінченно великими паралельними площинами з поверхневою густиною заряду s = 2 нКл/м і s = - 4 нКл/м . Визначити напруженість поля між площинами і зовні площин. Побудувати графік напруженості електричного поля вздовж прямої, перпендикулярної до площин.

8.62. Дві нескінченно довгі однойменно заряджені дротини з однаковою лінійною густиною заряду Кл/м розміщено на відстані а = 10 см одна від одної. Визначити величину і напрям напруженості поля в точці, що розміщена на відстані 10 см від кожної дротини.

8.63. Є дві металеві концентричні заряджені сфери, радіуси яких R = 5 см і R = 10 см, а заряди q = 20 нКл і q = - 10 нКл відповідно. Визначити напруженість електричного поля в точках, що віддалені від центра сфери на r = 3 см, 8 см і 14 см. Побудувати графік зміни напруженості електричного поля вздовж прямої від центра сфер.

8.64. Точковий заряд q = 0,15 мкКл розміщено в центрі сферичної металевої оболонки, внутрішній і зовнішній радіуси якої відповідно дорівнюють r = 20 см і R = 25 см. Визначити напруженість поля в точках, що перебувають на відстанях r₁ = 10 см і r₂ = 50 см від заряду.

8.65. Електричне поле створено нескінченно довгим рівномірно зарядженим циліндром R = 1 см з лінійною густиною заряду t = 20 нКл/м. Визначити різницю потенціалів між двома точками цього поля, що розміщені на відстанях а = 0,5 см і а = 2 см від поверхні циліндра.

8.66. У вакуумі є скупчення зарядів у формі довгого циліндра радіусом R = 2 см. Об’ємна густина зарядів постійна і дорівнює 2 мкКл/см . Визначити напруженість електричного поля Е в точках, що віддалені від осі циліндра на r = 1 см і r =3 см, а також різницю потенціалів між цими точками. Побудувати графіки Е = f(r) і j = f(r).

8.67. На двох довгих коаксіальних циліндрах радіусами R = 2 мм і R = 4 мм рівномірно розподілені заряди з лінійною густиною заряду t = 0,31 нКл/м і t = - 0,31 нКл/м. Визначити напруженість електричного поля в точках, що віддалені від осі циліндра на відстанях r = 3 мм і r = 6 мм, а також різницю потенціалів між циліндрами.

8.68. З якою силою, що припадає на одиницю площі, відштовхуються дві однойменно заряджені нескінченно великі площини з однаковою поверхневою густиною заряду s = 2 мкКл/м ?

8.69. Біля зарядженої нескінченно великої площини розміщено точковий заряд q = 0,7 нКл. Під дією поля заряд переміщається вздовж силової лінії на відстань 2 см, при цьому виконується робота А = 5 мкДж. Визначити поверхневу густину заряду на площині.

8.70. Визначити роботу сил електростатичного поля при переміщенні заряду q = 10 нКл із точки 1 у точку 2, що розміщені між різнойменно зарядженими нескінченно великими паралельними площинами, відстань між якими дорівнює 0,03 м. Поверхнева густина заряду σ = 0,4 мкКл/м².

8.71. На відстані r = 4 см від нескінченно довгого зарядженого провідника розмістили точковий заряд q = 0,7 нКл. Під дією поля заряд переміщається до відстані r = 2 см і при цьому виконується робота А = 5 мкДж. Визначити лінійну густину заряду провідника.

8.72. Тонкий стержень зігнуто в півколо і рівномірно заряджено з лінійною густиною заряду τ = 20 нКл/м. У центрі півкола розмістили точковий заряд q = 1 нКл. Яку роботу потрібно виконати для переміщення заряду з центра півкола в нескінченність?

8.73. Яка робота виконується при перенесенні точкового заряду q = 2·10^-8 Кл з нескінченності в точку, що розміщена на відстані 1 см від поверхні сфери радіусом 1 см з поверхневою густиною заряду σ = 1 нКл/см² ?

8.74. Точковий заряд q = 50 нКл розміщено на відстані 10 см від великої тонкої металевої пластини. Яку роботу потрібно виконати, щоб перенести цей заряд від пластини на нескінченність ?

8.75. Внаслідок зіткнення молекул повітря з космічною частинкою біля від’ємно зарядженої пластини плоского конденсатора утворився електрон. Заряд пластини 2 нКл, її площа 60 см . З якою швидкістю електрон наблизиться до позитивно зарядженої пластини, якщо відстань між пластинами 5 мм ?

8.76. До вертикальної нескінченно великої площини з поверхневою густиною заряду s = 4 нКл/см підвішено на шовковій нитці кульку масою m = 1 г і зарядом q = 1 нКл. Визначити кут відхилення нитки від площини.

8.77. Кулька масою m = 1 г підвішена на нитці довжиною l = 15 см і здійснює коливання за законом математичного маятника над горизонтальною, нескінченно великою, рівномірно зарядженою площиною з поверхневою густиною заряду s = 4 нКл/см . Визначити період коливань кульки, якщо заряд кульки q = - 1 нКл.

8.78. Електричне поле створено позитивно зарядженою нескінченно довгою дротиною з лінійною густиною заряду τ = 2 нКл/см. Яку швидкість отримає електрон, рухаючись до дротини з відстані в 1 см до 0,5 см від дротини?

8.79. Електричне поле створено позитивно зарядженою нескінченною довгою дротиною. Переміщаючись під дією цього поля з точки, що віддалена від дротини на відстані х = 1 см, до точки х = 4 см, a - частинка змінила свою швидкість від 2·10 м/с до 3·10 м/с. Визначити лінійну густину заряду дротини.

8.80. В електричному полі, яке створене зарядженою сферою радіусом 10 см, рухається електрон вздовж радіуса між точками, які віддалені від центра сфери на 13 см і 16 см. При цьому швидкість електрона змінюється від 2·10⁵ м/с до 2·10⁶ м/с. Визначити поверхневу густину заряду сфери.

8.81. З поверхні довгого рівномірно зарядженого циліндра радіусом R = 5 см, лінійна густина заряду якого τ = 20 нКл/м, вилітає α - частинка. Визначити кінетичну енергію α - частинки в точці, що розміщена на відстані а = 40 см від поверхні циліндра.

8.82. Електричний диполь розміщено всередині замкненої поверхні. Що можна сказати про потік вектора напруженості електричного поля крізь цю поверхню?

8.83. Визначити напруженість і потенціал електричного поля диполя, електричний момент якого р = 1,2·10¹⁴ Кл∙м, у точці, що лежить на осі диполя на відстані r = 10 см від його центра з боку позитивного заряду.

8.84. Визначити напруженість електричного поля диполя в точці, що лежить на перпендикулярі до плеча диполя на відстані 50 см від його центра, якщо абсолютна величина заряду диполя 1 нКл, а плече диполя дорівнює 5 мм.

8.85. Диполь з електричним моментом р = 2 нКл·м міститься в однорідному електричному полі, напруженість якого Е = 30 кВ/м. Вектор дипольного електричного моменту рутворює кут α = 60⁰ з напрямом силових ліній поля. Визначити роботу, виконану зовнішніми силами під час повертання диполя на кут β = 30⁰.

8.86. Диполь з електричним моментом р = 10 нКл∙м вільно встановився в однорідному електричному полі з напруженістю Е = 50 кВ/м. Визначити зміну потенціальної енергії диполя при його повороті на 90⁰.

8.87. Диполь розміщено в зовнішньому однорідному електростатичному полі напруженістю Е = 3∙10² В/м так, що вісь диполя утворює кут α = 30⁰ з напрямом напруженості поля. Визначити енергію диполя, якщо електричний момент диполя дорівнює р = 4∙10^-9 Кл∙м.

8.88. Металеву ізольовану кульку радіусом R = 10 см зарядили до q = 6 мкКл, а потім її покрили шаром діелектрика товщиною 2 см. Визначити густину зв’язаних зарядів на внутрішній і зовнішній поверхнях діелектрика, якщо діелектрична проникність діелектрика ε = 3.

8.89. В однорідне електричне поле з напруженістю Е = 5 кВ/м внесли металеву пластину площею S = 100 см². Який заряд індукується на кожній її поверхні?

8.90. Визначити поверхневу густину зв’язаних електричних зарядів на поверхні слюдяної пластини завтовшки 0,2 мм, яка заповнює простір між двома різнойменними рівномірно зарядженими паралельними пластинами, якщо різниця потенціалів між паралельними пластинами 400 В.

8.91. Плоский конденсатор, між обкладками якого розміщена скляна пластинка (ε = 6) товщиною 2 мм, заряджений до напруги 200 В. Нехтуючи відстанню між пластинкою і обкладками, визначити поверхневу густину вільних зарядів на обкладках конденсатора, а також поверхневу густину зв’язаних зарядів на склі.

8.92. Простір між пластинами плоского конденсатора заповнений діелектриком (ε = 6). Відстань між пластинами дорівнює 4 мм. На пластини подано напругу 1200 В. Визначити: 1) напруженість поля в діелектрику; 2) поверхневу густину заряду на пластинах конденсатора; 3) поверхневу густину заряду на діелектрику; 4) діелектричну сприйнятливість.

8.93. Провідна кулька радіусом 7 мм міститься в гасі (ε = 2 ) і має заряд q = 11∙10^-9 Кл. Визначити густину зв’язаних зарядів у гасі біля поверхні кульки і повний діючий заряд.

8.94. Потрібно виготовити конденсатор електроємністю в 2,5·10^-4 мкФ. Для цього на парафінований папір завтовшки в 0,05 мм наклеюють з двох сторін тонкі металеві диски. Який повинен бути діаметр цих дисків?

8.95. Плоский конденсатор, віддаль між пластинами якого дорівнює 5 см, заряджено до 200 В і від’єднано від джерела. Яка буде напруга на конденсаторі, якщо його пластини віддалити одну від одної до 10 см?

8.96. Металеву кулю діаметром 40 см, що заряджена до потенціалу 1000 В, з’єднали провідником з другою металевою кулею діаметром 8 см. Визначити, як розподіляться заряди на кулях після їх з’єднання.

8.97. Визначити електроємність пустотілої алюмінієвої кулі масою 200 г, якщо товщина її стінки 2 мм. Густина алюмінію ρ = 2,7·10³ кг/м³.

8.98. Кулька, що заряджена до потенціалу 792 В, має поверхневу густину заряду σ = 3,33·10⁷ Кл/м². Визначити радіус кульки.

8.99. До акумулятора з різницею потенціалів 300 В під’єднано два конденсатори з електроємностями С₁ = 2 пФ і С₂ = 3 пФ. Визначити заряд і напругу на обкладках кожного конденсатора при послідовному і паралельному їх з’єднанні.

8.100. Три послідовно з’єднані конденсатори з електроємностями 1 мкФ, 2 мкФ і 3 мкФ під’єднано до джерела з різницею потенціалів 220 В. Якими будуть заряд і напруга на обкладках кожного конденсатора?

8.101. Два конденсатори з електроємностями С₁= 2 мкФ і С₂ = 3 мкФ мають електричні заряди q₁ = 4∙10^-6 Кл і q₂ = 9∙10^-6 Кл відповідно. Різнойменно заряджені обкладки конденсатора з’єднали між собою. Визначити заряд кожного конденсатора після їх з’єднання.

8.102. Конденсатор електроємністю С₁ зарядили до напруги 500 В і з’єднали паралельно з незарядженим конденсатором електроємністю 4 мкФ. При цьому вольтметр показав 100 В. Визначити електроємність С₁.

8.103. Визначити електроємність системи конденсаторів (рис. 8.3 ), якщо електроємність кожного кондесатора дорівнює 0,5 мкФ.

8.104. Три конденсатори з електроємностями С₁ = 1 мкФ, С₂ = 2 мкФ і С₃ = 3 мкФ з’єднано, як показано на рис. 8.3, і під’єднано до джерела напруги U = 12 В. Визначити величину заряду на пластинах кожного конденсатора.

8.105. Визначити електроємність системи конденсаторів (рис. 8.4), якщо С₁ = 2 мкФ, а С₂= 1 мкФ.

Рис. 8.3 Рис. 8.4

8.106. Радіус внутрішньої сфери повітряного сферичного конденсатора R₁ = 1 см, радіус зовнішньої сфери R₂= 4 см. Між сферами прикладено різницю потенціалів U = 3 кВ. Яка напруженість електричного поля на відстані 3 см від центра сфер?

8.107. Радіус внутрішньої сфери повітряного сферичного конденсатора R₁= 1 см, радіус зовнішньої сфери R = 4 см. Між сферами прикладено різницю потенціалів U = 3 кВ. Яку швидкість отримає електрон, якщо він наблизиться до центра сфер з відстані r₁ = 3 см до r₂ = 2 см ?

8.108. Є дві концентричні металеві сфери з радіусами R₁ = 5 см і R₂ = 5,2 см, проміжок між якими заповнений парафіном. Внутрішній сфері надано заряд 10 мкКл. Визначити електроємність цієї системи і різницю потенціалів між сферами.

8.109. Радіус внутрішнього циліндра повітряного циліндричного конденсатора R₁ = 1,5 см, радіус зовнішнього циліндра R₂ = 3,5 см. Між циліндрами прикладено різницю потенціалів U = 2,3 кВ. Яку швидкість отримає електрон під дією поля цього конденсатора, рухаючись з відстані r₁ = 2,5 см до r₂ = 2 см від осі циліндра ? Яка напруженість електричного поля на відстанях r₁ і r₂ від осі циліндрів ?

8.110. Коаксіальний електричний кабель складається з центральної жили і концентричної відносно неї циліндричної оболонки, між якими міститься ізоляція. Визначити електроємність одиниці довжини такого кабелю, якщо радіус жили 1,5 см, радіус оболонки 3 см і діелектрична проникність ізоляції 3,2.

8.111. Між пластинами плоского конденсатора є діелектрик. Конденсатор заряджений до різниці потенціалів 1 кВ. Яка відносна діелектрична проникність діелектрика, якщо за його відсутності різниця потенціалів між обкладками конденсатора зростає до 3 кВ?

8.112. У двох однакових плоских конденсаторах простір між пластинами заповнено двома шарами однакової товщини з відносними діелектричними проникностямии ε₁ = 2 і ε₂= 6 В одному конденсаторі діелектричні шари розміщено паралельно до пластин, у другому – перпендикулярно (рис. 8.5). Визначити електроємність кожного конденсатора, якщо площа пластини 200 см², а відстань між пластинами 6 см. Рис.8.5

8.113. У простір між пластинами плоского повітряного конденсатора внесли плоскопаралельну металеву пластину товщиною d₁= 8 мм. Визначити електроємність конденсатора, якщо площа кожної пластини 100 см², а відстань між ними 10 мм.

8.114. Між пластинами плоского конденсатора, що розміщені на відстані 1 см одна від одної, прикладено різницю потенціалів 100 В. До однієї з пластин прилягає плоскопаралельна пластинка кристалічного бромистого талію (ε = 173) товщиною 9,5 мм. Після від’єднання конденсатора від джерела напруги пластинку кристала виймають. Яка буде після цього різниця потенціалів між пластинами конденсатора?

8.115. Між пластинами плоского конденсатора, що розміщені на відстані d = 1 см одна від одної, прикладено різницю потенціалів U = 300 В. У проміжку між пластинами розміщено плоскопаралельні пластинки скла товщиною d₁ = 0,5 см і парафіну товщиною d₂ = 0,5 см. Визначити: 1) напруженість електричного поля в кожній пластинці; 2) поверхневу густину заряду на пластинах.

8.116. Між пластинами плоского конденсатора розміщена скляна пластинка (ε = 7) товщиною 3 мм. Конденсатор заряджений до різниці потенціалів 1000 В. Визначити густину зв’язаних зарядів на поверхні скляної пластинки.

8.117. Між пластинами плоского конденсатора вносять тонку пластинку слюди (ε = 6). Якого тиску зазнає ця пластинка, якщо напруженість електричного поля 10 кВ/см ?

8.118. У горизонтально розташований повітряний плоский конденсатор з проміжком між пластинами d₁ = 7 см поклали на нижню пластину діелектрик товщиною d₂= 2 см з діелектричною проникністю ε = 6. Чому дорівнює напруженість електричного поля в центрі конденсатора, якщо різниця потенціалів на обкладках конденсатора U = 400 В ?

8.119. Куля, що занурена в гас, має поверхневу густину заряду σ = 11,3 мкКл/м² і потенціал φ = 4,5 кВ. Визначити радіус, заряд, ємність і енергію кулі.

8.120. Заряджену кулю А радіусом 2 см, привели в контакт з незарядженою кулею В, радіус якої 3 см. Після того як кулі роз’єднали, куля В мала енергію 0,4 Дж. Який був заряд на кулі А до їх зіткнення?

8.121. У плоский повітряний конденсатор з відстанню між обкладками d₁ = 6 см і площею кожної обкладки S = 200 см² внесено діелектричну пластинку товщиною d₂ = 3 см. Визначити зміну заряду на обкладках конденсатора, якщо діелектрична проникність матеріалу внесеної пластинки ε = 8, а конденсатор під’єднано до батареї з напругою U = 600 В.

8.122. У плоский повітряний конденсатор з відстанню між обкладками d₁ = 3 см і площею кожної обкладки S = 60 см² внесено металеву пластинку товщиною d₂ = 1 см. Визначити, яку енергію втратило джерело живлення при внесенні пластинки, якщо конденсатор під’єднаний до постійної напруги U = 2 кВ.

8.123. Плоский повітряний конденсатор складається з двох пластин, площа кожної S = 200 см², відстань між ними d₁= 0,3 см, Яку роботу потрібно виконати, щоб збільшити відстань між пластинами до d₂ = 0,5 см. Задачу розв’язати за умов: 1) конденсатор заряджають до U = 600 В і від’єднують від батареї; 2) конденсатор перебуває під постійною напругою U = 600 В.

8.124. Плоский конденсатор, площа кожної пластини якого S = 400 см², заповнений двома шарами діелектрика. Границя між ними паралельна до пластин. Перший шар – парафінований папір (ε₁ = 2) товщиною d₁ = 0,2 см, другий шар – скло (ε₂= 7 ) товщиною d₂= 0,3 см. Конденсатор заряджений до різниці потенціалів U = 600 В. Визначити енергію конденсатора.

8.125. Три конденсатори з електроємностями С₁ = 1 мкФ, С₂= 4 мкФ і С₃ = 10 мкФ з’єднано послідовно і під’єднано до джерела напруги. Визначити напругу джерела, якщо енергія другого конденсатора W₂= 2∙10^-3 Дж.

8.126. Два конденсатори з електроємностями С₁ = 4 мкФ, С₂= 3 мкФ зарядили зарядами q₁= 10^-4 Кл; q₂ = 10^-5 Кл і з’єднали паралельно. Визначити зміну енергії системи конденсаторів.

8.127. Батарею з двох послідовно з’єднаних конденсаторів, електроємності яких С₁ = 4 мкФ і С₂ = 6 мкФ, зарядили до різниці потенціалів 2 кВ і від’єднали від джерела напруги. На скільки зменшиться енергія батареї, якщо однойменно заряджені обкладки конденсатора з’єднати паралельно ?

8.128. Плоский конденсатор ємністю 60 пФ зарядили в повітрі до потенціалу 400 В. Після занурення конденсатора в рідкий діелектрик до половини висоти його пластин енергія конденсатора зменшилась на 1,2 мкДж. Визначити діелектричну проникність діелектрика.

8.129. Конденсатор електроємністю 600 пФ зарядили до різниці потенціалів 1,5 кВ і від’єднали від джерела напруги. Потім до нього приєднали незаряджений конденсатор ємністю 400 пФ. Визначити енергію, яка пішла на утворення іскри, при з’єднанні конденсаторів.

8.130. Визначити об’ємну густину енергії електричного поля зарядів в точці: 1) на відстані 2 см від поверхні зарядженої кулі радіусом 1 см; 2) поблизу великої зарядженої площини; 3) на відстані 2 см від довгого зарядженого провідника. Поверхнева густина заряду на кулі і площині дорівнює 16,7 мкК/м², а лінійна густина заряду на провіднику дорівнює 1,67·10 ⁷ Кл/м. Для всіх трьох випадків діелектрична проникність середовища дорівнює 2.

8.131. На заряд q₁ = 4,8∙10^-9 Кл, що міститься між обкладками плоского повітряного конденсатора електроємністю С = 17,8 пФ, діє сила F = 9,81∙10^-5 Н. Площа обкладки конденсатора S = 10^{-2 м2}. Визначити: 1) різницю потенціалів між обкладками; 2) заряд на обкладках конденсатора; 3 ) об’ємну густину енергії поля; 4) енергію електростатичного поля конденсатора.

8.132. Плоскопаралельну пластинку зі скла завтовшки 3 мм площею 400 см² помістили в однорідне електричне поле напруженістю 2 кВ/м, силові лінії якого перпендикулярні до поверхні пластинки. Визначити: 1) густину зв’язаних зарядів на поверхнях пластинки; 2) енергію електричного поля, зосереджену в пластинці; 3) енергію, накопичену в діелектрику при його поляризації; 4) енергію “незв’язаного” електричного поля в пластинці.

8.133. Відстань між обкладками плоского конденсатора d = 2∙10^{-3 м}, різниця потенціалів φ = 600 В. Заряд кожної обкладки q = 40 нКл. Визначити енергію електричного поля конденсатора і силу взаємного притягання обкладок.

8.134. Металеву кулю А радіусом R₁ = 10 см зарядили до потенціалу φ₁ = 2700 В і від’єднали від джерела напруги. Після цього кулю А з’єднали дротиною, ємністю якої можна знехтувати, з незарядженою металевою кулею В радіусом R₂ = 5 см. Визначити: 1) початковий заряд кулі А; 2) заряди куль після з’єднання; 3) потенціал куль після з’єднання; 4) енергію електричного поля обох куль після з’єднання; 5) енергію, що виділилася при з’єднанні.