Молекулярна фізика і термодинаміка

· Кількість речовини:

,

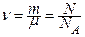де m – маса речовини; μ – молярна маса; N – кількість структурних елементів системи (молекул, атомів, іонів).

· Рівняння стану ідеального газу (рівняння Менделєєва-Клапейрона):

,

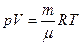де p – тиск газу; V –об’єм; T – температура газу у шкалі Кельвіна; 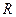– універсальна газова стала .

· Закон Дальтона:

,

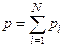де 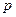– тиск суміші газів; 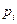– парціальний тиск i – го компонента газової суміші; 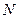– кількість компонентів.

· Основне рівняння молекулярно-кінетичної теорії газів:

,

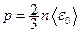де 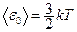– середня кінетична енергія поступального руху молекули; k – стала Больцмана; n – концентрація молекул.

· Залежність тиску газу від концентрації молекул і температури:

.

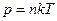· Розподіл молекул за швидкостями хаотичного теплового руху (розподіл Максвелла):

,

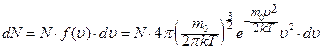де 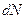– кількість молекул, швидкості яких лежать у інтервалі від υ до υ + dυ; N – загальна кількість молекул; f(υ) – функція розподілу молекул за швидкостями; 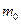– маса молекули газу.

· Розподіл частинок у полі потенціальних сил (розподіл Больцмана):

,

де 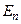– потенціальна енергія частинки; n та 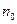–концентрації частинок в точках з потенціальними енергіями 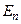та 0, відповідно.

· Барометрична формула:

,

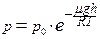де h – висота точки над рівнем, прийнятим за нульовий; p і p₀ - тиски повітря на висоті h і на нульовому рівні, відповідно; g – прискорення вільного падіння.

· Середня арифметична швидкість молекул:

.

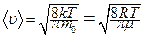· Середня квадратична швидкість:

.

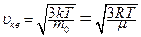· Найімовірніша швидкість молекул:

.

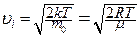· Середня довжина вільного пробігу молекул:

,

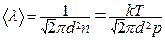де d – ефективний діаметр молекули.

· Середня кількість зіткнень, які зазнає молекула газу за одну секунду:

.

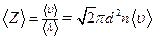· Маса речовини, що переноситься при дифузії:

,

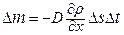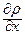де - коефіцієнт дифузії; - градієнт густини газу в напрямку осі 0Х; 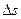- площа поверхні, перпендикулярної до осі 0Х; – час дифузії.

Для ідеального газу .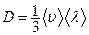

· Сила внутрішнього тертя у рідинах чи газах:

,

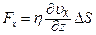де 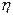- коефіцієнт в’язкості речовини; 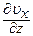- градієнт швидкості у напрямку перпендикулярному до напрямку руху шарів; 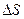– площа дотику шарів.

Для ідеального газу 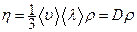, де 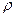- густина газу.

· Кількість теплоти, що переноситься внаслідок теплопровідності:

,

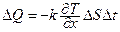де 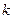- коефіцієнт теплопровідності речовини; 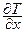- градієнт температури у напрямі, перпендикулярному до поверхні 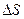, через яку переноситься тепло; 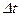– час перенесення.

Для ідеального газу 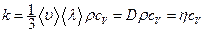, де 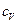- питома теплоємність газу при сталому об’ємі.

· Внутрішня енергія ідеального газу:

.

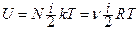де 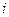- кількість ступенів вільності молекули; 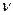- кількість молів газу.

· Перший закон термодинаміки:

,

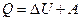де 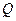– кількість теплоти, передана термодинамічній системі; 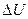– приріст внутрішньої енергії системи; 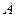– робота системи проти зовнішніх сил.

· Зв’язок між молярною і питомою теплоємностями:

,

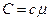де 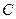– молярна теплоємність; 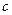– питома теплоємність.

· Молярна теплоємність при сталому об’ємі:

.

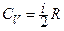· Молярна теплоємність при сталому тиску:

.

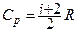· Рівняння Майєра:

.

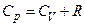· Робота ідеального газу при зміні його об’єму:

,

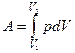де 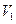та 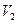- відповідно початковий та кінцевий об’єми газу.

· Робота при ізобарному процесі:

.

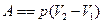· Робота при ізотермічному процесі:

.

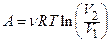· Рівняння адіабати:

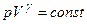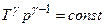, , або ,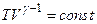

де 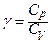- показник адіабати.

· Робота при адіабатному процесі:

, .

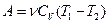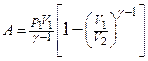· Рівняння політропи:

,

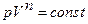де 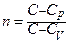- показник політропи; 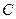- молярна теплоємність газу.

· Робота газу при політропному процесі:

.

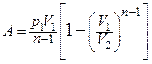· Коефіцієнт корисної дії прямого циклу теплової машини:

,

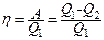де 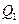- кількість теплоти, одержана робочим тілом від нагрівника; 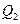- кількість теплоти, віддана робочим тілом холодильнику; 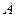- виконана робочим тілом робота.

· Коефіцієнт корисної дії теплової машини, яка працює за прямим циклом Карно:

.

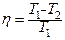де 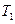– температура нагрівника; 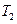– температура холодильника.

· Коефіцієнт корисної дії холодильної машини, яка працює за зворотним циклом:

,

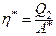де 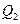- кількість теплоти, взятої робочим тілом від холодильника; 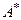– робота зовнішніх сил над робочим тілом.

· Для холодильної машини, яка працює за зворотним циклом Карно:

,

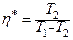де 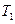- температура приймача тепла; а 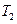- температура тіла, яке охолоджується.

· Зміна ентропії системи при переході зі стану 1 у стан 2:

.

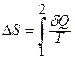Для ідеального газу .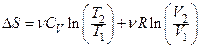

· Зв’язок між ентропією системи і термодинамічною ймовірністю її стану:

,

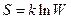де 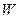- термодинамічна ймовірність стану системи.

· Рівняння стану реального газу:

.

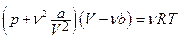де 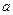і 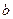- поправки Ван-дер-Ваальса для даного газу.

· Критичні параметри реального газу:

; ; ,

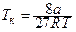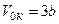де 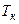– критична температура; 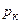– критичний тиск; 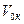– критичний об’єм одного моля.

· Внутрішня енергія реального газу:

,

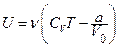де 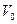- об'єм 1 моля газу.

· Рівняння Клапейрона-Клаузіуса:

,

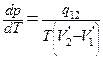де 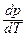- зміна тиску з температурою при фазовому переході, 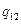- питома теплота фазового переходу, 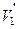і 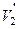- питомі об’єми першої та другої фаз.

· Закон Дюлонга і Пті:

,

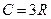де 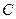- молярна теплоємність хімічно простого кристалічного твердого тіла.

· Коефіцієнт поверхневого натягу рідини:

,

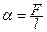де 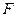- сила поверхневого натягу; 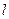– довжина контура, що обмежує поверхню рідини.

· Зміна вільної енергії поверхні плівки рідини при зміні її площі:

,

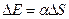де 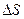– зміна площі поверхні рідини.

· Додатковий тиск, викликаний кривиною поверхні рідини:

,

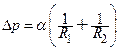де 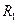і 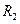- радіуси кривини двох взаємно-перпендикулярних перерізів поверхні рідини.

· Висота підіймання (опускання) рідини у капілярній трубці:

,

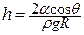де 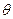- крайовий кут, 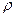- густина рідини, 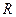- радіус капіляра.

7.1. Визначити кількість речовини та кількість молекул в 1 кг молекулярного азоту.

7.2. Скільки молів речовини і скільки атомів міститься у 2 л ртуті ?

7.3. Знайти масу атома магнію.

7.4. Визначити концентрацію атомів у рідкій ртуті та об’єм, який припадає на один атом.

7.5. Визначити об’єм, який припадає на пару іонів 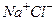в кристалі хлористого натрію. Густина кристалу – 2165 кг/м³.

7.6. Який об’єм припадає на один атом у кристалі міді? Густина міді – 8600 кг/м³.

7.7. Налита у склянку вода масою 0,18 кг повністю випарувалася за 20 діб. Скільки молекул випаровувалося з поверхні води за 1 с ?

7.8. Скільки частинок міститься в 1·10^{-2 кг} пари брому, якщо ступінь дисоціації молекул 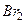дорівнює 25 % ?

7.9. Визначити густину аргону в балоні при тиску за манометром (надлишковому над атмосферним) 9900 кПа і температурі 320 К. Скільки атомів газу міститься при цьому в 1 см³ ? Атмосферний тиск 100 кПа.

7.10. Тиск залишкових газів у радіолампі 1·10^-5 Па при температурі 300 К, об’єм колби 5·10^-6 м³. Визначити концентрацію молекул у лампі, їх загальну кількість, а також густину газу, вважаючи, що його молярна маса дорівнює 29 кг/кмоль.

7.11. Тиск водяної пари при 17 °С становить1000 Па. Визначити густину пари і концентрацію молекул в ній.

7.12. Сучасні методи створення вакууму дозволяють досягти тиску повітря 1,33·І0^-9 Па. Визначити густину і концентрацію молекул повітря при такому тиску та температурі 300 К, якщо молярна маса повітря дорівнює 29 кг/кмоль.

7.13. Для отримання високого і надвисокого вакууму всі вузли вакуумної системи прогрівають, щоб зняти з їх поверхні адсорбовані молекули газу. Розрахувати тиск молекул газу, десорбованих з поверхні стінок у камері мас-спектрометра в процесі нагрівання камери до 250 °С, якщо камера має форму циліндра довжиною 0,50 м і діаметром 0,05 м. Вважати, що стінки покриті одномолекулярним шаром молекул газу і на одну молекулу припадає площа 1·10^{-19 м2}.

7.14. У посудині при температурі 17 °С міститься суміш 10 г водню та 14 г азоту під тиском 200 кПа. Визначити об'єм посудини та густину суміші.

7.15. При нагріванні двоатомного газу в герметично запаяній ампулі від Т₁ = 300 К до Т₂ = 800 К його тиск зростає від 150 кПа до 500 кПа. Припускаючи, що при температурі Т₁ дисоціація молекул газу відсутня, визначити ступінь дисоціації газу при температурі Т₂.

7.16. У герметично запаяній кварцовій ампулі об’ємом 100·10^{-6 м3} міститься 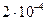кг йоду при температурі 1000 °С і тиску 90 кПа. Визначити ступінь дисоціації молекул йоду.

7.17. Шлюзова камера електронного мікроскопа має об’єм 30 см³. Яким повинен бути об’єм допоміжного балона з тиском 1 Па, щоб після з’єднання шлюзової камери з балоном тиск не перевищив 13 Па, що дозволить ввести зразок в колону мікроскопа через шлюз без напускання в колону повітря при атмосферному тиску 100 кПа і температурі 300 К. Процес вважати ізотермічним.

7.18. Після одного робочого ходу поршня вакуумного насоса тиск у вакуумній установці знизився від 101 кПа до 100 кПа. Яким буде тиск після 85 робочих ходів поршня? Температуру газу вважати сталою.

7.19. Скільки робочих ходів повинен виконати поршень вакуумного насоса, щоб зменшити тиск повітря у вакуумній камері об’ємом 20·10^{-3 м3} від атмосферного 1,00·10⁵ Па до 10 Па, якщо робочий об’єм циліндра 100·10^{-6 м3}? За скільки часу буде зменшено тиск, якщо поршень виконує 5 робочих ходів за секунду? Температуру повітря в камері в процесі зменшення тиску вважати сталою.

7.20. Два балони об’ємами 60·10^{-3 м3} та 20·10^{-3 м3} заповнені киснем до тиску 10·10⁶ Па та 0,5·10⁵ Па відповідно (вказано значення тиску, надлишкове над атмосферним). Який тиск покаже манометр при з’єднанні цих балонів тонкою трубкою? Яка маса кисню перейде з першого балона в другий? Температура газу становить 300 К і не змінюється після з’єднання балонів.

7.21. Повітряну кулю наповнюють гарячим повітрям при температурі 330 К. Температура зовнішнього повітря 290 К. Яким повинен бути мінімальний об^’єм кулі, щоб вона могла відірватися від Землі, якщо маса оболонки і вантажу 300 кг? Атмосферний тиск 100 кПа.

7.22. Яку найбільшу масу вантажу може втримати в завислому стані метеозонд об^’ємом 20 м³, заповнений воднем, коли температура повітря та водню 230 К, маса оболонки 13 кг ? Тиск в метеозонді дорівнює атмосферному 100 кПа. Молярна маса повітря 29 кг/кмоль.

7.23. Компресор засмоктує повітря при атмосферному тиску 100 кПа і подає в балон об’ємом 10·10^{-3 м3}. Скільки робочих ходів повинен здійснити поршень компресора, щоб після охолодження газу до початкової температури тиск у балоні став 20·10⁵ Па ? За один хід поршня всмоктується об’єм повітря 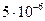м³. Атмосферний тиск 100 кПа. Початковий тиск повітря у балоні дорівнює атмосферному. Об^’ємом з’єднувальних трубок знехтувати.

7.24. Манометр на балоні з киснем показує тиск 900 кПа. Визначити масу кисню в балоні, якщо об’єм балона 25·10^{-3 м3} і температура 300 К. Атмосферний тиск 100 кПа.

7.25. Визначити масу газу в м’ячі, якщо його діаметр 0,20 м, а після того, як нанього став футболіст масою 70 кг, на плоскій поверхні ґрунту залишився слід від м’яча діаметром 0,15 м. Температура повітря 300 К, атмосферний тиск 100 кПа, оболонку вважати тонкою. Пружністю оболонки та зміною її об’єму при навантаженні знехтувати.

7.26. У скільки разів кількість молекул, швидкості яких лежать в інтервалі 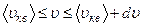, менша від кількості молекул з швидкостями в інтервалі 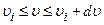при однакових температурах?

7.27. У скільки разів кількість молекул із швидкостями, значення яких лежать в інтервалі 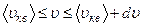,меншавід кількості молекул з швидкостями в інтервалі ?

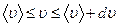7.28. У скільки разів більша кількість молекул із швидкостями в інтервалі 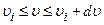від кількості молекул, швидкості яких лежать в інтервалі?

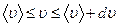7.29. Середня квадратична швидкість молекул деякого газу дорівнює 450 м/с. Тиск газу 5·10⁴ Па. Визначити густину газу за цих умов.

7.30. При якій температурі середня квадратична швидкість молекули азоту дорівнює другій космічній швидкості для Землі (11,2 км/с)?

7.31. Який відсоток молекул газу має швидкість, що відрізняється від найімовірної швидкості не більше, ніж на 1 %?

7.32. Визначити відносну кількість молекул ідеального газу, кінетичні енергії яких відрізняються від найімовірнішого значення енергії не більше, ніж на 1 %.

7.33. Визначити температуру гелію, для якої середня квадратична швидкість атомів гелію більша за середню арифметичну швидкість на 200 м/с.

7.34. При якій температурі функція розподілу молекул кисню за швидкостями має максимум при швидкості 500 м/с?

7.35. Для якого газу при температурі 295,6 К різниця між середньою арифметичною та найімовірнішою швидкостями руху молекул дорівнює 45,0 м/с?

7.36. При якій температурі молекулярного кисню ймовірності знаходження молекул з швидкостями в інтервалах від 200 м/с до 201 м/с та від 500 м/с до 501 м/с однакові?

7.37. При якій температурі функція розподілу Максвелла для молекулярного водню має втричі більше значення для швидкості 500 м/с, ніж для 1500 м/с?

7.38. Найвища гора українських Карпат - гора Говерла - має висоту 2061 м над рівнем моря. Визначити тиск повітря на вершині гори, якщо атмосферний тиск на рівні моря 101 кПа, а температура 270 К. Вважати, що температура повітря не змінюється з висотою.

7.39. Визначити різницю атмосферних тисків на Ужокському (889м над рівнем моря)та Воловецькому (1014 м над рівнем моря) перевалах Карпат, вважаючи, що температура повітря є сталою і дорівнює 290 К.

7.40. Визначити, у скільки разів густина повітря на карпатській горі Парашці (висота 1262 м над рівнем моря) менша, ніж на рівні моря. Температура повітря 290 К стала у всьому діапазоні висот.

7.41. Біля поверхні Землі відношення концентрацій молекул кисню і азоту в повітрі становить 0,27. Вважаючи, що температура повітря не змінюється з висотою і дорівнює 273 К, обчислити відношення цих концентрацій на висоті 8848 м (гора Еверест).

7.42. Вважаючи, що температура повітря (280 К) і прискорення вільного падіння (9,8 м/с²) однакові на різних висотах, визначити, в скільки разів відношення концентрацій молекул водню і азоту біля поверхні Землі відрізняється від їх відношення на висоті 2000 м.

7.43. Покази альтиметра літака мають систематичну похибку, завищуючи тиск повітря на 800 Па. На скільки буде відрізнятись показ висотоміра від реального значення на висоті 5000 м? Атмосферний тиск на поверхні Землі 100 кПа. Температуру повітря (270 К) і прискорення вільного падіння (9,8 м/с²) вважати однаковими на різних висотах.

7.44. На якій висоті від підніжжя гори перебуває група альпіністів, якщо наявний у неї барометр показує тиск 73 кПа, а барометр у рятувальної служби біля підніжжя гори показує тиск 91 кПа? Температура повітря 280 К.

7.45. Визначити силу, яка діє на частинку в однорідному полі сил тяжіння, якщо відношення концентрацій частинок на двох рівнях, віддалених один від одного вздовж вертикалі на 1 м, дорівнює 2,71. Температура системи 300 К.

7.46. Оцінити середню температуру атмосфери Землі, знаючи, що на висоті 230 км густина повітря дорівнює 10^-10 кг/м³. Вважати температуру атмосфери сталою, прискорення вільного падіння 9,5 м/с², молярну масу повітря 29 кг/кмоль.

7.47. Припустивши, що молекули рухаються у всіх можливих напрямках з швидкостями 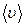, які не залежать від напрямку руху, визначити середнє значення відносної швидкості молекул.

7.48. Вивести формулу для обчислення середньої довжини вільного пробігу молекул газу через його тиск і температуру.

7.49. Визначити середню довжину вільного пробігу і середній час між зіткненнями молекул газоподібного азоту при 273 К: 1) при нормальному атмосферному тиску (101 кПа); 2) при граничному розрідженні, що досягається магніторозрядним насосом (1,3·10^-9 Па).

7.50. Середнім вакуумом називають стан газу, при якому довжина вільного пробігу молекул газу близька до лінійних розмірів посудини. Визначити, який тиск повітря відповідає визначенню середнього вакууму для вакуумного напилювального поста ВУП-2К, діаметр робочої камери якого 0,30 м. Ефективний діаметр молекул повітря – 3,74·10^{-10 м}, температура – 300 К.

7.51. Повітря заповнює пору в сорбенті діаметром 0,05 мкм. При якому тиску впорі буде середній вакуум ? Параметри повітря взяти з попередньої задачі.

7.52. Магніторозрядний насос працює в області тисків від 13 Па до 6,6·10^-7 Па. Обчислити концентрації та довжини вільного пробігу молекул на початку та в кінці робочого тиску, якщо температура повітря 300 К.

7.53. Вакуум, при якому газ має тиск, менший, ніж 10^-5 Па, називають надвисоким. Обчислити густину водню при такому тиску, концентрацію його молекул та середню довжину їх вільного пробігу. Ефективний діаметр молекули водню 2,75·10^{-10 м}, температура 400 К.

7.54. Скільки зіткнень зазнає молекула кисню (ефективний діаметр 3,64·10^{-10 м})протягом 100 с при тиску 100 Па і температурі 400 К?

7.55. Визначити кількість всіх зіткнень, які відбуваються протягом 1 с між всіма молекулами водню, що займає за нормальних умов об’єм 1 мм³.

7.56. Скільки зіткнень за секунду зазнає молекула неону при температурі 600 К і тиску 133 Па? Ефективний діаметр молекули неону становить 2,04І0^{-10 м}.

7.57. У колбі об’ємом 1·10^{-4 м3} міститься 10^{-4 кг} азоту. Визначити середню довжину вільного пробігу молекул азоту за цих умов.

7.58. Гелій перебуває під тиском 100 кПа при температурі 300 К. Діаметр атома гелію 2·10^{-10 м}. У скільки разів середня довжина вільного пробігу атомів гелію перевищує середню відстань між його атомами? Прийняти, що середня відстань між атомами газу дорівнює кореневі кубічному із об’єму, який припадає на один атом газу.

7.59. Як залежить середня довжина вільного пробігу та концентрація молекул газу від температури при ізохорному процесі?

7.60. Як залежить середня довжина вільного пробігу та кількість зіткнень молекули за одиницю часу від температури при ізобарному процесі?

7.61. Термопарна манометрична лампа ПМТ-2 забезпечує вимірювання тиску повітря в діапазоні від 67 до 0,13 Па. Визначити значення середньої довжини вільного пробігу молекул газу при цих тисках і порівняти його з діаметром лампи (30 мм). Яким рівням вакууму (низькому, середньому, високому) відповідають ці тиски? Ефективний діаметр молекули повітря 3,74·І0^{-10 м}. Температура повітря в лампі 370 К.

7.62. Визначити питому теплоємність водяної пари при сталому тиску і при сталому об’ємі. Визначити їх відношення .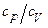

7.63. Визначити питому теплоємність азоту 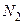при сталому тиску і при сталому об’ємі. Визначити їх відношення .

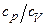7.64. Визначити питому теплоємність пари ртуті при сталому тиску і при сталому об’ємі. Визначити їх відношення .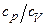

7.65. Визначити питому теплоємність при сталому тиску та сталому об’ємі для окису азоту 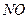. Визначити їх відношення .

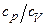7.66. Визначити молярну теплоємність гелію при сталому тиску і при сталому об’ємі.

7.67. Визначити молярну теплоємність кисню при сталому тиску і при сталому об’ємі.

7.68. Обчислити внутрішню енергію 14 г азоту при 300 К.

7.69. Обчислити внутрішню енергію 30 г аргону при 273 К.

7.70. Визначити молярну масу одноатомного газу, питома теплоємність якого при сталому об^’ємі 311,8 Дж/кг·К. Вказати назву хімічного елемента.

7.71. Для якого двоатомного газу питома теплоємність при сталому об^’ємі 10393 Дж/кг·К. Вказати його хімічну формулу.

7.72. Визначити питому теплоємність неону при сталому тиску. Молярна маса неону 20 кг/кмоль.

7.73. Визначити питому теплоємність ненасиченої водяної пари при сталому тиску.

7.74. Визначити питомі теплоємності ідеального газу при сталому тиску та сталому об^’ємі, якщо 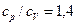, а молярна маса 28 кг/кмоль.

7.75. Визначити, яка ступінь дисоціації молекул кисню, коли питома теплоємність при сталому тиску дорівнює 1050 Дж/кг·К.

7.76. Визначити питомі теплоємност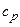і і 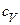водню, коли ступінь дисоціації його молекул на атоми дорівнює 25%.

7.77. Визначити ступінь дисоціації пари брому, коли 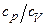= 1,476.

7.78. Визначити питому теплоємність при сталому тиску суміші газів, що містить 2 моля неону та 10 молів гелію.

7.79. Визначити відношення 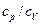для суміші 1 моля гелію та 0,5 моля кисню.

7.80. При ізохорному процесі газ отримав 831 Дж тепла. На скільки зросла його внутрішня енергія ? Яку роботу виконав газ ?

7.81. При ізотермічному процесі газ отримав 314 Дж тепла. Обчислити зміну внутрішньої енергії газу та виконану ним роботу.

7.82. 20 г аргону ізотермічно розширюються при температурі 27 °С і виконують роботу 1000 Дж. У скільки разів змінився тиск газу при розширенні?

7.83. При ізобарному нагріванні 40 г аргону виконана робота 50 Дж. Скільки тепла отримав газ і на скільки зросла його внутрішня енергія?

7.84. Газ отримав 500 Дж тепла і виконав при цьому роботу 273 Дж. Визначити зміну внутрішньої енергії газу.

7.85. Газ, адіабатно розширюючись, виконав роботу 100 Дж. На скільки змінилася його внутрішня енергія?

7.86. Суміш гелію та неону масою 100 г займає об^’єм 32,41 л. Манометр показує (надлишковий над атмосферним) тиск 900 кПа. Визначити процентний вміст за масою обидвох газів у суміші, якщо температура суміші 300К, атмосферний тиск 100 кПа.

7.87. Питома теплоємність суміші гелію та неону при сталому об’ємі 1246,5 Дж/кг К. Визначити відношення маси неону до маси гелію в суміші.

7.88. Скільки тепла потрібно надати 56 г азоту, щоб нагріти його при сталому тиску на 50 К? Яку роботу виконає газ при розширенні?

7.89. Аргон нагрівають при сталому тиску, надаючи йому 425 Дж тепла. Яку роботу виконає газ?

7.90. Азот нагрівають при сталому тиску. Скільки тепла отримав газ, якщо при розширенні ним виконана робота 168 Дж?

7.91. Вуглекислий газ нагріли при сталому тиску. На скільки зросла його внутрішня енергія, якщо газ отримав 224 Дж тепла?

7.92. Для нагрівання 8 г гелію від 36 до 56 °С затрачено 831,4 Дж тепла. Як проводили нагрівання: при сталому об^’ємі чи сталому тиску?

7.93. У балоні об^’ємом 5 л міститься аргон під тиском 200 кПа. У скільки разів збільшиться тиск у балоні, якщо газ отримає 450 Дж тепла? Початкова температура 300 К.

7.94. Виходячи із рівняння Пуассона 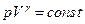і рівняння стану ідеального газу Клапейрона-Менделєєва, виразити рівняння адіабати через змінні 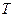та .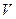

7.95. Виразити рівняння адіабати через змінні 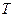та .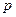

7.96. Користуючись рівнянням Пуассона і формулою для розрахунку роботи при зміні об^’єму газу, встановити формулу для обчислення роботи газу при адіабатному процесі за відомим початковим станом ( 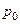, 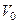) та кінцевим об’ємом газу.

7.97. Вивести формулу для розрахунку роботи газу при адіабатному процесі за відомими початковим станом і кінцевою температурою газу.

7.98. Із аналізу рівняння стану ідеального газу при політропному процесі 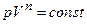визначити значення показника політропи 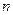та теплоємність газу 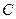при ізобарному процесі.

7.99. Встановити, яке значення показника політропи відповідає ізотермічному процесу та теплоємність газу у цьому випадку. Примітка: проаналізуйте рівняння ізотерми.

7.100. Визначити значення показника політропи, який відповідає ізохорному процесові.

7.101. Визначити показник політропи та теплоємність ідеального газу при адіабатному процесі.

7.102. Об^’єм гелію при адіабатному розширенні зріс у 2рази. Визначити температуру гелію після розширення і виконану ним роботу, якщо його початковий стан: об’єм – 2,0 л, температура – 300 К, тиск – 1,00 МПа.

7.103. Аргон масою 400 г, що був при температурі 300 К та тиску 1,00·10⁵ Па, адіабатно стискають до тиску 1,00·10⁷ Па. Визначити температуру газу в кінці стиску, відношення початкового об’єму до кінцевого і виконану газом роботу.

7.104. Визначити показник політропи для одноатомного ідеального газу, який в ході процесу має сталу молярну теплоємність .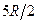

7.105. Визначити показник політропи для процесу, в ході якого двоатомний ідеальний газ має сталу молярну теплоємність 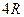. Вважати, що коливальні рухи молекул при температурі протікання процесу не збуджуються.

7.106. Визначити показник політропи для процесу, в ході якого 3- атомний ідеальний газ має сталу молярну теплоємність 3,25 R. Коливальними рухами молекул при температурі процесу знехтувати.

7.107. Обчислити значення показника політропи 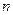для процесу, в якому .

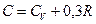7.108. Виразити молярну теплоємність С ідеального газу при політропному процесі через показник політропи 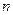та показник адіабати .

7.109. Вияснити, при яких значеннях показника політропи теплоємність ідеального газу: а) додатна; б) від’ємна; в) безмежно велика; г) дорівнює нулю.

7.110. Визначити молярну теплоємність (в одиницях, що дорівнюють 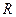)ідеального двоатомного газу для процесу із показником політропи n = 0,9 та 1,1.

7.111. Ідеальний газ розширюється політропно. При яких значеннях показника політропи температура газу буде: а) зростати; б) зменшуватись; в)залишатися незмінною?

7.112. Ідеальний газ розширюється так, що його тиск зростає пропорційно до об’єму. Встановити, чи є даний процес політропним, і якщо так - визначити молярну теплоємність газу.

7.113. Ідеальний газ розширюється за законом 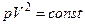. Встановити: а) чи процес розширення політропний; б) молярну теплоємність газу в такому процесі; в) нагрівається чи охолоджується газ при розширенні?

7.114. Визначити роботу, виконану 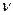молями газу при політропному процесі з молярною теплоємністю 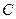через температури початкового 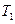і кінцевого 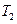станів газу. Яку кількість тепла 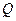при цьому отримує газ?

7.115. Одноатомний газ політропно стиснули від 4,0 л до 2,0 л. При цьому тиск зріс від 100 кПа до 500 кПа. Визначити молярну теплоємність газу при такому процесі.

7.116. Яку роботу виконали 7молів одноатомного газу при адіабатному розширенні від об’єму 1,0 л до 5,0 л ? Початковий тиск газу 1,0 МПа.

7.117. Двоатомний газ адіабатно розширюється від 1 л до 5 л. Початкова температура газу 300 К. Яка температура газу після розширення?

7.118. 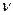молів гелію політропно нагріли від температури 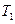до 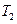. Скільки тепла отримав газ, якщо показник політропи ?

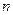7.119. Визначити роботу, виконану 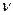молями ідеального газу, який зі стану із тиском 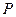, об’ємом 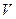і температурою 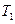розширився адіабатно і охолонув до температури ?

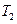7.120. Повітря в циліндрі дизельного двигуна автомобіля стискається у 17разів. Обчислити температуру повітря перед вприскуванням палива, якщо початкова температура 300 К. Яка робота виконана при стиску повітря? 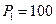кПа, V₁= 2,0 л. Повітря вважати двоатомним газом із жорсткими молекулами.

7.121. Обчислити коефіцієнт дифузії водню при тиску 100 кПа і температурі 300 К. Ефективний діаметр молекули водню 2,3·10^{-10 м}.

7.122. Обчислити коефіцієнт дифузії гелію та довжину вільного пробігу його атомів при температурі 400 К і тиску 100 кПа. Ефективний діаметр атома гелію 2,0·10^{-10 м}.

7.123. Визначити відношення коефіцієнтів самодифузії водню та азоту при однакових тисках і температурах. Ефективний діаметр молекули водню 2,3·10^{-10 м}, азоту - 3,0·10^{-10 м}.

7.124. Визначити масу азоту, що продифундує крізь пластину площею 0,100 м² за 10 с, якщо градієнт густини азоту в перпендикулярному до неї напрямку 1 кг/м⁴ , температура 300 К, середня довжина вільного пробігу молекул азоту 1·10^{-7 м}.

7.125. Визначити масу водню, що продифундує за 1 с крізь пластину площею 10^{-4 м2}, якщо концентрації молекул на поверхнях пластини - постійні і дорівнюють, відповідно, 4·10¹⁸ та 2·10¹⁵ м^-3, товщина пластини 2,0 мм, коефіцієнт дифузії 2,15·10^-8 м²/с.

7.126. Коефіцієнт дифузії азоту при тиску 100 кПа і температурі 300 К дорівнює 1,42·10^-5 м²/с. Обчислити довжину вільного пробігу та ефективний діаметр молекули азоту за даних умов.

7.127. В результаті деякого процесу в’язкість ідеального газу зросла в 3 рази, коефіцієнт дифузії - в 6разів, а температура у 1,2раза. У скільки разів змінився тиск газу?

7.128. Як зміняться довжина вільного пробігу молекул, коефіцієнт дифузії, коефіцієнт в’язкості та коефіцієнт теплопровідності ідеального двоатомного газу, якщо його об’єм ізотермічно збільшиться у 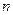разів?

7.129. Відпущена у рідині сталева кулька радіусом 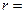2·10^{-3 м} рівномірно опускається із швидкістю 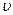=0,2 мм/с. Визначити коефіцієнт в’язкості рідини, якщо густина рідини дорівнює 1,2·10³ кг/м³.

7.130. Визначити коефіцієнти дифузії і внутрішнього тертя азоту за нормальних умов. Ефективний діаметр молекули азоту дорівнює 3,1·10^-10 м.

7.131. На вертикальній ділянці шляху довжиною 1,500 ± 0,005 м сталева кулька діаметром 3,00±0,01 мм рухається в гліцерині вниз із сталою швидкістю протягом 65,5 ± с. Визначити коефіцієнт в’язкості гліцерину та обчислити відносну похибку результату вимірювання.

7.132. Яку найбільшу швидкість може розвинути крапля дощу діаметром 0,3 мм, якщо температура повітря 20 °С, атмосферний тиск 100 кПа, ефективний діаметр молекул повітря 0,3 нм, молярна маса повітря 0,029 кг/моль ?

7.133. У скільки разів теплопровідність молекулярного водню за нормальних умов більша, ніж молекулярного азоту , якщо довжина вільного пробігу молекул за даних умов дорівнює 15,82·10^{-8 м} для водню та 9,30·10^{-8 м} для азоту ?

7.134. Визначити коефіцієнт теплопровідності повітря при тиску 10⁵ Па і температурі 300 К, вважаючи, що ефективний діаметр молекул повітря 3,5·10^{-10 м}. Молярна маса повітря 29 кг/кмоль.

7.135. Простір між великими паралельними горизонтальними пластинамизаповнений азотом. Відстань між пластинами 40 мм, температура пластин стала і дорівнює 300 К у нижньої та 400 К - у верхньої. Тиск газу 100 кПа, ефективний діаметр молекул 3,7·10^{-10 м}, молярна маса азоту 28 кг/кмоль. Визначити густину потоку тепла, що переноситься азотом між пластинами. При обчисленні коефіцієнта теплопровідності використати середнє значення температури .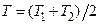

7.136. Визначити густину потоку тепла, який переносить азот при тиску 1,0 Па між двома паралельними пластинами з температурами 300 та 350К, розташованими на відстані 5,0 мм одна від одної. При обчисленні коефіцієнта теплопровідності використайте середнє значення температури .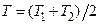

7.137. Відстань між стінками колби термоса 10 мм. Починаючи з якого значення тиску повітря між стінками теплопровідність його почне зменшуватись при відкачуванні? Температура повітря 290 К, діаметр молекули 3.5·10^-10 м.

7.138. Обчислити величину густини теплового потоку 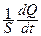, який виникає між двома паралельними пластинами, розташованими на відстані 2 см, завдяки теплопровідності азоту, що заповнює простір між пластинами, для тисків 1,00·10⁵ Па, 1,00·І0⁴ Па, 1,00 Па, 0,10 Па та 0,010 Па. Температури пластин 295 К та 305 К.

7.139. Для розрахунку опалювальної системи треба розрахувати втрати тепла крізь 1 м² стіни приміщення протягом доби. Товщина стіни 50 см, температура стіни ззовні і зсередини приміщення відповідно дорівнює 243 К та 291 К, коефіцієнт теплопровідності 0,20 Вт/м×К.

7.140. Антикатод рентгенівської трубки виконаний у вигляді мідного стержня довжиною 50 мм і діаметром 15 мм. Визначити перепад температур між гарячим і холодним кінцями стержня, нехтуючи втратами тепла через його бокову (циліндричну) поверхню. Холодний кінець охолоджується проточною водою, яка нагрівається на 3 К при витраті 1 кг/хв.

7.141. В якому випадку к.к.д. циклу Карно зросте більше: при підвищенні температури нагрівника на деяку величину при незмінному значенні температури холодильника, чи при зниженні на таку ж величину температури холодильника при незмінному значенні температури нагрівника?

7.142. Ідеальний газ виконує цикл Карно. Температура нагрівника в 3 рази вища від температури холодильника. Яка частина теплоти, одержаної за один цикл від нагрівника, перетворюється в механічну роботу?

7.143. Ідеальна теплова машина працює за циклом Карно. Температура нагрівника 550 К, холодильника – 300К. Протягом циклу робоче тіло одержало від нагрівника 8,20·10⁴ Дж теплоти. Визначити: 1) к.к.д. машини; 2) корисну роботу, виконану за один цикл; 3) кількість теплоти, яка віддається за один цикл холодильнику.

7.144. Газ, який виконує цикл Карно, одержує від нагрівника 25,0 кДж теплоти. Яка температура нагрівника, якщо за цикл виконується робота 10,0 кДж при температурі холодильника 300 К?

7.145. Протягом одного циклу Карно газ виконує роботу 42,0 кДж, віддаючи при цьому холодильнику 21,0 кДж теплоти. У скільки разів температура нагрівника вища від температури холодильника ?

7.146. Найбільший тиск газу, що виконує цикл Карно, становить 1,20 МПа, тиск в кінці ізотермічного розширення - 550 кПа, а в кінці ізотермічного стиску - 350 кПа. Який найменший тиск газу протягом цього циклу?

7.147. Один моль азоту виконує прямий цикл Карно, причому відношення максимального за цикл об’єму до мінімального становить 10. Температура нагрівника 580 К, холодильника - 290 К. Визначити: 1) кількість теплоти, одержаної газом за цикл; 2) роботу, виконану за цикл; 3) к.к.д. циклу.

7.148. 1 кг кисню виконує цикл Карно в інтервалі температур від 300 К до 600 К. Тиск газу в кінці ізотермічного розширення дорівнює тиску на початку адіабатного стиску. Визначити потужність установки, якщо цикл триває 0,500 с.

7.149. Ідеальний газ виконує цикл, що складається з ізобари, ізохори та ізотерми (рис. 7.1), причому в стані 1 газ займає об’єм 2,00 л при тиску 500 кПа, а в стані 2 - об’єм 4,00 л. Визначити роботу газу за цикл. Рис.7.1.

/?_.'!

7.150. Прямий цикл, що складається з двох ізохор та двох ізобар, виконуєтьсядвоатомним ідеальним газом, причому об’єм газу змінюється від 5,00 л до 10,0 л, а тиск – від 200 до 400 кПа. Побудувати графік циклу та визначити його к.к.д.

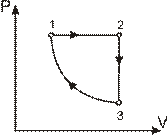
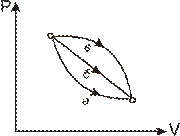
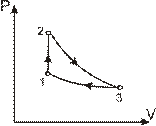7.151. На рис. 7.2. показаний цикл, який виконує ідеальний газ. (2 -3 - адіабата, 3-1 – ізотерма). Найнижча температура протягом циклу становить 200 К, найвища – 520 К. Визначити к.к.д. циклу.

Рис. 7.2

7.152. У карбюраторному двигуні внутрішнього згоряння двоатомний ідеальний газ виконує цикл, що складається з двох ізохор і двох адіабат (рис. 7.3.). Визначити відношення об’ємів у станах 1 і 2 (ступінь стиску), якщо к.к.д. циклу 0,575. Рис. 7.3

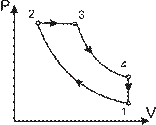7.153. Яку потужність розвиває двигун внутрішнього згоряння, що працює за циклом, зображеним на рис.7.3, якщо в двигуні за 1 год згоряє 5,7 кг палива? Вважати, що робочим тілом в двигуні є багатоатомний ідеальний газ, ступінь адіабатного стиску якого 8,5. Питома теплота згоряння палива 4,6·10⁷ Дж/кг.

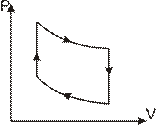7.154. Двигун внутрішнього згоряння працює за циклом Дизеля (рис. 7.4). Процеси 1-2 і 3-4 - адіабатні. Визначити Рис. 7.4 к.к.д. циклу, якщо об’єм двоатомного ідеального газу в станах 1, 2 і 3 становить відповідно 1,30 л, 0,018 л і 0,520 л.

7.155. Ідеальний одноатомний газ виконує цикл, що складається з двох ізохор і двох ізотерм (рис. 7.5). Температура газу змінюється за цикл від 290 К до 500 К, а відношення максимального і мінімального об’ємів становить 4. У скільки разів к.к.д. цього циклу менший від к.к.д. циклу Карно, який виконується в тому ж інтервалі температур? Рис. 7.5

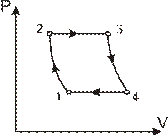7.156. 1 г азоту виконує цикл, що складається з двох ізобар і двох адіабат (рис. 7.6). Мінімальний та максимальний об’єми газу становлять відповідно 1,00 л і 3,00 л, а мінімальний та максимальний тиски - 100 кПа і 200 кПа. Визначити: 1) температури газу в станах 1, 2, 3 та 4; 2) роботу, виконану за цикл; 3) к.к.д. циклу.

Рис. 7.6

7.157. Визначити температуру в камері холодильника, якщо кількість теплоти, відведеної з камери за деякий проміжок часу, в 6 разів перевищує роботу, виконану двигуном за той же час. Температура навколишнього повітря 290 К. Вважати, що холодильник працює за зворотним циклом Карно.

7.158. Ідеальна холодильна машина працює за зворотним циклом Карно. Зовнішні сили виконують за цикл роботу 2,10 кДж. Температура тіла, яке охолоджують, 280 К, температура теплоприймача 350 К. Яка кількість теплоти відбирається від охолоджуваного тіла за один цикл? Передається теплоприймачу за один цикл? Який холодильний коефіцієнт машини?

7.159. Холодильний коефіцієнт машини, яка виконує зворотний цикл Карно, дорівнює 3. Який к.к.д. теплової машини, що виконує той же цикл в прямому напрямі?

7.160. 2 молі азоту виконують зворотний цикл Карно в інтервалі температур від 270 К до 290 К. Максимальний об’єм газу за цикл в 4рази більший від мінімального. Визначити роботу зовнішніх сил за цикл і холодильний коефіцієнт холодильної машини.

7.161. Ідеальна машина, яка працює за зворотним циклом Карно, забирає теплоту від води, що має температуру 273 К, і передає її кип’ятильнику з водою при температурі 373 К. Яка маса води замерзне в резервуарі, що охолоджується, якщо в кип’ятильнику перетвориться в пару 0,200 кг води?

7.162. На рис. 7.7 показаний процес переходу системи зі стану 1 в стан 2 трьома різними способами. При якому переході система одержує більшу кількість теплоти? В якому випадку буде більшою зміна ентропії? Рис. 7.7

7.163. Внутрішня енергія тіла зросла на 12,0 Дж, при цьому воно виконало роботу 36,0 Дж. Вважаючи процес ізотермічним і оборотним, визначити зміну ентропії тіла. Температура тіла 300 К.

7.164. Визначити зміну ентропії при охолодженні 200 г води від 100°С до 0°С. Питома теплоємність води 4190 Дж/кг·К.

7.165. Обчислити приріст ентропії при перетворенні 10,0 кг води при 273 К в пару при 373 К.

7.166. Кусок заліза масою 500 г, температура якого була 300 К, нагріли до температури плавлення і розплавили. Визначити зміну ентропії у цьому процесі.

7.167. Обчислити зміну ентропії при змішуванні 4,00 кг води при температурі 290 К та 2,00 кг води при температурі 330 К.

7.168. У калориметр налили 600 г води при температурі 290 К, а потім занурили в неї злиток алюмінію масою 100 г, нагрітий до температури 400 К. Як зміниться ентропія системи після встановлення теплової рівноваги?

7.169. Визначити зміну ентропії 50,0 г льоду при перетворенні його в пару. Початкова температура льоду 230 К, температура пари 373 К.

7.170. Яку масу льоду при температурі 273 К можна перетворити в калориметрі у воду при тій же температурі, якщо ввести 250 г пари при температурі 373 К? Чому дорівнює зміна ентропії системи лід – пара?

7.171. Побудувати діаграму циклу Карно в системі координат „температура - ентропія” і визначити його к.к.д.

7.172. Обчислити зміну ентропії при ізобарному розширенні 6,0 г гелію, якщо об’єм його збільшився в 5разів.

7.173. Тиск 20,0 г вуглекислого газу зменшився від 400 кПа до 200 кПа при сталій температурі. Визначити зміну ентропії газу.

7.174. При ізохорному нагріванні деякої маси двоатомного газу ентропія його зросла на 15 Дж/К. На скільки зросте ентропія цього ж газу, якщо його нагрівати ізобарно в такому ж діапазоні температур?

7.175. Визначити зміну ентропії 1,0 кг кисню, який спочатку ізобарно нагріли так, що його об’єм зріс в 5разів, а потім ізохорно охолодили, щоб зменшити його тиск в 5 разів?

7.176. Тиск 2,0 г азоту змінився від 25 кПа до 10 кПа, а об’єм - від 1,0 л до 5,0 л. Обчислити приріст ентропії газу.

7.177. В одній посудині об’ємом 1,50 л міститься 20,0 г азоту, в іншій посудині об’ємом 2,50 л міститься 25,0 г кисню. Температури газів однакові. На скільки зросте ентропія системи, якщо посудини з’єднують і гази перемішуються?

7.178. В одній половині теплоізольованої посудини знаходиться водень, друга половина відкачана до високого вакууму. Після того як отвір в перегородці відкрили і газ заповнив весь об’єм, його ентропія зросла на 29 Дж/К. Визначити масу газу, вважаючи його ідеальним.

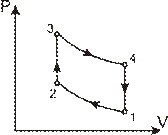
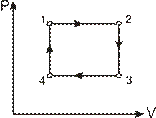7.179. 2 молі ідеального триатомного газу в стані 1 (рис. 7.8) займають об’єм 2.0 л і перебувають під тиском 1,0 МПа, а в стані 3 ці параметри газу становлять відповідно 5,0 л і 0,50 Па. Визначити зміну ентропії газу при переході зі стану 1 в стан 3, якщо перехід відбувається: а) шляхом 1 - 2 - 3; б) шляхом 1 - 4 - 3.

Рис. 7.8

7.180. У теплоізольованій посудині, поділеній перегородкою, міститься ідеальний газ. Температура газу в обох частинах посудини дорівнює 290 К. Об’єм однієї частини посудини 1,0 л, другої - 2,0 л. Тиск газу в першій частині 0,20 МПа, в другій - 0,5 Па. Обчислити зміну ентропії газу після зняття перегородки і встановлення рівноважного стану.

7.181. Як змінюється термодинамічна ймовірність станів в таких процесах: а) при сталому об’ємі зростає внутрішня енергія системи; б) при сталій внутрішній енергії зростає об’єм системи?

7.182. Яку кількість енергії повинна одержати система при сталій температурі 350 К, щоб термодинамічна імовірність її стану збільшилася в 2 рази?

7.183. У скільки разів зростає термодинамічна імовірність стану 1 г льоду, взятого при температурі 273 К, при його перетворенні у воду при тій же температурі?

7.184. Невеличка теплоізольована посудина поділена на дві однакові частини теплонепроникною перегородкою. У кожній частині знаходиться по 1,0 мг азоту. Температура газу в одній частині посудини 295 К, в іншій - 293 К. Визначити, у скільки разів зростає термодинамічна імовірність стану системи при вирівнюванні температур?

7.185. Визначити значення сталих 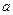і 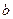у рівнянні стану Ван-дер-Ваальса для повітря. Критичні тиск і температура повітря дорівнюють: 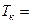132,5 К; 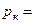37,6·10⁵ Па.

7.186. Визначити критичний тиск і критичну температуру неону. Стал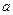і і 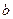в рівнянні Ван-дер-Ваальса для неону відповідно дорівнюють 0,0213 Па·м⁶·моль^-2 та 1,7·10^-5 м³·моль^-1.

7.187. Вуглекислий газ масою 8,8 кг займає об’єм 4.2 м³ під тиском 1,2·10⁵ Па. Визначити температуру газу, користуючись рівняннями Ван-дер-Ваальса і Менделєєва-Клапейрона. Стал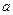і і 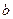для вуглекислого газу відповідно дорівнюють 0,364 Па·м⁶·моль^-2 та 4,3·10^-5 м³·моль^-1.

7.188. Для деякого газу поправка в рівнянні Ван-дер-Ваальса 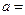0,453 Па·м⁶·моль^-2, а критична температура 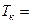282,7 К. Визначити ефективний діаметр молекул газу.