Лекция 5. Радиоактивный распад. Общие закономерности 1 страница

5.1. Сущность явления радиоактивности.Открытие и изучение явления радиоактивного распада явилось первым этапом на пути познания структуры ядра и свойств элементарных частиц. Развитие исследований в этой области проходило в возрастающем темпе, начиная с конца XIX в., и продолжается в настоящее время.

В 1896 г. Анри Беккерель открыл радиоактивность урана (₉₂U). Чуть позже было обнаружено, что радиоактивностью обладают и соединения тория (₉₀Th). В 1898 г. Пьер Кюри и Мария Склодовская-Кюри выделили из урановой руды радий (₈₈Ra) и полоний (₈₄Po), радиоактивность которых оказалась в миллионы раз сильнее радиоактивности урана и тория. Однако природа радиоактивности стала понятной лишь после того, как Резерфорд и Содди показали, что радиоактивность элементов сопровождается их превращением в другие химические элементы (тем самым постулат о неизменяемости атомов был опровергнут).

Явление радиоактивности состоит в самопроизвольном распаде ядра с испусканием одной или нескольких частиц. В результате распада у ядра может измениться как заряд Z, так и массовое число А. Ядра, испытывающие самопроизвольный распад, называют радиоактивными[40], а не испытывающие – стабильными. Тем не менее, такое деление в значительной мере условно, и на практике радиоактивными считаются те ядра, распад которых может быть зарегистрирован существующими на данный момент физическими методами.

Область времен жизни радионуклидов охватывает промежутки времени от сколь угодно больших до заметно превышающих ядерное время τ_я = 10^–22 секунды. Считается, что изменение состава ядра вследствие радиоактивного распада должно происходить не раньше, чем через 10^–12 с после его рождения: за это (очень большое в ядерном масштабе) время проходят все внутриядерные процессы, и ядро успевает полностью сформироваться. Если среднее время жизни ядра меньше, чем 10^–12 с, распад уже не принято считать радиоактивным. Так, при ядерных реакциях[41] образуются короткоживущие агрегаты нуклонов, которые сильно возбуждены и распадаются настолько быстро, что не могут считаться сложившимися атомными ядрами.

Радиоактивный распад характеризуется скоростью его протекания, видом испускаемых частиц и их энергией, а при вылете из ядра нескольких частиц еще и относительными углами между направлениями вылета частиц. Различают следующие основные виды радиоактивного распада: 1) α-распад; 2) β-распад; 3) γ-распад[42]; 4) спонтанное деление. Существуют и некоторые другие виды распада, наблюдающиеся достаточно редко.

При α-распаде ядро испускает α-частицу ( ):

.

Образуется новое ядро, массовое число которого меньше, чем у исходного, на 4 единицы, а заряд – на 2 единицы, т.е. ΔА = –4, ΔZ = –2.

При β-распаде возможен один из трех следующих процессов:

а) испускание электрона и антинейтрино (β^–-распад)

;

б) испускание позитрона и нейтрино (β⁺-распад)

;

в) захват орбитального электрона и испускание нейтрино (электронный захват)

.

Таким образом, в процессах β-распада ΔА = 0, а ΔZ = ±1 (знак «+» соответствует β^–-распаду, а знак «–» β⁺-распаду и электронному захвату).

Изомерный переход – это испускание ядром фотона высокой энергии (γ-кванта):

При этом заряд и массовое число ядра не изменяются, меняется лишь его энергетическое состояние.

Результатом спонтанного деления является образование двух сравнимых по массам осколков и испускание нескольких (двух-трех) нейтронов:[43]

.

Необходимым (но не всегда достаточным) условием радиоактивного распада является энергетическая выгодность: масса распадающегося (материнского) ядра должна превышать сумму масс образующегося (дочернего) ядра и испускаемых частиц:

.

Отсюда следует, что радиоактивный распад – процесс экзотермический, т.е. идет с выделением энергии

. (5.1)

Выделяющаяся энергия Е – это суммарная кинетическая энергия всех продуктов распада. Как уже отмечалось, само по себе условие положительности Е еще не достаточно для того, чтобы ядро претерпевало данный вид распада. Энергетически разрешенный распад может быть запрещен другим законами сохранения: момента импульса, электрического заряда и т.п. С другой стороны, в отсутствие строгого запрета любой энергетически выгодный процесс обязательно будет происходить с той или иной (пусть исчезающее малой) вероятностью.

5.2. Основной закон радиоактивного распада. Активность.Радиоактивный распад является следствием неустойчивости ядра, или, более точно, – его состояния. Повлиять на ход распада, не изменив состояния атомного ядра, нельзя, поэтому на радиоактивный распад не оказывают влияния ни изменение температуры, давления или агрегатного состояния вещества, ни электрические и магнитные поля, ни химические реакции, в которых участвует радионуклид.[44]

Как показывают наблюдения, радиоактивный распад – процесс статистический. Так, например, в одних и тех же условиях за одинаковый промежуток времени можно зарегистрировать несколько распадов, а можно не зарегистрировать ни одного. Однако средняя скорость распада радионуклида, вычисленная по наблюдению очень большого числа распадов отдельных ядер, оказывается постоянной в любых независимых измерениях при любых условиях. В этом случае кинетика распада будет описываться следующим образом. Пусть в некоторый момент времени t имеется ансамбль из N одинаковых радиоактивных ядер. Предположим, что за время dt распадается dN ядер. Величина dN будет пропорциональна промежутку времени dt и числу ядер N:

, (5.2)

где λ – коэффициент пропорциональности, характеризующий среднюю скорость распада данного радионуклида и называемый постоянной распада. Знак минус означает, что с течением времени число нераспавшихся ядер уменьшается. Разделив переменные и проинтегрировав, получаем:

, (5.3)

где N₀ – число радиоактивных ядер при t = 0. Равенство (5.3) носит название основного закона радиоактивного распада.

Постоянную распада λ можно связать со средним временем жизни радиоактивного ядра τ. Для этого изобразим кривую радиоактивного распада в координатах N/N₀ – t (рис. 5.1). В соответствии с математическим определением среднего значения функции (в интервале от 0 до 1),

.

Учитывая, что значение интеграла равно площади S (заштрихована на рис. 5.1), а также то, что площадь не зависит от способа ее вычисления, имеем:

.

Используя (5.3), находим значение последнего интеграла:

.

Таким образом, среднее время жизни ядра

. (5.4)

В качестве характеристики скорости распада радионуклида на практике чаще используют другую величину – период полураспада Т_1/2. Это время, в течение которого количество ядер уменьшается в два раза. Между периодом полураспада и постоянной распада также существует простая зависимость: из (5.3) после подстановки N = N₀/2 и логарифмирования получаем

(5.5)

Подчеркнем еще раз, что постоянная распада λ – величина, не зависящая от времени, поскольку различные моменты времени ничем не выделены друг перед другом с точки зрения предстоящего распада ядра. В силу этого для радиоактивных ядер не существует понятия возраста: они не «стареют и не портятся». Получаемые в реакторах и ускорителях радионуклиды распадаются с той же средней скоростью, что и те же радионуклиды природного происхождения, образовавшиеся много лет назад. Именно поэтому период полураспада может использоваться для идентификации радионуклидов. Однако прежде чем перейти к методам измерения Т_1/2, введем еще одно важное определение.

На практике часто приходится иметь дело с такими малыми количествами радионуклидов, когда привычные единицы измерения массы или количества вещества (грамм, моль и т.п.) оказываются более чем избыточными. С другой стороны, для определения количества радионуклида чаще всего используется регистрация испускаемого им излучения (α-, β-, γ-, нейтронов и т.п.). Поэтому целесообразнее характеризовать это количество единицами активности, т.е. числом ядер n, распадающихся за единицу времени. Активность радионуклида связана с количеством его ядер следующим образом:

. (5.6)

За единицу активности в системе СИ принимается один распад в секунду, или один беккерель (Бк). Часто используется и внесистемная единица – кюри (Ки). 1 Ки – активность такого радиоактивного образца, в котором за 1 секунду происходит 3,7·10¹⁰ распадов (1 Ки = 3,7·10¹⁰ Бк). Исторически своим появлением последняя единица обязана открытию радия: один кюри приблизительно соответствует активности одного грамма изотопа ²²⁶Ra.

Экспериментальное определение периода полураспада (постоянной распада) радионуклида осуществляют, используя детекторы излучения ядер. Зная количество ядер N и измерив с помощью детектора активность А, можно определить постоянную распада из равенства (5.6). Такой метод абсолютного счета пригоден для долгоживущих радионуклидов, активность которых в течение эксперимента (в том числе, по определению N) практически не изменяется. В противном случае используется метод прямого определения. Число частиц (α-, β-, γ-квантов, нейтронов), регистрируемых детектором за малые промежутки времени, пропорционально активности на момент измерения. В свою очередь,

. (5.7)

Таким образом, график зависимости скорости счета частиц детектором в полулогарифмических координатах – прямая, угловой коэффициент которой есть постоянная распада λ.

Метод прямого определения используют, когда период полураспада лежит в пределах от нескольких минут до нескольких дней или недель. Для более короткоживущих радионуклидов трудности, связанные с определением времени, прошедшего с начала эксперимента, в настоящее время помогают преодолеть электронные схемы, включающие и выключающие детектор через короткие и строго фиксированные промежутки времени.

5.3. Статистический характер радиоактивного распада.Как отмечалось выше, закон уменьшения числа радиоактивных ядер выполняется статистически, т.е. тем точнее, чем больше их количество. Отдельные же распады происходят совершенно случайно: предсказать, в какой момент времени распадется то или другое ядро, невозможно. Таким образом, количество распадов в единицу времени представляет собой случайную величину. В данном разделе мы найдем вид распределения этой случайной величины и установим, насколько велики могут быть отклонения скорости распада от среднего значения.

Рассмотрим распад в ансамбле из N₀ радиоактивных ядер в течение времени t. Ядра ансамбля можно разбить на две группы. В первую войдут те ядра, которые распадутся за время t, во вторую – те, которые не распадутся за это время. Вероятность распада одного ядра p = 1 – q. Тогда вероятность такого сложного события, когда по истечении времени t распадутся n ядер из N₀, будет равна

, (5.8)

где – вероятность распада n ядер первой группы, – вероятность того, что ядер второй группы при этом не распадутся,

(5.9)

– число способов выбрать n ядер из общего числа N₀. Зависимость W(n) вероятности случайного события от количественной характеристики n в полученном нами виде носит название биномиального распределения дискретной случайной величины, поскольку может быть представлена как один из членов разложения бинома Ньютона:

(из последнего равенства видно, что сумма вероятностей всех возможных событий равна единице). Можно показать (см. ПРИЛОЖЕНИЕ Г), что для биномиального распределения среднее значение[45]

. (5.10)

Реальное количество распадов, являясь случайной величиной, всегда более или менее отличается от среднего. Для оценки разброса значений случайной величины используется дисперсия D, определяемая как средний квадрат отклонения от среднего значения:

.

Для биномиального распределения

. (5.11)

Закон биномиального распределения можно упростить, если выполняются следующие условия: n << N₀ и р << 1, т.е. если начальное количество ядер велико, а распадаются они не слишком часто. В этом случае биномиальное распределение переходит в распределение Пуассона

. (5.12)

В отличие от биномиального распределения (5.8), характеризующегося двумя параметрами (N₀ и р), оно содержит только один параметр . Эксперименты по определению истинного числа распадов в единицу времени дают результаты, хорошо согласующиеся с таким распределением. Дисперсия случайной величины, распределенной по закону Пуассона,

. (5.13)

Данный результат следует непосредственно из (5.11), если р << 1.

Распределение Пуассона определено для целочисленных значений n. При этом через соответствующие точки можно провести плавную кривую. Для малых значений получается несимметричная кривая. По мере увеличения , а значит, и числа точек, кривая становится все более симметричной, причем ее максимум приходится на (рис. 5.2). Таким образом, при 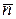>> 1 число распадов можно рассматривать как непрерывную случайную величину, распределенную нормально, или по закону Гаусса:

. (5.14)

Дисперсия нормального распределения (5.14) связана со средним значением так же, как и в распределении Пуассона: .[46]

Вывод среднего и дисперсии биномиального распределения, а также связь между тремя распределениями даны в ПРИЛОЖЕНИИ Г.

Для определения доверительного интервала нормально распределенной величины n используют следующее выражение:

,

где k_P – квантиль нормального распределения, соответствующий выбранной доверительной вероятности Р. На практике при обработке экспериментальных данных часто пользуются стандартным отклонением Δn, для которого k_P = 1, а Р ≈ 0,683 (т.е. среднее число распадов с вероятностью 68,3% отличается от экспериментально полученного не более чем на ). Величина

представляет собой относительную ошибку измерения. Если в эксперименте зарегистрировано достаточно большое число распадов, то для определения ошибки вместо неизвестного среднего можно использовать само значение n. Так как , относительная ошибка

. (5.15)

Отсюда следует, что для достижения заданного уровня точности измерения необходимо зарегистрировать 1/r² распадов (например, для измерения с 1%-ной ошибкой n должно быть равно 10⁴).

Лекция 6. Радиоактивный распад. Общие закономерности (окончание)

6.1. Сложный распад. Последовательные и параллельные превращения.Обратимся теперь вновь к эксперименту по определению периода полураспада радионуклида. Статистический характер радиоактивного распада приводит к тому, что в реальных измерениях активности со сколь угодно совершенной аппаратурой экспериментальные точки, нанесенные на график в координатах lnA – t, всегда будут иметь разброс по обе стороны прямой, проведенной по методу наименьших квадратов. При этом следует убедиться, что стандартное отклонение не превышает , т.е. прямая лежит внутри доверительного интервала, определенного для каждой из точек. Если провести прямую не получается (рис. 6.1), то аппаратурой регистрируется более сложное явление, чем простой распад ядер одного и того же сорта.[47] Рассмотрим различные виды сложного распада.

Во-первых, сложный распад может быть обусловлен тем, что исследуемое вещество содержит не один, а несколько различных радионуклидов. Тогда зависимость активности от времени будет выглядеть следующим образом:

,

где – активность i-го радионуклида в начальный момент времени. В случае смеси двух радионуклидов

. (6.1)

Если периоды полураспада радионуклидов различаются достаточно сильно (λ₁ >> λ₂), то при малых t показатель экспоненты при А₀₂ близок к нулю. Тогда

.

При больших t можно пренебречь первым слагаемым под логарифмом в (6.1):

.

Таким образом, постоянные λ₁ и λ₂ определяются по угловым коэффициентам касательной к графику в точке t = 0 и асимптоты при (рис. 6.1).

Во-вторых, в результате распада материнского ядра Э₁ образующееся дочернее ядро Э₂ может также оказаться радиоактивным. В этом случае мы имеем дело с последовательностью радиоактивных превращений, например

Э₁ (l₁) → Э₂ (l₂) → Э₃ (l₃) → …

Количество дочерних ядер каждого вида как функция времени определяется, с одной стороны, скоростью их распада и, с другой стороны, скоростью их образования, равной скорости распада соответствующих материнских ядер. Тогда, в соответствии с (5.2), получаем следующую систему дифференциальных уравнений:

,

, (6.2)

и т.д. Ее решение[48] для простейшего случая двух последовательных распадов при начальных условиях и имеет вид:

,

. (6.3)

Отметим, что первое слагаемое в (6.3) описывает изменение во времени числа дочерних ядер, уже существовавших к начальному моменту времени. Если (дочернего радионуклида еще нет), то суммарная активность будет определяться следующим выражением:

. (6.4)

Рассмотрим далее два практически важных предельных случая.

A. Пусть материнский радионуклид является короткоживущим по сравнению с долгоживущим дочерним, т.е. λ₁ >> λ₂. Тогда из (6.4) получим

.

Это выражение по своему виду аналогично (6.1). Следовательно, зависимость активности от времени будет в этом случае выглядеть так же, как это изображено на рис. 6.1: материнский радионуклид очень быстро распадается, и долгоживущая активность определяется скоростью распада дочернего радионуклида.

B. Наибольший интерес представляет противоположный случай, когда дочерний радионуклид является короткоживущим по сравнению с долгоживущим материнским, т.е. когда λ₂ > λ₁. Из (6.3) найдем, что

. (6.5)

Логарифм суммарной активности выразится тогда как

.

Значение экспоненты во втором слагаемом быстро стремится к нулю, поэтому на начальном отрезке времени активность быстро увеличивается, а затем медленно спадает в соответствии с изменением А₁ (рис. 6.2).

Если время, прошедшее с момента t = 0, в несколько раз превышает период полураспада дочерних ядер, то

, (6.6)

т.е. активности материнского и дочернего радионуклидов в любой момент времени равны с точностью до постоянного множителя λ₂/(λ₂ – λ₁).

lnA

Соотношение (6.6) выражает закон радиоактивного равновесия.[49] При активности материнского и дочернего радионуклидов практически равны: А₂ = А₁. Если при этом рассматриваемый промежуток времени настолько мал по сравнению с периодом полураспада материнского радионуклида, что изменением его активности со временем можно пренебречь, говорят о вековом равновесии (в противном случае равновесие называют подвижным). В состоянии векового равновесия скорость распада дочерних ядер равна скорости их образования за счет распада материнских, т.е. dN₂/dt = 0 и N₂ = const.

Наконец, рассмотрим случай, когда одни и те же ядра испытывают несколько видов радиоактивных превращений (примерами могут служить конкуренция α- и β^–-распада у тяжелых ядер, β^–- и β⁺-распада у нечетно-нечетных ядер, образование различных ядерных изомеров и т.д.).[50] Существенно то, что каждое превращение характеризуется собственной постоянной распада, определяющей его вероятность.

Пусть ядро Э₁ способно превращаться в одно из ядер Э_i. Уравнение для скорости распада будет тогда выглядеть как

,

т.е. постоянная распада λ₁ есть сумма постоянных λ_1i по всем возможным видам, или каналам распада. Если, в свою очередь, Э_i – радиоактивное ядро, то

.

Величину

(6.8)

называют выходом i-го продукта превращения. Очевидно, что суммарный выход по всем каналам (как полная вероятность превращения)

.

6.2. Радиоактивные цепочки.Параллельные и последовательные превращения радиоактивных ядер нередко приводят к достаточно сложным радиоактивным цепочкам, например

Э₁(l₁) → Э₂(l₂) → Э₃(l₃) → Э₅(l₅) →…→ Э_n(l_n) →….

Э₄(l₄) → Э₆(l₆)

Как было показано Г. Бейтманом (1910 г.), для неразветвленной цепочки, состоящей из двух и более звеньев, когда при t = 0 имеется только радионуклид Э₁, число ядер n-го радионуклида

. (6.9)

В том случае, когда требуется общее решение при N₀₂, N₀₃,… ≠ 0, его можно получить путем добавления к (6.9) аналогичных решений для более коротких цепочек, начинающихся с Э₂, Э₃ и т.д.